 排序
排序
# 排序
# 选择排序
public static void selectionSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
// 0 ~ N-1 找到最小值,在哪,放到0位置上
// 1 ~ n-1 找到最小值,在哪,放到1 位置上
// 2 ~ n-1 找到最小值,在哪,放到2 位置上
for (int i = 0; i < arr.length - 1; i++) {
int minIndex = i;
for (int j = i + 1; j < arr.length; j++) { // i ~ N-1 上找最小值的下标
minIndex = arr[j] < arr[minIndex] ? j : minIndex;
}
swap(arr, i, minIndex);
}
}
public static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# 冒泡排序
public static void bubbleSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
// 0 ~ N-1
// 0 ~ N-2
// 0 ~ N-3
for (int e = arr.length - 1; e > 0; e--) { // 0 ~ e
for (int i = 0; i < e; i++) {
if (arr[i] > arr[i + 1]) {
swap(arr, i, i + 1);
}
}
}
}
// 交换arr的i和j位置上的值
public static void swap(int[] arr, int i, int j) {
arr[i] = arr[i] ^ arr[j];
arr[j] = arr[i] ^ arr[j];
arr[i] = arr[i] ^ arr[j];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# 插入排序
public static void insertionSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
// 不只1个数
for (int i = 1; i < arr.length; i++) { // 0 ~ i 做到有序
for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1]; j--) {
swap(arr, j, j + 1);
}
}
}
// i和j是一个位置的话,会出错
public static void swap(int[] arr, int i, int j) {
arr[i] = arr[i] ^ arr[j];
arr[j] = arr[i] ^ arr[j];
arr[i] = arr[i] ^ arr[j];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 归并排序
该算法是采用分治法的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
public static void mergeSort1(int[] arr) {
if (arr == null || arr.length < 2) { // 为空 或 小于两个元素无法排序
return;
}
process(arr, 0, arr.length - 1);
}
public static void process(int[] arr, int l, int r) {
if (l == r) { // 只有一个元素
return;
}
int mid = l + ((r - l) / 2); // 为了防止越界 相当于(l+r)/2
process(arr, l, mid); // 递归分治
process(arr, mid + 1, r); // 递归
merge(arr, l, mid, r); // 合并子序列
}
public static void merge(int[] arr, int l, int m, int r) {
int[] prearr = new int[r - l + 1]; // 开辟存储排序好的数组 左右组有多少个元素就开辟多少个位置
int index = 0; // 存储数组指针
int p1 = l; // 左组指针
int p2 = m + 1; // 右组指针
while (p1 <= m && p2 <= r) { // 防止左右指针越界
prearr[index++] = arr[p1] <= arr[p2] ? arr[p1++] : arr[p2++]; // 比较大小
}
while (p1 <= m) { // 左指针未越界
prearr[index++] = arr[p1++];
}
while (p2 <= r) { // 右指针未越界
prearr[index++] = arr[p2++];
}
// 归并到原始数组
for (int i = 0; i < prearr.length; i++) {
arr[l + i] = prearr[i];
}
}
//非递归
public static void mergeSort2(int[] arr) {
if (arr == null || arr.length < 2) { // 为空或小于2个元素
return;
}
int step = 1; // 步长为 1 2 4 8 16 32 2的次方(即多少个为一组)
int N = arr.length; // 长度
while (step < N) { // 如果步长 超过 长度
int L = 0; // 左指针
while (L < N) {
int M = 0; // 右指针重置
if (N - L >= step) { // 右指针到左指针 大于等于步长
M = L + step - 1; // 右指针赋值
} else {
M = N - 1; // 否则右指针为 数组长度-1 为了赋值数值溢出
}
if (M == N - 1) { // 如果左组的 右指针为数组中最后一个则 无右组比较 直接break
break;
}
int R = 0; // 右组右指针
if (N - 1 - M >= step) { // 右组是否能凑齐step个元素
R = M + step;
} else { // 无法凑齐 右指针到数组尾元素
R = N - 1;
}
merge(arr, L, M, R); // 合并区间 L为左组左指针 M为左组右指针 M+1为右组左指针 R为右组右指针
if (R == N - 1) { // 右组右指针到数组尾 结束本次步长
break;
} else { // 否则重新赋值左组左指针 进行一个大组的区间合并
L = R + 1;
}
}
if (step > N / 2) { // 当前步长不能凑齐左右两组 进行合并区间
break;
}
step *= 2; // 步长增加
}
}
// 非递归方法实现
public static void mergeSort3(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
int N = arr.length;
int mergeSize = 1;
while (mergeSize < N) {
int L = 0;
while (L < N) {
if (mergeSize >= N - L) { //当前步长大于剩下为合并的元素
break;
}
int M = L + mergeSize - 1; //左组右指针
int R = M + Math.min(mergeSize, N - M - 1); //右组右指针
merge(arr, L, M, R);
L = R + 1;
}
if (mergeSize > N / 2) {
break;
}
mergeSize <<= 1;
}
}
// for test
public static int[] generateRandomArray(int maxSize, int maxValue) {
int[] arr = new int[(int) ((maxSize + 1) * Math.random())];
for (int i = 0; i < arr.length; i++) {
arr[i] = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
}
return arr;
}
// for test
public static int[] copyArray(int[] arr) {
if (arr == null) {
return null;
}
int[] res = new int[arr.length];
for (int i = 0; i < arr.length; i++) {
res[i] = arr[i];
}
return res;
}
// for test
public static boolean isEqual(int[] arr1, int[] arr2) {
if ((arr1 == null && arr2 != null) || (arr1 != null && arr2 == null)) {
return false;
}
if (arr1 == null && arr2 == null) {
return true;
}
if (arr1.length != arr2.length) {
return false;
}
for (int i = 0; i < arr1.length; i++) {
if (arr1[i] != arr2[i]) {
return false;
}
}
return true;
}
// for test
public static void printArray(int[] arr) {
if (arr == null) {
return;
}
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
System.out.println();
}
// 对数器
public static void main(String[] args) {
int testTime = 500000;
int maxSize = 100;
int maxValue = 100;
System.out.println("测试开始");
for (int i = 0; i < testTime; i++) {
int[] arr1 = generateRandomArray(maxSize, maxValue);
int[] arr2 = copyArray(arr1);
mergeSort1(arr1);
mergeSort2(arr2);
if (!isEqual(arr1, arr2)) {
System.out.println("出错了!");
printArray(arr1);
printArray(arr2);
break;
}
}
System.out.println("测试结束");
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
# 求数组小和
给一个数组 arr [L-R] 范围既要排好序,也要返回每个元素在排序前比当前元素小的和
public static int smallSum(int[] arr) {
if (arr == null || arr.length < 2) {
return 0;
}
return process(arr, 0, arr.length - 1);
}
private static int process(int[] arr, int l, int r) {
if (l == r) {
return 0;
}
int mid = l + ((r - l) >> 1);
return process(arr, l, mid) + process(arr, mid + 1, r) + merge(arr, l, mid, r);
}
private static int merge(int[] arr, int l, int mid, int r) {
int[] arr2 = new int[r - l + 1];
int i = 0;
int p1 = l;
int p2 = mid + 1;
int ans = 0; // 当前归并最小和
while (p1 <= mid && p2 <= r) {
ans += arr[p1] < arr[p2] ? arr[p1] * (r - p2 + 1) : 0; // 如果先放入左组 则代表有r-p2+1个元素大于当前左组的元素 否则没有最小
arr2[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++]; // 比较大小归并 如等于先放右组避免将相同值元素统计到r-p2+1中
}
while (p1 <= mid) {
arr2[i++] = arr[p1++];
}
while (p2 <= r) {
arr2[i++] = arr[p2++];
}
for (i = 0; i < arr2.length; i++) {
arr[l + i] = arr2[i];
}
return ans;
}
// for test
public static int comparator(int[] arr) {
if (arr == null || arr.length < 2) {
return 0;
}
int res = 0;
for (int i = 1; i < arr.length; i++) {
for (int j = 0; j < i; j++) {
res += arr[j] < arr[i] ? arr[j] : 0;
}
}
return res;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
# 求数组中的逆序对数量
给定一个数组 arr,求数组的降序对总数量
在一个数组中,任何一个前面的数 a,和任何一个后面的数 b,如果 (a,b) 是降序的,就称为降序对
public static int reverPairNumber(int[] arr) {
if (arr == null || arr.length == 0) {
return 0;
}
return prcess(arr, 0, arr.length - 1);
}
public static int prcess(int[] arr, int l, int r) {
if (l == r) {
return 0;
}
int m = l + ((r - l) >> 1);
return prcess(arr, l, m) + prcess(arr, m + 1, r) + merge(arr, l, m, r);
}
public static int merge(int[] arr, int l, int m, int r) {
int ans = 0;
int[] help = new int[r - l + 1];
// 倒着遍历
int i = help.length - 1; // 从尾部开始
int p1 = m; // 左边边界
int p2 = r; // 右组边界
while (p1 >= l && p2 > m) {
ans += arr[p1] > arr[p2] ? (p2 - m) : 0; // 如果左边指针数大于右边指针数则为降序对
help[i--] = arr[p1] > arr[p2] ? arr[p1--] : arr[p2--];
}
while (p1 >= l) {
help[i--] = arr[p1--];
}
while (p2 > m) { // 注意到m就停止
help[i--] = arr[p2--];
}
for (int j = 0; j < help.length; j++) {
arr[l + j] = help[j];
}
return ans;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
# 493. 翻转对 (opens new window)
在一个数组中,对于任何一个数 num,求有多少个 (后面的数 * 2) 依然 < num,返回总个数
比如:[3,1,7,0,2]
3的后面有:1,0
1的后面有:0
7的后面有:0,2
0的后面没有
2的后面没有
所以总共有5个
1
2
3
4
5
6
7
2
3
4
5
6
7
# 327. 区间和的个数 (opens new window)
public int countRangeSum(int[] nums, int lower, int upper) {
if (nums == null || nums.length == 0) {
return 0;
}
// 前缀和数组
long[] sum = new long[nums.length];
sum[0] = nums[0];
for (int i = 1; i < nums.length; i++) {
sum[i] = sum[i - 1] + nums[i];
}
// 原数组 已无用 传递前缀和数组
return process(sum, 0, nums.length - 1, lower, upper);
}
private int process(long[] sum, int l, int r, int lower, int upper) {
if (l == r) {
// 只有一个数时 判断是否在lower和upper范围内 是则res+1
return sum[l] >= lower && sum[l] <= upper ? 1 : 0;
}
int m = l + ((r - l) >> 1);
// 递归+合并
return process(sum, l, m, lower, upper) + process(sum, m + 1, r, lower, upper)
+ merge(sum, l, m, r, lower, upper);
}
private int merge(long[] sum, int l, int m, int r, int lower, int upper) {
int ans = 0;
int windowL = l;
int windowR = l; // [windowL, windowR)
for (int i = m + 1; i <= r; i++) { // 从右组开始遍历
long min = sum[i] - upper;
long max = sum[i] - lower;
while (windowR <= m && sum[windowR] <= max) {
windowR++; // 找到最大值下标边界
}
while (windowL <= m && sum[windowL] < min) {
windowL++; // 最小值下标边界
}
ans += windowR - windowL; // 右组当前元素有多少个在范围内的
}
//归并
long[] help = new long[r - l + 1];
int i = 0;
int p1 = l;
int p2 = m + 1;
while (p1 <= m && p2 <= r) {
help[i++] = sum[p1] <= sum[p2] ? sum[p1++] : sum[p2++];
}
while (p1 <= m) {
help[i++] = sum[p1++];
}
while (p2 <= r) {
help[i++] = sum[p2++];
}
for (int j = 0; j < help.length; j++) {
sum[l + j] = help[j];
}
return ans;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
# 快速排序
// 递归经典写法
public static void QuickSort(int[] arr, int l, int r) {
if (l >= r) {
return;
}
int left = l;
int right = r;
int base = arr[r]; // 以最后一个为基准 如果以头为基准则应该先找大于基准 再找小于基准的
while (left < right) {
// 将小于等于base的放到左边 则应该left++
while (arr[left] <= base && left < right) {
left++;
}
// 将大于等于base的放到右边 则right--
while (arr[right] >= base && left < right) {
right--;
}
if (left < right) {
// 交换
int temp = arr[left];
arr[left] = arr[right];
arr[right] = temp;
}
}
arr[r] = arr[left]; // 将小于基准的最后一个数 交换到base位置
arr[left] = base; // 将base值 交换到小于基准的位置
// 拆分大问题 递归
QuickSort(arr, l, left - 1);
QuickSort(arr, right + 1, r);
}
public static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
# 荷兰国旗问题
荷兰国旗是由红白蓝 3 种颜色的条纹拼接而成,把这些条纹按照颜色排好,红色的在上半部分,白色的在中间部分,蓝色的在下半部分,我们把这类问题称作荷兰国旗问题。
其核心思想为 分区 小于基准放左边 等于基准的放中间 大于基准的放右边
public static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
// arr[L...R] 玩荷兰国旗问题的划分,以arr[R]做划分值
// <arr[R] ==arr[R] > arr[R]
public static int[] netherlandsFlag(int[] arr, int L, int R) {
if (L > R) { // L...R L>R
return new int[] { -1, -1 };
}
if (L == R) {
return new int[] { L, R };
}
int less = L - 1; // < 区 右边界
int more = R; // > 区 左边界
int index = L;
while (index < more) { // 当前位置,不能和 >区的左边界撞上
if (arr[index] == arr[R]) {
index++;
} else if (arr[index] < arr[R]) {
// swap(arr, less + 1, index);
// less++;
// index++;
swap(arr, index++, ++less);
} else { // >
swap(arr, index, --more);
}
}
swap(arr, more, R); // <[R] =[R] >[R]
return new int[] { less + 1, more }; //返回的是等于区的开始节点与结束节点
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# 快排 1.0
1.0 效率低下 每次是最差情况 只将基准放置在排序后的位置 O (N^2)
public static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
// arr[L..R]上,以arr[R]位置的数做划分值
// <= X > X
// <= X X
public static int partition(int[] arr, int L, int R) {
if (L > R) {
return -1;
}
if (L == R) {
return L;
}
int lessEqual = L - 1;
int index = L;
while (index < R) {
if (arr[index] <= arr[R]) { //此为小于等于基准
swap(arr, index, ++lessEqual);
}
index++;
}
swap(arr, ++lessEqual, R);
return lessEqual; //返回小于等于区的边界下标(即大小-1)
}
public static void process1(int[] arr, int L, int R) {
if (L >= R) {
return;
}
// L..R partition arr[R] [ <=arr[R] arr[R] >arr[R] ]
//只有两个区 小于等于区 和 大于区
//1.0效率低下 每次是最差情况 只将基准放置在排序后的位置 O(N^2)
int M = partition(arr, L, R);
process1(arr, L, M - 1);
process1(arr, M + 1, R);
}
public static void quickSort1(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
process1(arr, 0, arr.length - 1);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
# 快排 2.0
2.0 优化每次排序 等于区的数,但最差情况仍有可能每次选中的基准只有 1 个(不重复)
public static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
// arr[L...R] 玩荷兰国旗问题的划分,以arr[R]做划分值
// <arr[R] ==arr[R] > arr[R]
public static int[] netherlandsFlag(int[] arr, int L, int R) {
if (L > R) { // L...R L>R
return new int[] { -1, -1 };
}
if (L == R) {
return new int[] { L, R };
}
int less = L - 1; // < 区 右边界
int more = R; // > 区 左边界
int index = L;
while (index < more) { // 当前位置,不能和 >区的左边界撞上
if (arr[index] == arr[R]) {
index++;
} else if (arr[index] < arr[R]) {
// swap(arr, less + 1, index);
// less++;
// index++;
swap(arr, index++, ++less);
} else { // >
swap(arr, index, --more);
}
}
swap(arr, more, R); // <[R] =[R] >[R]
return new int[] { less + 1, more }; //返回的是等于区的开始节点与结束节点
}
// arr[L...R] 排有序,快排2.0方式
public static void process2(int[] arr, int L, int R) {
if (L >= R) {
return;
}
// [ equalArea[0] , equalArea[0]]
int[] equalArea = netherlandsFlag(arr, L, R);
process2(arr, L, equalArea[0] - 1);
process2(arr, equalArea[1] + 1, R);
}
public static void quickSort2(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
process2(arr, 0, arr.length - 1);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
# 随机快排 3.0
由于我们选择基准是最右的数,有可能会出现最差情况,即每次以右为基准时等于区只有它自身,我们可以在进行分区操作时 在 l 到 r 范围内 随机抽取一个数与 r 位置 (基准位置) 作交换,避免了每次命中最差情况。
public static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
// arr[L...R] 玩荷兰国旗问题的划分,以arr[R]做划分值
// <arr[R] ==arr[R] > arr[R]
public static int[] netherlandsFlag(int[] arr, int L, int R) {
if (L > R) { // L...R L>R
return new int[] { -1, -1 };
}
if (L == R) {
return new int[] { L, R };
}
int less = L - 1; // < 区 右边界
int more = R; // > 区 左边界
int index = L;
while (index < more) { // 当前位置,不能和 >区的左边界撞上
if (arr[index] == arr[R]) {
index++;
} else if (arr[index] < arr[R]) {
// swap(arr, less + 1, index);
// less++;
// index++;
swap(arr, index++, ++less);
} else { // >
swap(arr, index, --more);
}
}
swap(arr, more, R); // <[R] =[R] >[R]
return new int[] { less + 1, more }; //返回的是等于区的开始节点与结束节点
}
public static void process3(int[] arr, int L, int R) {
if (L >= R) {
return;
}
swap(arr, L + (int) (Math.random() * (R - L + 1)), R);//在l到r范围内随机选一个数 交换到r位置,避免多次命中最差情况
int[] equalArea = netherlandsFlag(arr, L, R);
process3(arr, L, equalArea[0] - 1);
process3(arr, equalArea[1] + 1, R);
}
public static void quickSort3(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
process3(arr, 0, arr.length - 1);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
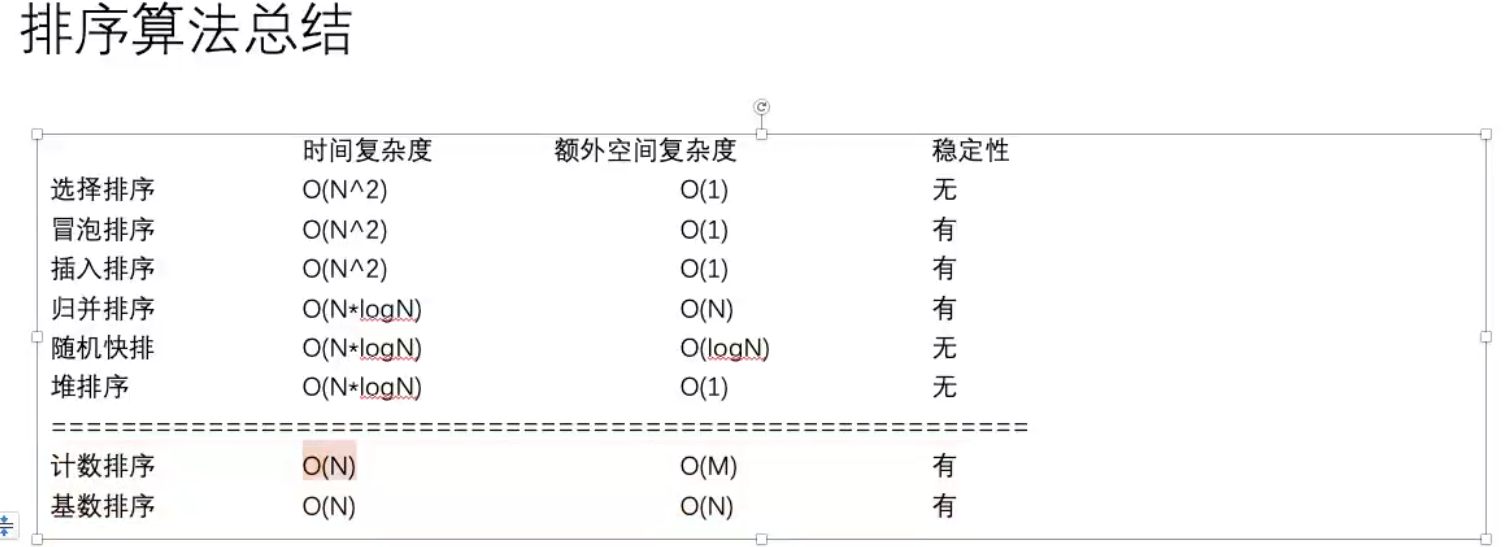
# 排序稳定性
稳定性指是同样大小的样本 再次进行排序之后不会改变相对次序
对于基础类型来说 稳定性没有意义
对于非基础类型来说 稳定性有重要的意义
有的排序算法可以实现成稳定的 而有的排序算法无论如何都实现不成稳定
编辑 (opens new window)
上次更新: 2023/12/06, 01:31:48
