图

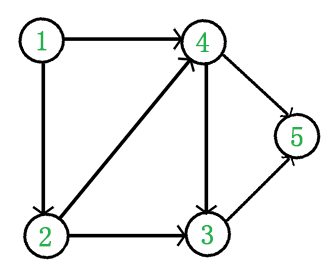
1. 由点的集合和边的集合构成
2. 虽然存在有向图和无向图的概念，但实际上都可以用有向图来表达
3. 边上可能带有权值

BFS

宽度优先遍历，使用队列来进行层的遍历。

1. 利用队列实现
2. 从源节点开始依次按宽度进队列，然后弹出
3. 每弹出一个点，把该节点所有没有进过队列的邻接电放入队列
4. 直到队列变空

	public static void bfs(Node node) {
		if (node == null) {
			return;
		}
		LinkedList<Node> queue = new LinkedList<>();
		HashSet<Node> set = new HashSet<>(); // 防止元素多次进入队列
		queue.add(node);
		set.add(node);
		while (!queue.isEmpty()) {
			Node cur = queue.poll();
			System.out.println(cur);
			for (Node next : cur.nexts) {
				// 如果当前元素没有进入过队列
				if (!set.contains(node)) {
					set.add(next);
					queue.add(next);
				}
			}
		}
	}

DFS

深度优先遍历，使用栈来进行深度遍历，我们可以使用递归来进行编码

1. 利用栈实现
2. 从源节点开始把节点按照深度放入栈，然后弹出
3. 每弹出一个点，把该节点下一个没有进过栈的邻接点放入栈
4. 直到栈变空

	public static void dfs(Node node) {
		if (node == null) {
			return;
		}

		Stack<Node> stack = new Stack<>();
		HashSet<Node> set = new HashSet<>();
		stack.add(node);
		set.add(node);
		System.out.println(node.vaule);
		while (!stack.isEmpty()) {
			Node cur = stack.pop();
			for (Node next : cur.nexts) {
				// 当前子元素没有入过栈
				if (!set.contains(next)) {
					stack.push(cur); // 将根元素重新入栈
					stack.push(next); // 子元素同样入栈
					set.add(next); // 标记为入过栈
					System.out.println(next.vaule); // 输出当前子元素值
					break; // 结束当前根节点的子元素遍历
				}
			}
		}
	}

图的拓扑排序

拓扑排序是对一个有向图构造拓扑序列，** 解决工程是否能顺利进行的问题。** 构造时有 2 种结果：

1. 此图全部顶点被输出：说明说明图中无「环」存在， 是 AOV 网
2. 没有输出全部顶点：说明图中有「环」存在，不是 AOV 网

AOV（Activity On Vertex Network） ：一种 有向 无回路 的图

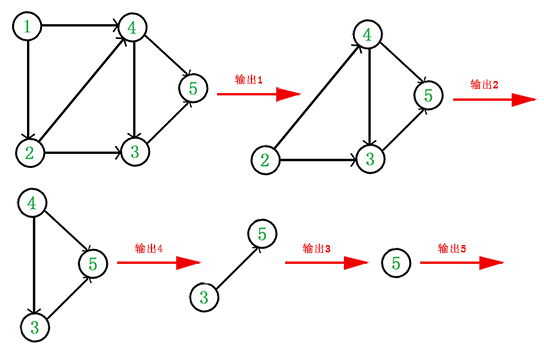
如下面的 DAG 图

1. 从 DAG 图中选择一个 没有前驱（即入度为 0）的顶点并输出。
2. 从图中删除该顶点和所有以它为起点的有向边。
3. 重复 1 和 2 直到当前的 DAG 图为空或当前图中不存在无前驱的顶点为止。后一种情况说明有向图中必然存在环。

于是，得到拓扑排序后的结果是 {1, 2, 4, 3, 5}。

通常，一个有向无环图可以有一个或多个拓扑排序序列。

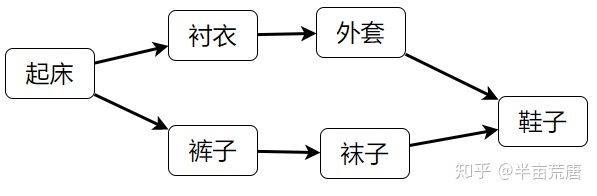
拓扑排序常用来确定一个依赖关系集中，事物发生的顺序。例如，在日常工作中，可能会将项目拆分成 A、B、C、D 四个子部分来完成，但 A 依赖于 B 和 D，C 依赖于 D。为了计算这个项目进行的顺序，可对这个关系集进行拓扑排序，得出一个线性的序列，则排在前面的任务就是需要先完成的任务。 注意：这里得到的排序并不是唯一的！就好像你早上穿衣服可以先穿上衣也可以先穿裤子，只要里面的衣服在外面的衣服之前穿就行。

如果当前节点入度为则说明此节点是首次读取，入栈并存储到结果集合中

public class Node {
		public int value;
		public int in; // 入度
		public int out; // 出度
		public ArrayList<Node> nexts; // 当前节点出发有哪些邻居节点
		public ArrayList<Edge> edges; // 从当前节点出发有哪些边

		public Node(int value) {
			this.value = value;
			in = 0;
			out = 0;
			nexts = new ArrayList<>();
			edges = new ArrayList<>();
		}
	}

	public class Edge {
		public int weight; // 权重
		public Node from; // 父节点
		public Node to; // 子节点

		public Edge(int weight, Node from, Node to) {
			this.weight = weight;
			this.from = from;
			this.to = to;
		}

	}

	public class Graph {
		public HashMap<Integer, Node> nodes;// key存储为value value存储为Node节点
		public HashSet<Edge> edges;

		public Graph() {
			nodes = new HashMap<>();
			edges = new HashSet<>();
		}
	}

	public static List<Node> sortedTopology(Graph graph) {
		// key为节点 value为剩下的入度
		HashMap<Node, Integer> inMap = new HashMap<>();
		// 只有剩下入度为0的点,才进入队列中
		LinkedList<Node> queuq = new LinkedList<>();
		for (Node node : graph.nodes.values()) {
			inMap.put(node, node.in); // 存储每个节点的入度
			if (node.in == 0) {
				// 入队列
				queuq.add(node);
			}
		}
		List<Node> result = new ArrayList<>();
		while (!queuq.isEmpty()) {
			Node cur = queuq.poll();
			result.add(cur);
			for (Node node : cur.nexts) {
				// 更新他的邻居的入度
				inMap.put(node, inMap.get(node.value) - 1);
				if (inMap.get(node) == 0) {
					// 更新后为0 入队列
					queuq.add(node);
				}
			}
		}
		return result;

	}

127・拓扑排序 (opens new window)

DFS 解法 1

统计每个节点后面共有多少连通的节点，包括邻接节点的数量，如果两节点作比较数量较大的应该拓扑序在前，数量较小的拓扑序在后。

	public static class DirectedGraphNode {
		public int label;
		public ArrayList<DirectedGraphNode> neighbors;

		public DirectedGraphNode(int x) {
			label = x;
			neighbors = new ArrayList<DirectedGraphNode>();
		}
	}

	public static class info {
		DirectedGraphNode node; //当前节点
		long nodes; //当前节点连同节点的数量

		public info(DirectedGraphNode node, long nodes) {
			super();
			this.node = node;
			this.nodes = nodes;
		}

	}

	public ArrayList<DirectedGraphNode> topSort(ArrayList<DirectedGraphNode> graph) {
		// key为节点 value为节点和节点数包装类
		HashMap<DirectedGraphNode, info> map = new HashMap<>();
		//遍历拓扑结构 得到info信息存储到map中
		for (DirectedGraphNode directedGraphNode : graph) {
			f(directedGraphNode, map);
		}
		//存储所有info信息放入集合
		ArrayList<info> recordArr = new ArrayList<>();
		for (info info : map.values()) {
			recordArr.add(info);
		}
		//进行排序 节点数量多放前 少放后
		Collections.sort(recordArr, new Comparator<info>() {

			@Override
			public int compare(info o1, info o2) {
				// 无法强制成int 强转后出错
				return o1.nodes == o2.nodes ? 0 : (o1.nodes > o2.nodes ? -1 : 1);
			}
		});
		//结果集合
		ArrayList<DirectedGraphNode> res = new ArrayList<>();
		for (info info2 : recordArr) {
			res.add(info2.node);
		}
		return res;

	}

	// 返回当前节点 所有连同节点的个数的map
	private info f(DirectedGraphNode directedGraphNode, HashMap<DirectedGraphNode, info> map) {
		if (map.containsKey(directedGraphNode)) {
			// 如果之前有数据 则直接取出
			return map.get(directedGraphNode);
		}
		// 之前没算过
		long nodes = 0;
		for (DirectedGraphNode next : directedGraphNode.neighbors) {
			nodes += f(next, map).nodes; // 递归
		}
		info ans = new info(directedGraphNode, nodes + 1);
		// 更新存储数据
		map.put(directedGraphNode, ans);
		return ans;

	}

DFS 解法 2

我们求出每个节点的最大深度，根据每个节点的深度进行排序，深度大的放前，深度小的放后。

	public static class DirectedGraphNode {
		public int label;
		public ArrayList<DirectedGraphNode> neighbors;

		public DirectedGraphNode(int x) {
			label = x;
			neighbors = new ArrayList<DirectedGraphNode>();
		}
	}

	public static class info {
		DirectedGraphNode node; // 当前节点
		int deep; // 当前节点的最大深度

		public info(DirectedGraphNode node, int deep) {
			super();
			this.node = node;
			this.deep = deep;
		}

	}

	public ArrayList<DirectedGraphNode> topSort(ArrayList<DirectedGraphNode> graph) {
		HashMap<DirectedGraphNode, info> map = new HashMap<>();
		for (DirectedGraphNode node : graph) {
			f(node, map); // 求每个节点的深度
		}
		ArrayList<info> recordArr = new ArrayList<>();
		for (info info : map.values()) {
			recordArr.add(info);
		}
		Collections.sort(recordArr, (o1, o2) -> (o2.deep - o1.deep));
		ArrayList<DirectedGraphNode> ans = new ArrayList<>();
		for (info info : recordArr) {
			ans.add(info.node);
		}
		return ans;
		
	}

	private info f(DirectedGraphNode node, HashMap<DirectedGraphNode, info> map) {
		if (map.containsKey(node)) {
			// 有记录直接返回
			return map.get(node);
		}
		int follow = 0;
		for (DirectedGraphNode next : node.neighbors) {
			follow = Math.max(follow, f(next, map).deep);
		}
		info ans = new info(node, follow + 1); // 深度加上自身
		map.put(node, ans);
		return ans;

	}

最小生成树

Kruskal

克鲁斯卡尔算法查找最小生成树的方法是：将连通网中所有的边按照权值大小做升序排序，从权值最小的边开始选择，只要此边不和已选择的边一起构成环路，就可以选择它组成最小生成树。对于 N 个顶点的连通网，挑选出 N-1 条符合条件的边，这些边组成的生成树就是最小生成树。

举个例子，图 1 是一个连通网，克鲁斯卡尔算法查找图 1 对应的最小生成树，需要经历以下几个步骤：

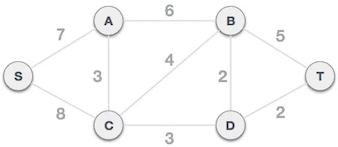
1. 将连通网中的所有边按照权值大小做升序排序：

2. 从 B-D 边开始挑选，由于尚未选择任何边组成最小生成树，且 B-D 自身不会构成环路，所以 B-D 边可以组成最小生成树。

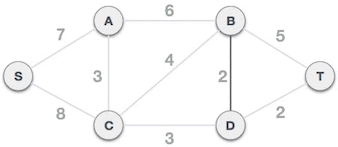
3. D-T 边不会和已选 B-D 边构成环路，可以组成最小生成树：

   

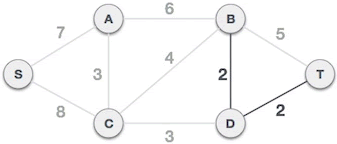
4. C-B 边会和已选 C-D、B-D 边构成环路，因此不能组成最小生成树：

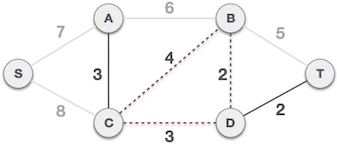
5. 直到生成所有点 或者 权值大小集合遍历完则生成完成最小生成树

   

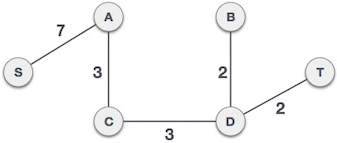
• 总是从取权值最小的边开始考虑
• 当前边要么进入最小生成树的集合，要么丢弃
• 如果当前的边进入最小生成树的集合中不会形成环，就要当前边
• 如果当前的边进入最小生成树的集合中会形成环，就不要当前边
• 考察完所有边之后，最小生成树的集合也得到了

模板写法：

1. 并查集
2. 权值集合最小堆 / 进行排序
3. 查询当前权值的两节点是否连同如无连同则连同，并合并并查集

	public class Node {
		public int value;
		public int in; // 入度
		public int out; // 出度
		public ArrayList<Node> nexts; // 当前节点出发有哪些邻居节点
		public ArrayList<Edge> edges; // 从当前节点出发有哪些边

		public Node(int value) {
			this.value = value;
			in = 0;
			out = 0;
			nexts = new ArrayList<>();
			edges = new ArrayList<>();
		}
	}

	public class Edge {
		public int weight; // 权重
		public Node from; // 父节点
		public Node to; // 子节点

		public Edge(int weight, Node from, Node to) {
			this.weight = weight;
			this.from = from;
			this.to = to;
		}

	}
	
	public class Graph {
		public HashMap<Integer, Node> nodes;// key存储为value value存储为Node节点
		public HashSet<Edge> edges;

		public Graph() {
			nodes = new HashMap<>();
			edges = new HashSet<>();
		}
	}

	
	public static class UnionFind {
		// 每个节点当前所在集合的父节点
		HashMap<Node, Node> fatherMap;
		// 每个节点当前所在集合的size
		HashMap<Node, Integer> sizeMap;

		public UnionFind() {
			fatherMap = new HashMap<>();
			sizeMap = new HashMap<>();
		}

		// 初始化
		public void makeSet(Collection<Node> nodes) {
			fatherMap.clear();
			sizeMap.clear();
			for (Node node : nodes) {
				fatherMap.put(node, node);
				sizeMap.put(node, 1);
			}
		}

		// 查找父节点+路径压缩
		public Node find(Node node) {
			Stack<Node> path = new Stack<>();
			while (node != fatherMap.get(node)) {
				path.add(node);
				node = fatherMap.get(node);
			}

			while (!path.isEmpty()) {
				fatherMap.put(path.pop(), node);
			}
			return node;
		}

		public boolean isSameSet(Node a, Node b) {
			return find(a) == find(b);
		}

		public void union(Node a, Node b) {
			if (a == null || b == null) {
				return;
			}
			Node f1 = find(a);
			Node f2 = find(b);
			if (f1 != f2) {
				Integer f1Size = sizeMap.get(f1);
				Integer f2Size = sizeMap.get(f2);
				if (f1Size >= f2Size) {
					fatherMap.put(b, a);//更新父节点
					sizeMap.put(a, f1Size+f2Size); //合并大小
					fatherMap.remove(b); //从并查集集合中移除合并后的节点
				} else {
					fatherMap.put(b, a);
					sizeMap.put(b, f2Size+f1Size);
					fatherMap.remove(a);
				}
			}
		}

	}
	
	
	public static Set<Edge> kruskalMST(Graph graph){
		UnionFind unionFind = new UnionFind();
		unionFind.makeSet(graph.nodes.values()); //初始化并查集
		//最小堆 以权值排序
		PriorityQueue<Edge> priorityQueue = new PriorityQueue<>((o1,o2) -> (o1.weight - o2.weight));
		
		for (Edge edge : graph.edges) {
			priorityQueue.add(edge); //加入堆中
		}
		Set<Edge> result = new HashSet<>();
		while(!priorityQueue.isEmpty()) {
			Edge edge =  priorityQueue.poll();
			//查看 from 和 to 两节点是否在一个集合中 如之前合并过则不进行操作 从堆中弹出
			if(!unionFind.isSameSet(edge.from, edge.to)) {
				result.add(edge); //添加到最小生成树结果集合中
				unionFind.union(edge.from, edge.to); //合并两节点
			}
		}
		return result;
		
		
		
	}

Prim

1. 寻找图中任意点，以它为起点，它的所有边 V 加入集合 (优先队列) q1 , 设置一个 boolean数组bool[] 标记该位置已经确定。
2. 从集合 q1 找到距离最小的那个边 v1 并判断边另一点 p 是否被标记 (访问)，如果 p 被标记说明已经确定那么跳过，如果未被标 (访问) 记那么标记该点 p , 并且与 p 相连的未知点 (未被标记) 构成的边加入集合 q1 ，边 v1 (可以进行计算距离之类，该边构成最小生成树) .
3. 重复 1，2 直到 q1 为空，构成最小生成树 ！

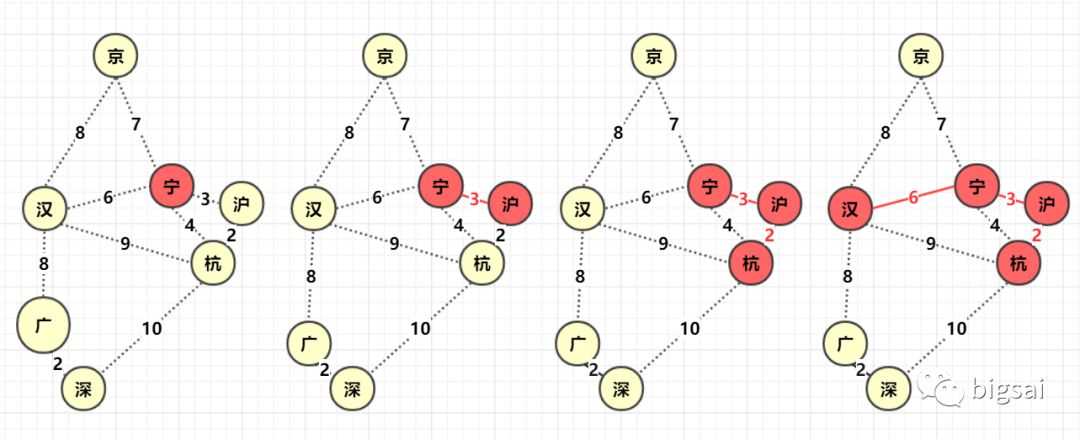
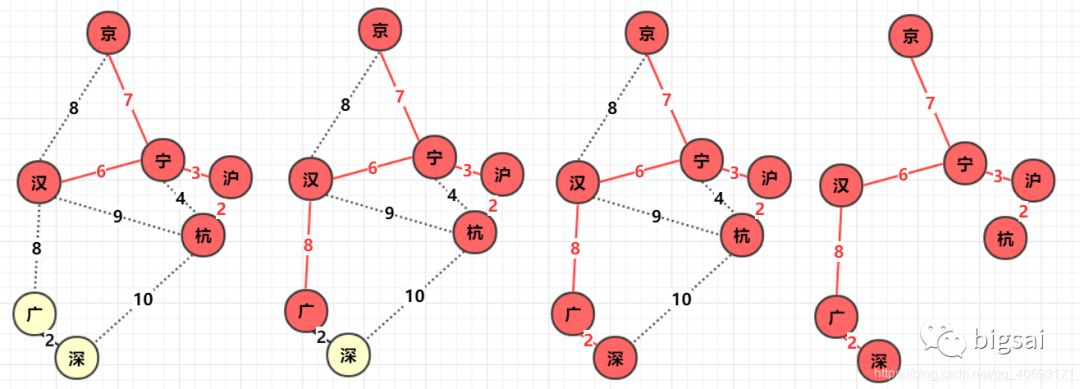
因为 prim 从开始到结束一直是一个整体在扩散，所以不需要考虑两棵树合并的问题，在这一点实现上稍微方便了一点。

当然，要注意的是最小生成树并不唯一，甚至同一种算法生成的最小生成树都可能有所不同，但是相同的是无论生成怎样的最小生成树：

• 能够保证所有节点连通 (能够满足要求和条件)
• 能够保证所有路径之和最小 (结果和目的相同)
• 最小生成树不唯一，可能多样的如下

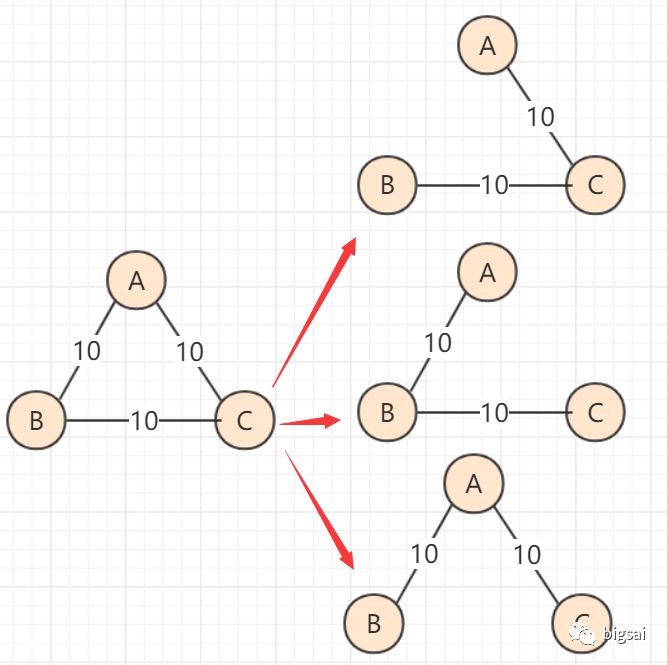
	public class Node {
		public int value;
		public int in; // 入度
		public int out; // 出度
		public ArrayList<Node> nexts; // 当前节点出发有哪些邻居节点
		public ArrayList<Edge> edges; // 从当前节点出发有哪些边

		public Node(int value) {
			this.value = value;
			in = 0;
			out = 0;
			nexts = new ArrayList<>();
			edges = new ArrayList<>();
		}
	}

	public class Edge {
		public int weight; // 权重
		public Node from; // 父节点
		public Node to; // 子节点

		public Edge(int weight, Node from, Node to) {
			this.weight = weight;
			this.from = from;
			this.to = to;
		}

	}

	public class Graph {
		public HashMap<Integer, Node> nodes;// key存储为value value存储为Node节点
		public HashSet<Edge> edges;

		public Graph() {
			nodes = new HashMap<>();
			edges = new HashSet<>();
		}
	}

	public static Set<Edge> primMST(Graph graph) {
		// 解锁的边 放人小根堆中
		PriorityQueue<Edge> queue = new PriorityQueue<>((o1, o2) -> (o1.weight - o2.weight));

		// 有哪些点被解锁过 已经被连同过的
		HashSet<Node> nodeSet = new HashSet<>();

		// 最小生成树节点顺序集合
		HashSet<Edge> reslut = new HashSet<>();

		// 从任意点开始
		for (Node node : graph.nodes.values()) {
			// 如果当前点未被使用过
			if (!nodeSet.contains(node)) {
				nodeSet.add(node); // 添加到使用过的集合
				// 遍历它的邻接点 加入到小根堆中
				for (Edge edge : node.edges) {
					queue.add(edge);
				}
				while (!queue.isEmpty()) {
					Edge edge = queue.poll(); // 弹出解锁边中 最小
					Node toNode = edge.to; // 最小权值的 to节点
					if (!nodeSet.contains(toNode)) { // 该节点没有被解锁过 即使用当前最小边的节点 不会形成环
						nodeSet.add(toNode); // 加到解锁节点的集合
						reslut.add(edge); // 结果集合
						for (Edge nextEdge : toNode.edges) {
							queue.add(nextEdge); // 将当前的新解锁节点的邻接节点放入小根堆中
						}
					}
				}

			}
			break;

		}

		return reslut;

	}

单元最短路径算法 Dijkstra

狄克斯特拉算法是从一个顶点到其余各顶点的最短路径算法，解决的是有权图中最短路径问题。迪杰斯特拉算法主要特点是从起始点开始，采用贪心算法的策略，每次遍历到始点距离最近且未访问过的顶点的邻接节点，直到扩展到终点为止。

狄克斯特拉算法默认为无负值权值边，如果多个节点成环，并且多个权值的和为负值的会出现无法得出最短路径。

假设 v1 为源点，找从 v1 到其它节点的最短路径

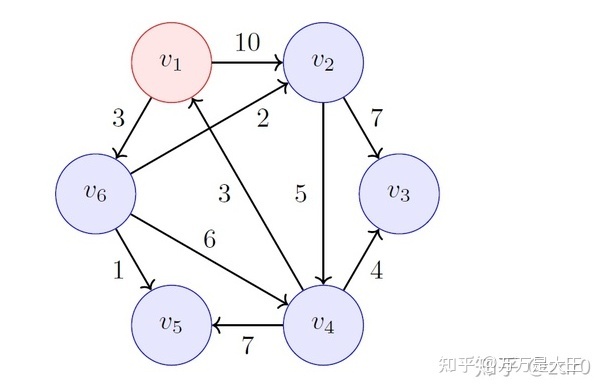
• 集合 S 用来存储已经找到的最短路径
• v1 到自己显然最短，故为初始最短路径

第一轮：从 v1 出发，计算 v1 到其它节点的距离（无法连接则用 “无穷” 符号）

• 全表找最小值，发现 v1 到 v6 最短为 3
• S 中添加一条最短路径：v1——v6
• v6 列标红不再考虑

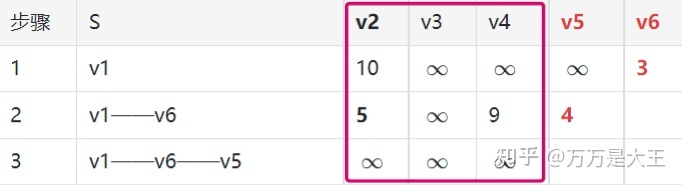
第二轮：从 v1——v6 出发，计算 v1 通过 v6 到其它节点的距离

已知 v1 到 v6 为 3；v6 可以到 v2,v4,v5；因此，v1 通过 v6 到其它节点的距离为 3+n，n 为 6 到各节点的距离

• 在全表中找最小值（v6 列已经删除），此时 4 为最小值，对应路径 v1——v6——v5
• 添加最短路径 v1——v6——v5
• v5 列不再考虑

第三轮：从 v1——v6——v5 出发，计算 v1 通过 v6 及 v5 到其它节点的距离

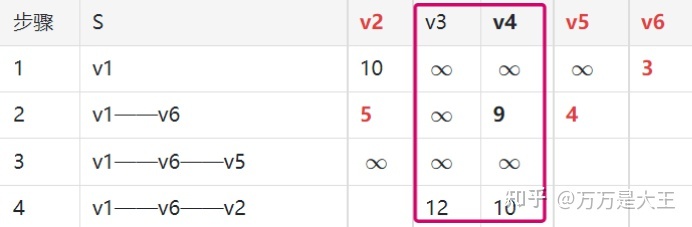
第四轮：从 v1——v6——v2 出发，计算 v1 通过 v6 及 v2 到其它节点的距离

第五轮：从 v1——v6——v4 出发，计算 v1 通过 v6 及 v4 到其它节点的距离

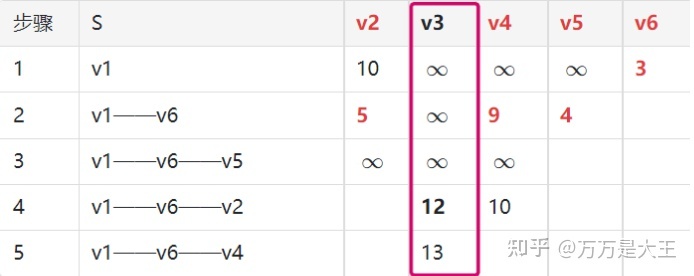
	public class Node {
		public int value;
		public int in; // 入度
		public int out; // 出度
		public ArrayList<Node> nexts; // 当前节点出发有哪些邻居节点
		public ArrayList<Edge> edges; // 从当前节点出发有哪些边

		public Node(int value) {
			this.value = value;
			in = 0;
			out = 0;
			nexts = new ArrayList<>();
			edges = new ArrayList<>();
		}
	}

	public class Edge {
		public int weight; // 权重
		public Node from; // 父节点
		public Node to; // 子节点

		public Edge(int weight, Node from, Node to) {
			this.weight = weight;
			this.from = from;
			this.to = to;
		}

	}

	public class Graph {
		public HashMap<Integer, Node> nodes;// key存储为value value存储为Node节点
		public HashSet<Edge> edges;

		public Graph() {
			nodes = new HashMap<>();
			edges = new HashSet<>();
		}
	}



	public static HashMap<Node, Integer> dijkstra1(Node node) {
		// key为节点 value为从头节点出单源最短路径值
		HashMap<Node, Integer> map = new HashMap<>();
		map.put(node, 0); // 自身到自身为0

		// 存储已经是最短路径的节点
		HashSet<Node> selectNode = new HashSet<>();
		Node minNode = getMinDistanceAndUnselectedNode(map, selectNode); // 获取没有被标记过 并且是当前单源最短路径的最小值 目前为node自身 为权值0
		while (minNode != null) {
			// 获取原始点 到 minNode 的最小权值距离
			Integer distance = map.get(minNode);
			// 遍历当前minNode所有边
			for (Edge edge : minNode.edges) {
				Node toNode = edge.to; // 边指向的节点
				if (!map.containsKey(toNode)) {
					// 说明当前指向的节点没有来过 更新为当前minNode的权值 + 当前边权值
					map.put(toNode, distance + edge.weight);

				} else {
					// 之前有记录 查看是否能更新为最小值
					map.put(toNode, Math.min(map.get(toNode), distance + edge.weight));
				}

			}
			selectNode.add(minNode); // 查找到去往下一个节点的最短路径 将当前的出发节点 打上标记 存储到已经是最短路径的节点集合
			minNode = getMinDistanceAndUnselectedNode(map, selectNode); // 获取没有被标记过 并且是当前单源最短路径的最小值的节点
		}
		return map;

	}

	public static Node getMinDistanceAndUnselectedNode(HashMap<Node, Integer> map, HashSet<Node> touchedNodes) {
		Node minNode = null;
		int minDistance = Integer.MAX_VALUE;
		// 遍历单源最短路径节点和值 散列集合
		for (Entry<Node, Integer> entry : map.entrySet()) {
			Node node = entry.getKey();
			Integer distance = entry.getValue();
			// 如果当前节点没有被标记为过已经是最短路径 并且当前权值是最小
			if (!touchedNodes.contains(node) && distance < minDistance) {
				minNode = node;
				minDistance = distance;
			}
		}
		return minNode;
	}

加强堆优化

	public class Node {
		public int value;
		public int in; // 入度
		public int out; // 出度
		public ArrayList<Node> nexts; // 当前节点出发有哪些邻居节点
		public ArrayList<Edge> edges; // 从当前节点出发有哪些边

		public Node(int value) {
			this.value = value;
			in = 0;
			out = 0;
			nexts = new ArrayList<>();
			edges = new ArrayList<>();
		}
	}

	public class Edge {
		public int weight; // 权重
		public Node from; // 父节点
		public Node to; // 子节点

		public Edge(int weight, Node from, Node to) {
			this.weight = weight;
			this.from = from;
			this.to = to;
		}

	}

	public class Graph {
		public HashMap<Integer, Node> nodes;// key存储为value value存储为Node节点
		public HashSet<Edge> edges;

		public Graph() {
			nodes = new HashMap<>();
			edges = new HashSet<>();
		}
	}

	public static class NodeRecord {
		Node node; // 节点
		int distance; // 开始源节点到当前节点最短路径的取值和

		public NodeRecord(Node node, int distance) {
			this.node = node;
			this.distance = distance;
		}
	}

	public static class NodeHeap {
		// 堆
		Node[] nodes;
		HashMap<Node, Integer> heapIndexMap; // 当前节点在小根堆数组的位置
		HashMap<Node, Integer> distanceMap; // 开始源节点到当前节点最短路径的取值和
		int size;

		public NodeHeap(int size) {
			this.size = size;
			nodes = new Node[size]; // 堆数组
			heapIndexMap = new HashMap<>();
			distanceMap = new HashMap<>();
		}

		public boolean isEmpty() {
			return size == 0;
		}

		// 判断当前节点是否在堆中 从索引表中查找
		public boolean isEnterd(Node node) {
			return heapIndexMap.containsKey(node);
		}

		// 判断当前节点是否被标记过为最短路径了 即之前成为过堆顶并被弹出过 如被弹过索引表中记录值应为-1
		public boolean inHeap(Node node) {
			// 在堆中 并且没有被标记为最短路径
			return isEnterd(node) && heapIndexMap.get(node) != -1;
		}

		// 加入堆中
		public void addOrUpdateOrigonre(Node node, int dijkstra) {
			// 更新节点 即存在与堆中 并且没有为标记为最短路径
			if (inHeap(node)) {
				// 更新为更小的权值点
				distanceMap.put(node, Math.min(distanceMap.get(node), dijkstra));

			}
		}

		// 往上移动
		public void insertHeapify(int index) {
			// 当前节点的权值 与 它的根节点比较大小 是否能上浮节点
			while (distanceMap.get(nodes[index]) < distanceMap.get(nodes[(index - 1) / 2])) {
				swap(index, (index - 1) / 2);
				index = (index - 1) / 2;
			}
		}

		// 下沉
		public void heapify(int index, int size) {
			int left = index * 2 + 1;
			while (left < size) {
				// 查找当前节点左右孩子的最小节点 判断是否能下沉
				int small = left + 1 < size && distanceMap.get(nodes[left + 1]) < distanceMap.get(nodes[left])
						? left + 1
						: left;
				// 左右孩子的最小节点 小于 当前下标
				small = distanceMap.get(nodes[small]) < distanceMap.get(index) ? small : index;
				if (small == index) {
					break; // 当前自身已经是最小的 无法下沉
				}
				swap(index, small);
				index = small;
				left = index * 2 + 1;
			}
		}

		// 弹出堆顶 最小值
		public NodeRecord pop() {
			// 封装节点 堆顶节点 最小路径和
			NodeRecord nodeRecord = new NodeRecord(nodes[0], distanceMap.get(nodes[0]));
			swap(0, size - 1); // 将堆顶交换到堆数组尾部
			heapIndexMap.put(nodes[size - 1], -1); // 将节点的索引表更新为-1
			distanceMap.remove(nodes[size - 1]); // 不再保存 当前节点的最短路径和
			nodes[size - 1] = null; // 释放节点
			heapify(0, --size); // 下沉交换的元素 即当前堆顶
			return nodeRecord;
		}

		// 交换元素
		private void swap(int index1, int index2) {
			heapIndexMap.put(nodes[index1], index2); // 更新索引表
			heapIndexMap.put(nodes[index2], index1);
			Node temp = nodes[index1];
			nodes[index1] = nodes[index2];
			nodes[index2] = temp;

		}

	}

	/**
	 * 加强堆实现的迪杰斯克拉算法
	 * 
	 * @param head 开始源节点
	 * @param size 一共有多少节点
	 * @return 返回为散列集合 key为节点 value为从开始源节点到当前节点最短路径的取值和
	 */
	public static HashMap<Node, Integer> dijkstra(Node head, int size) {
		NodeHeap nodeHeap = new NodeHeap(size);
		nodeHeap.addOrUpdateOrigonre(head, 0); // 源节点入加强堆 并且最短路径权值为0 自身到自身为0
		HashMap<Node, Integer> result = new HashMap<>(); // key为节点 value为从源节点到自身节点的最小路径权值和
		while (!nodeHeap.isEmpty()) {
			NodeRecord record = nodeHeap.pop(); // 弹出堆顶
			Node cur = record.node; // 当前节点
			int distance = record.distance; // 当前节点的最小路径权值和
			// 遍历当前节点所有邻接节点
			for (Edge edge : cur.edges) {
				// edge.to去往的节点 edge.weight为去往路径边的权值 要加上当前节点的最小路径和
				nodeHeap.addOrUpdateOrigonre(edge.to, edge.weight + distance);
			}
			result.put(cur, distance);

		}
		return result;

	}