单调栈

一种特别设计的栈结构，为了解决如下的问题：

给定一个可能含有重复值的数组 arr，i 位置的数一定存在如下两个信息

1. arr [i] 的左侧离 i 最近并且小于 (或者大于) arr [i] 的数在哪？

2. arr [i] 的右侧离 i 最近并且小于 (或者大于) arr [i] 的数在哪？

如果想得到 arr 中所有位置的两个信息，怎么能让得到信息的过程尽量快。

单调栈：生成每一个位置的左边跟右边离它最近的比它小的信息，并且可以做到整体 O (N) 拿下

	public static int[][] getNearLessNoRepeat(int[] arr) {
		int[][] res = new int[arr.length][2];
		// 只存位置！
		Stack<Integer> stack = new Stack<>();
		for (int i = 0; i < arr.length; i++) { // 当遍历到i位置的数，arr[i]
            //栈不为空 当前栈顶的数大于当前数 需要把栈顶弹出后才能入栈
			while (!stack.isEmpty() && arr[stack.peek()] > arr[i]) {
                //弹出栈顶
				int j = stack.pop();
                //当前数的左侧最近并且小arr[j](即之前栈顶)的位置  弹出后栈为空设置为-1 否则为当前栈顶
                //因为栈是从小到大 栈顶必大于 arr[i]  
				int leftLessIndex = stack.isEmpty() ? -1 : stack.peek();
                //设置被弹出的数 的左侧最近并且小于它的位置
				res[j][0] = leftLessIndex;
                //设置被弹出的数 的右侧最近并且小于它的位置
				res[j][1] = i;
			}
            //栈为空/当前arr[i]大于栈顶的数
			stack.push(i);
		}
        //遍历完数组后 栈不为空则说明 它们右侧没有大于它自身的数
		while (!stack.isEmpty()) {
            //弹出栈顶
			int j = stack.pop();
            //判断栈是否为空 不为空说明有它左侧最近并且小于它的位置
			int leftLessIndex = stack.isEmpty() ? -1 : stack.peek();
			res[j][0] = leftLessIndex;
            //右边恒定没有
			res[j][1] = -1;
		}
		return res;
	}

	//当出现相同元素情况 使用链表挂载
	public static int[][] getNearLess(int[] arr) {
		int[][] res = new int[arr.length][2];
		Stack<List<Integer>> stack = new Stack<>();
		for (int i = 0; i < arr.length; i++) { // i -> arr[i] 进栈
			while (!stack.isEmpty() && arr[stack.peek().get(0)] > arr[i]) {
				List<Integer> popIs = stack.pop();
				int leftLessIndex = stack.isEmpty() ? -1 : stack.peek().get(stack.peek().size() - 1);
				for (Integer popi : popIs) {
					res[popi][0] = leftLessIndex;
					res[popi][1] = i;
				}
			}
			if (!stack.isEmpty() && arr[stack.peek().get(0)] == arr[i]) {
				stack.peek().add(Integer.valueOf(i));
			} else {
				ArrayList<Integer> list = new ArrayList<>();
				list.add(i);
				stack.push(list);
			}
		}
		while (!stack.isEmpty()) {
			List<Integer> popIs = stack.pop();
            //注意这里是取链表中最后一个元素(即最大/最近位置)
			int leftLessIndex = stack.isEmpty() ? -1 : stack.peek().get(stack.peek().size() - 1);
			for (Integer popi : popIs) {
				res[popi][0] = leftLessIndex;
				res[popi][1] = -1;
			}
		}
		return res;
	}

42. 接雨水 (opens new window)

双指针

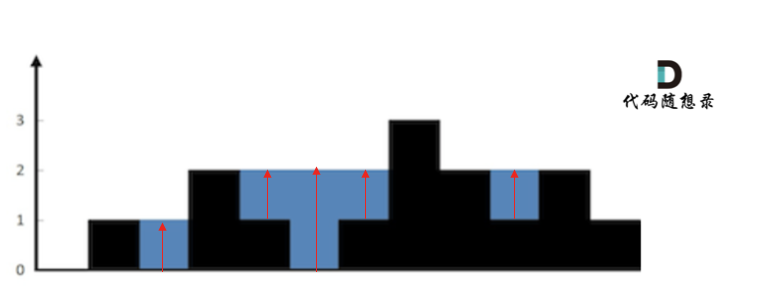
如果按照列来计算的话，宽度一定是 1 了，我们再把每一列的雨水的高度求出来就可以了

每一列雨水的高度，取决于，该列左侧最高的柱子和右侧最高的柱子中最矮的那个柱子的高度。

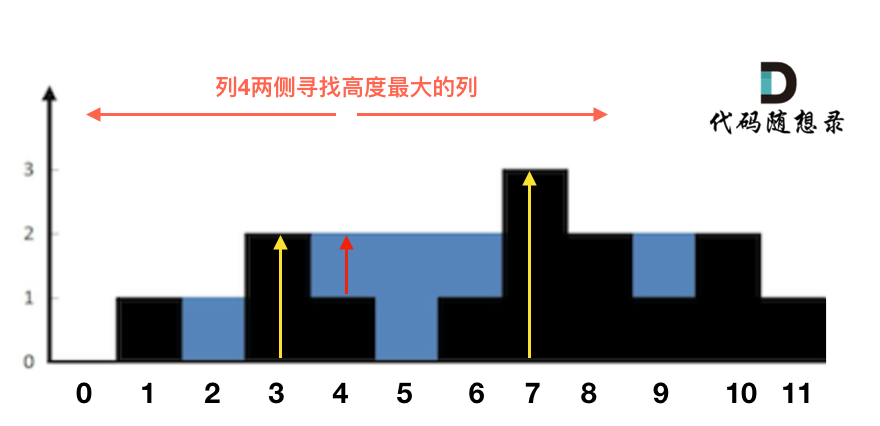
如果想求第 4 列的雨水高度需要以下三步

1. 求出该列左侧最高的柱子是列 3，高度为 2（我们用 lHeight 表示）
2. 求出该列右侧最高的柱子是列 7，高度为 3（我们用 rHeight 表示）
3. 该列的高度为 1

则列 4 的雨水高度为列 3 和列 7 的高度最小值减列 4 高度，即$min(\text{lHeight},\text{rHeight})-height=min(2,3)-1=1$

列 4 的雨水高度求出来了，宽度为 1；只要从头遍历一遍所有的列，然后求出每一列雨水的体积，相加之后就是总雨水的体积了。

public int trap(int[] height) {
    int sum = 0;
    for (int i = 0; i < height.length; i++) {
        // 第一个柱子和最后一个柱子不接雨水，因为边界无另外一边无法容纳雨水
        if (i==0 || i== height.length - 1) continue;

        int rHeight = height[i]; // 记录右边柱子的最高高度
        int lHeight = height[i]; // 记录左边柱子的最高高度
        //找出当前列左侧最高的柱子
        for (int r = i+1; r < height.length; r++) {
            if (height[r] > rHeight) rHeight = height[r];
        }
        //找出当前列右侧最高的柱子
        for (int l = i-1; l >= 0; l--) {
            if(height[l] > lHeight) lHeight = height[l];
        }
        //求出两侧最矮的柱子减去当前列高度则为当前列的雨水容量
        int h = Math.min(lHeight, rHeight) - height[i];
        if (h > 0) sum += h;
    }
    return sum;

}

优化

在上面的方法中，我们计算每一列的左右列最高值时总是重复遍历一遍，可以开辟一个数组用于存放每一个位置的左边最高高度记录在一个数组上（maxLeft），右边最高高度记录在一个数组上（maxRight），这样就避免了重复计算。

public int trap(int[] height) {
    if (height.length <= 2) return 0;
    int n = height.length;
    int[] maxLeft = new int[n];
    int[] maxRight = new int[n];

    // 记录每个柱子左边柱子最大高度
    maxLeft[0] = height[0];
    //注意边界不容纳雨水
    for (int i = 1; i < n; i++) {
        maxLeft[i] = Math.max(height[i], maxLeft[i - 1]);
    }
    // 记录每个柱子右边柱子最大高度
    maxRight[n - 1] = height[n - 1];
    //注意边界不容纳雨水
    for (int i = n - 2; i >= 0; i--) {
        maxRight[i] = Math.max(height[i], maxRight[i + 1]);
    }
    // 求和
    int sum = 0;
    for (int i = 0; i < n; i++) {
        int count = Math.min(maxLeft[i], maxRight[i]) - height[i];
        if (count > 0) sum += count;
    }
    return sum;
}

单调栈

    public int trap(int[] height) {
        if(height.length <= 2){
            return 0;
        }
        Stack<Integer> stack = new Stack<>();
        stack.push(0); // 将首个元素入栈

        int sum = 0;
        for(int index = 1;index < height.length; index++){
            // 查看栈顶
            int stackFist = stack.peek();
            // 判断当前将要入栈的元素 是否小于栈顶
            if(height[index] < height[stackFist]){
                stack.push(index); //小于则直接入栈
            } else if (height[index] == height[stackFist]){ // 判断当前将要入栈的元素 是否等于栈顶
                stack.pop(); //小于 则当前栈顶不可能成为将要入栈元素的左墙壁 将栈顶弹出
                stack.push(index); //入栈当前元素作为下一个元素的左墙壁
            } else { // 当前将要入栈元素 大于栈顶
                //说明当前栈顶 为获取雨水的值
                int rainRight = height[index]; // 雨水的右墙壁
                // 栈不为空 
                while( !stack.isEmpty() && (rainRight >= height[stackFist]) ){
                    int mid = stack.pop(); //当前栈顶 并且弹出
                    if(!stack.isEmpty()){ //再次查看栈是否为空
                        int left = stack.peek();  //查看栈顶 当前栈顶为左墙壁
                        //left为左墙壁  index为右墙壁  mid为雨水
                        int h = Math.min(height[left],height[index]) - height[mid]; //雨水高度
                        int w = index - left -1; //雨水的宽度
                        sum += h*w; // 当前雨水
                        stackFist = stack.peek(); //将之前的最先开始缓存的栈顶 更新为当前栈顶 用于查找雨水的宽度
                    }
                }
                stack.push(index); //当前元素入栈
            }
        }
        return sum;


    }