 串
串
# 串
# 定义基本操作
# 串的定义
串,即字符串(String)是由零个或多个字符组成的有限序列。一般记为
其中,S 是串名,单引号括起来的字符序列是串的值;
有的地方用双引号(如 Java、C), 有的地方用单引号(如 Python)
S="HelloWorld!";
1
T='iPhone 11 Pro Max?'
1
- 子串: 串中任意个连续的字符组成的子序列。 Eg:’iPhone’,’Pro M’ 是串 T 的子串
- 主串: 包含子串的串。 Eg:T 是子串’iPhone’的主串
- 字符在主串中的位置: 字符在串中的序号。 Eg:’1’在 T 中的位置是 8 (第一次出现)
- 子串在主串中的位置: 子串的第一个字符在主串中的位置 。 Eg:’11 Pro’在 T 中的位置为 8;注意:位序从 1 开始而不是从 0 开始
M=''; //M是空串
N=' '; //N是由三个空格字符组成的空格串,每个空格字符占1B
1
2
2
串是一种特殊的线性表,数据元素之间呈线性关系

串的数据对象限定为字符集(如中文字符、英文字符、数字字符、标点字符等)
串的基本操作,如增删改查等通常以子串为操作对象
# 串的基本操作
StrAssign(&T,chars):赋值操作。把串 T 赋值为 chars。StrCopy(&T,S):复制操作。由串 S 复制得到串 T。StrEmpty(S):判空操作。若 S 为空串,则返回 TRUE,否则返回 FALSE。StrLength(S):求串长。返回串 S 的元素个数。ClearString(&S):清空操作。将 S 清为空串。DestroyString(&S):销毁串。将串 S 销毁(回收存储空间)。Concat(&T,S1,S2):串联接。用 T 返回由 S1 和 S2 联接而成的新串SubString(&Sub,S,pos,len):求子串。用 Sub 返回串 S 的第 pos 个字符起长度为 len 的子串。Index(S,T):定位操作。若主串 S 中存在与串 T 值相同的子串,则返回它在主串 S 中第一次出现的位置;否则函数值为 0。StrCompare(S,T):比较操作。若 S>T,则返回值 > 0;若 S=T,则返回值 = 0;若 S<T,则返回值 < 0。- 从第一个字符开始往后依次对比,先出现更大字符的串就更大
- 长串的前缀与短串相同时,长串更大
- 只有两个串完全相同时,才相等
# 字符集编码
任何数据存到计算机中一定是二进制数。需要确定一个字符和二进制数的对应规则这就是 “编码”
“字符集”:英文字符 ——ASCII 字符集,中英文 ——Unicode 字符集等多种编码
注:采用不同的编码方式,每个字符所占空间不同,考研中只需默认每个字符占 1B 即可
# 串的存储结构
# 串的顺序存储
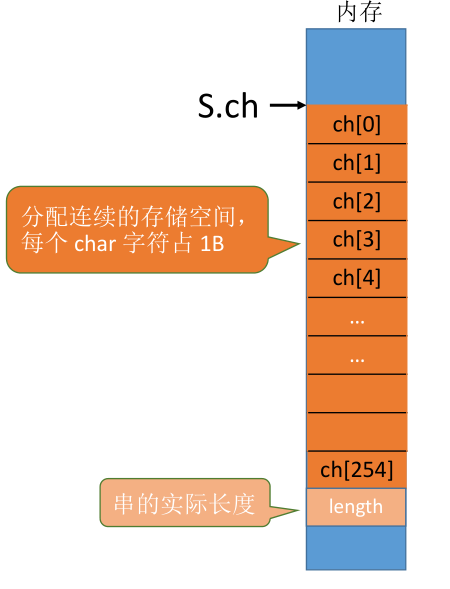
#define MAXLEN 255 //预定义最大串长为255
typedef struct {
char ch[MAXLEN]; //每个分量存储一个字符
int length; //串的实际长度
} SString;
typedef struct {
char *ch; //按串长分配存储区,ch指向串的基地址
int length; //串的长度
} HString;
void testString() {
HString S;
S.ch = (char *)malloc(MAXLEN * sizeof(char)); // 用完需要手动free
S.length = 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
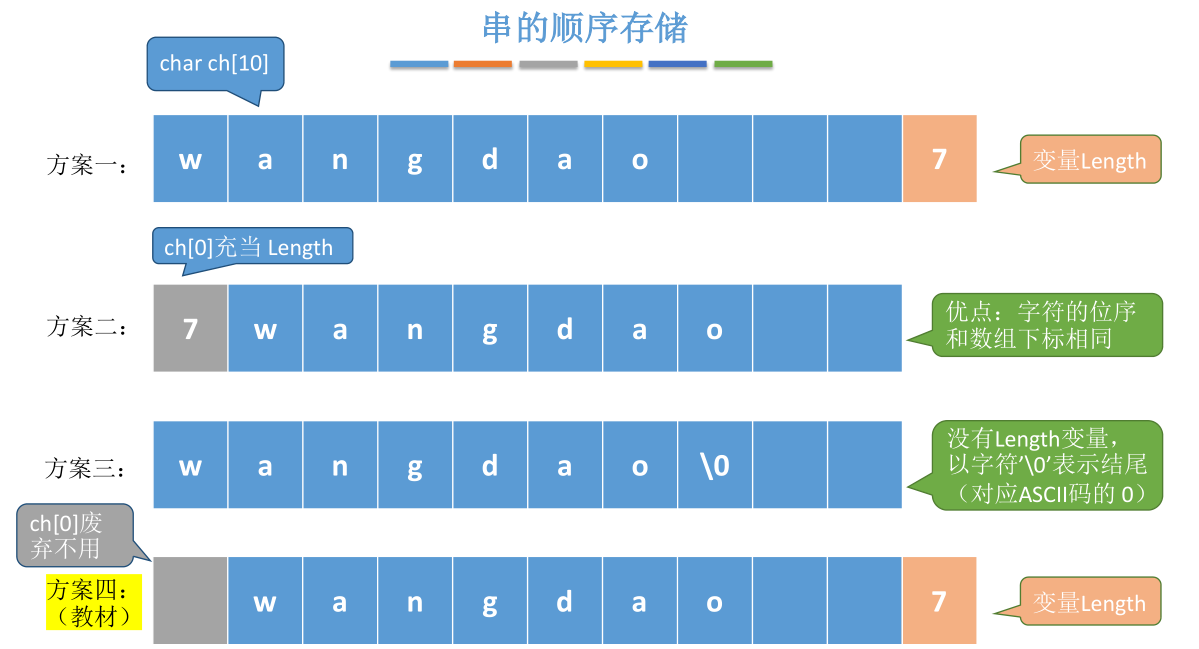
下面代码默认会从下标 1 开始访问,ch [0] 废弃不用。
# 串的链式存储
typedef struct StringNode {
char ch; //每个结点存储1个字符
struct StringNode * next;
} StringNode, *String;
1
2
3
4
2
3
4

#define N 4
typedef struct StringNode {
char ch[N]; //每个结点存储多个字符
struct StringNode * next;
} StringNode, *String;
1
2
3
4
5
2
3
4
5

# 基本操作的实现

SubString(&Sub,S,pos,len):求子串。用 Sub 返回串 S 的第 pos 个字符起长度为 len 的子串。
#define MAXLEN 255 //预定义最大串长为255
typedef struct {
char ch[MAXLEN]; //每个分量存储一个字符
int length; //串的实际长度
} SString;
//求子串
bool SubString(SString &Sub, SString S, int pos, int len) {
//子串范围越界
if (pos + len - 1 > S.length) {
return false;
}
for (int i = pos; i < pos + len; i++)
{
Sub.ch[i - pos + 1] = S.ch[i];
}
Sub.length = len;
return true;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
StrCompare(S,T):比较操作。若 S>T,则返回值 > 0;若 S=T,则返回值 = 0;若 S<T,则返回值 < 0。
//比较操作
int StrCompare(SString S, SString T) {
for (int i = 1; i <= S.length && i <= T.length; i++)
{
if (S.ch[i] != T.ch[i]) {
return S.ch[i] - T.ch[i];
}
}
// 扫描过的所有字符都相同,则长度长的串更大
return S.length - T.length;
}
1
2
3
4
5
6
7
8
9
10
11
2
3
4
5
6
7
8
9
10
11
Index(S,T):定位操作。若主串 S 中存在与串 T 值相同的子串,则返回它在主串 S 中第一次出现的位置;否则函数值为 0。
//定位操作
int Index(SString S, SString T) {
int i = 1, n = SS.length, m = SS.length;
SString sub; //存储子串
while (i < n - m + 1) {
SubString(sub, S, i, m);
if (StrCompare(sub, T) != 0) {
++i;
} else {
return i; //返回子串在主串中的位置
}
}
return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
2
3
4
5
6
7
8
9
10
11
12
13
14
# 总结
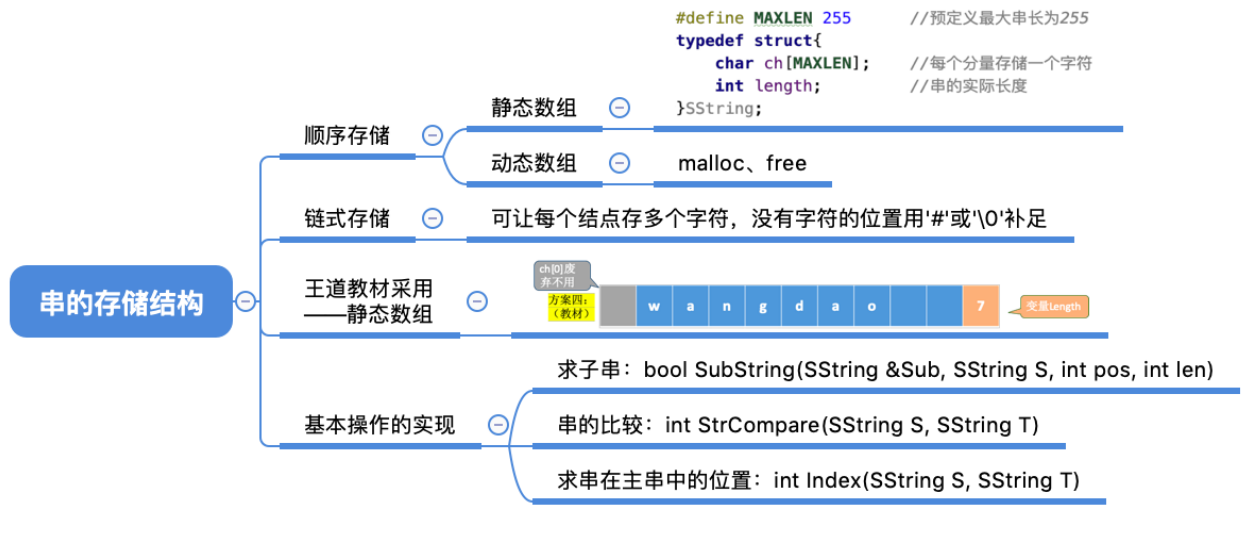
# 字符串模式匹配
字符串模式匹配:在主串中找到与模式串相同的子串,并返回其所在位置。

- 子串 —— 主串的⼀部分,⼀定存在
- 模式串 —— 不⼀定能在主串中找到
# 朴素模式匹配算法
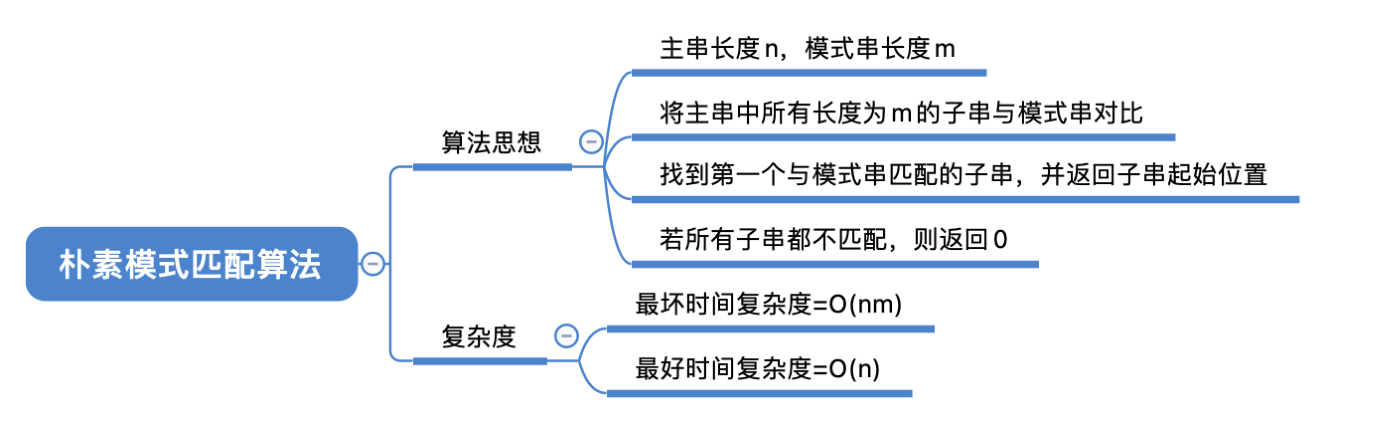
主串长度为 n,模式串长度为 m
朴素模式匹配算法:将主串中所有长度为 m 的子串依次与模式串对比,直到找到⼀个完全匹配的子串,或所有的子串都不匹配为止。
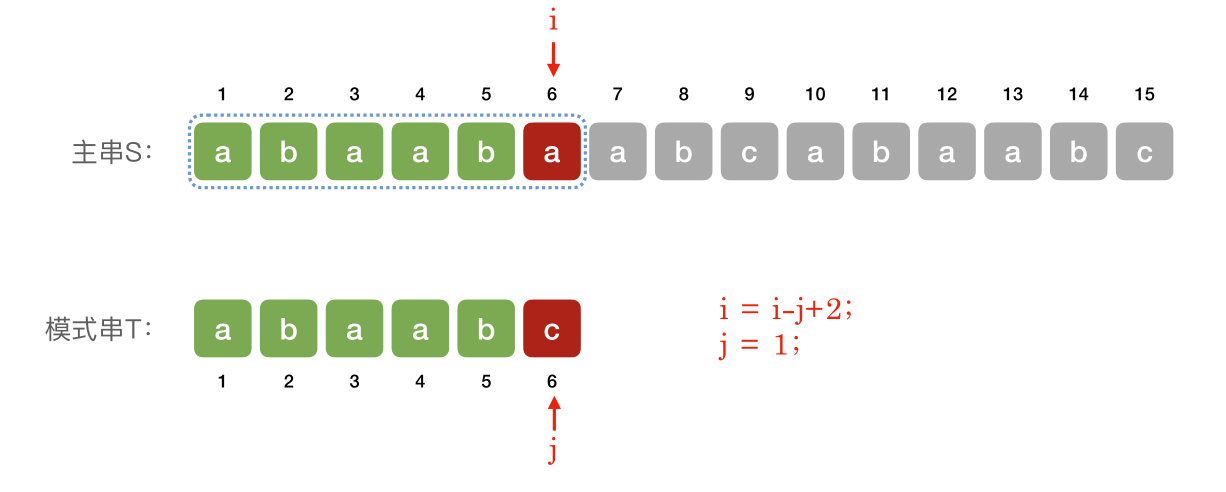
若当前⼦串匹配失败,则主串指针 i 指向下⼀个⼦串的第⼀个位置,模式串指针 j 回到模式串的第⼀个位置
//朴素模式匹配算法
int Index(SString S, SString T) {
int i = 1, i = 1;
while (i < S.length && j < T.length) {
if (S.ch[i] == T.ch[j]) {
++i; ++j; //继续比较后继字符
} else {
i = i - j + 2;
j = 1; //指针后退重新开始匹配
}
}
if (j > T.length) {
return i - T.length;
} else {
return 0;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
最坏时间复杂度 =
# 总结
# KMP 算法
由 D.E.Knuth,J.H.Morris 和 V.R.Pratt 提出,因此称为 KMP 算法
# 朴素模式匹配算法优化思路
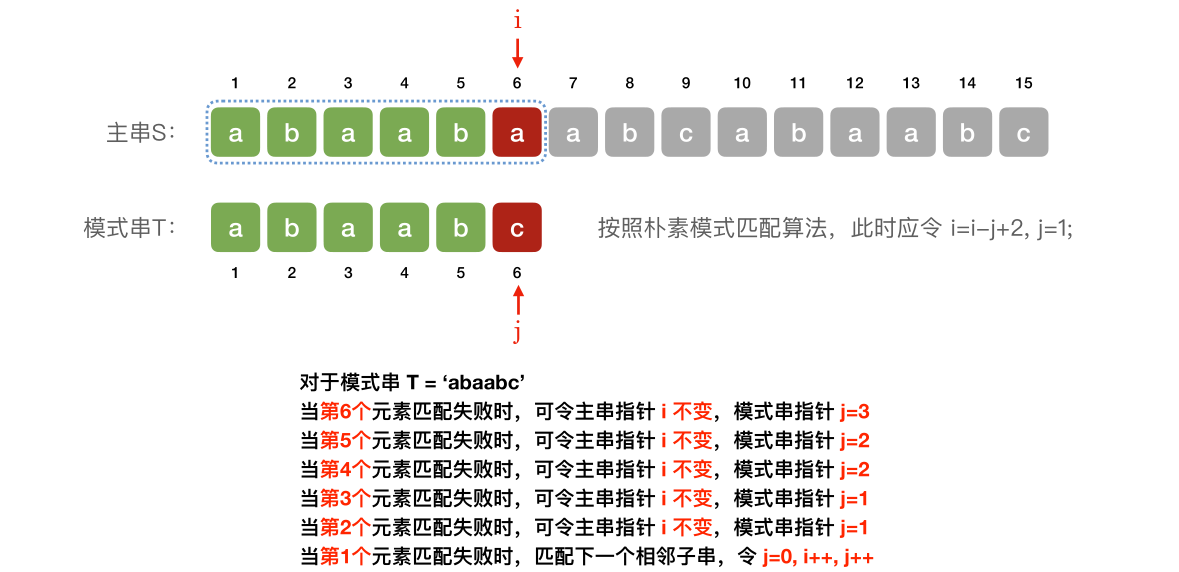
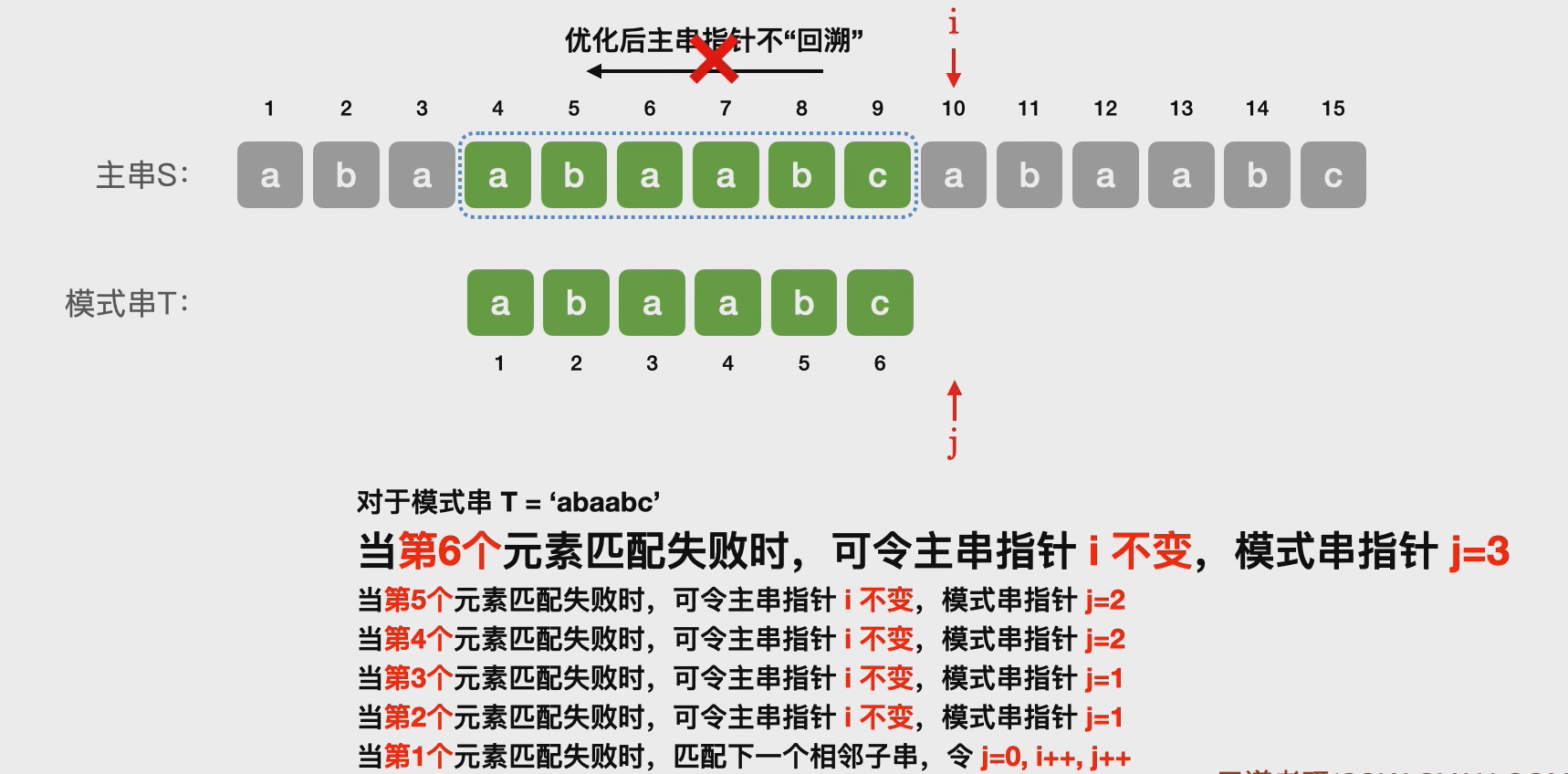
怎么用代码实现这个处理逻辑?
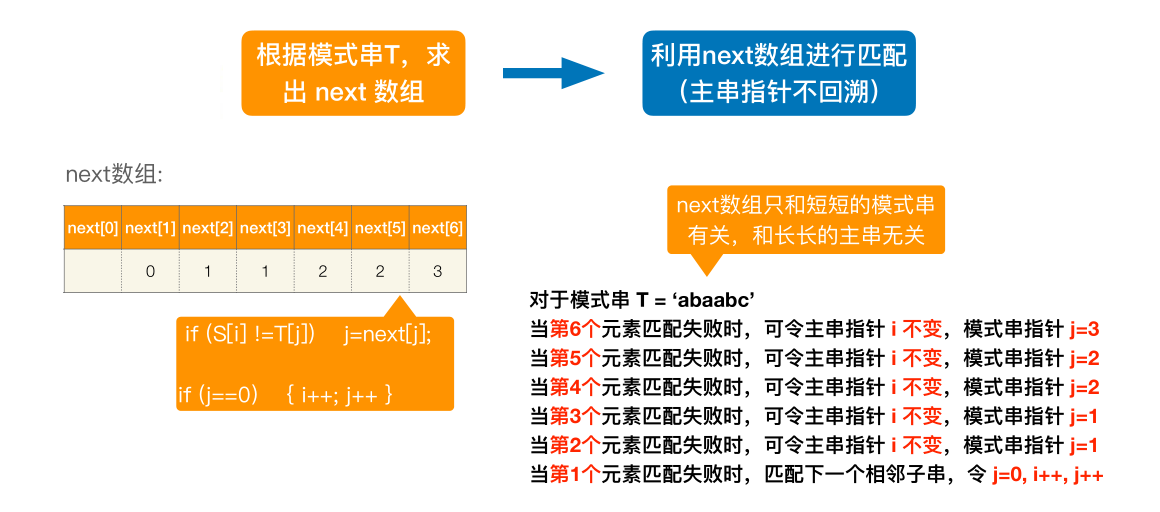
next 数组:

next 数组只和短短的模式串有关,和长的主串⽆关
# KMP 算法
// 求next数组
void get_next(SString S,,int next[]){
int i=1;j=0;
next[1]=0;
while(i<T.length){
if(j==0||T.ch[i]==T.ch[j]){
++i; ++j;
next[i]=j;
} else {
j=next[j];
}
}
}
// kmp算法
int Index_KMP(SString S,SString T,int next[]){
int i=1 , j=1;
while(i<=S.length&&j<T.length){
if(j==0||S.ch[i]==T.ch[j]){
++i;
++j;
} else{
j=next[j];
}
if(j>T.length){
return i-T.length;
} else{
return 0;
}
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
朴素模式匹配 v.s. KMP 算法

KMP 算法精髓:利用好已经匹配过的模式串的信息
# next 数组
# 求模式串的 next 数组(手算练习)
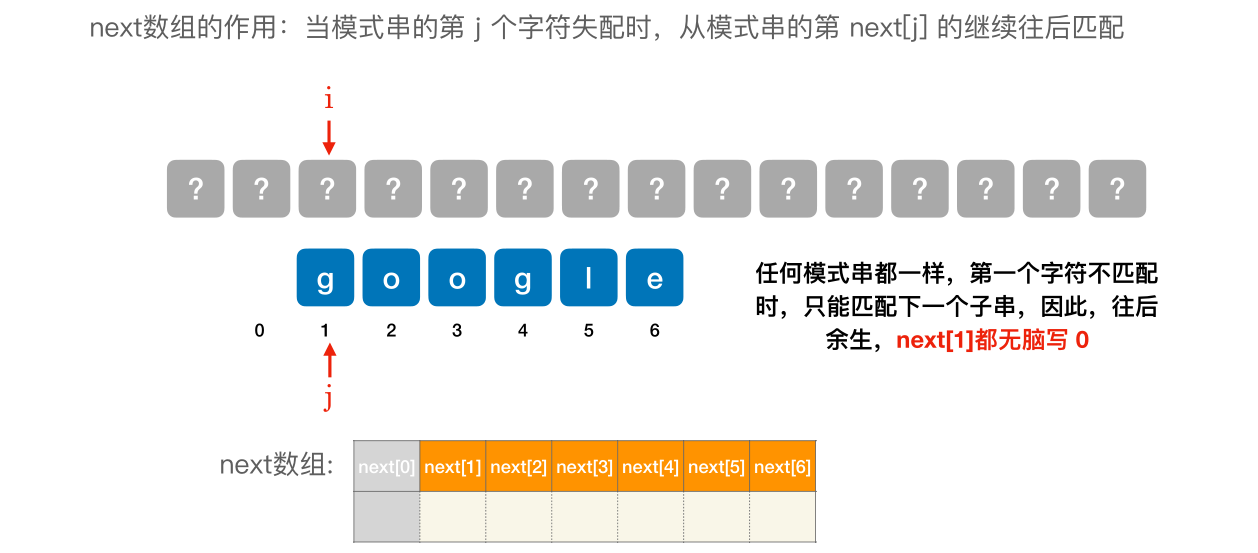
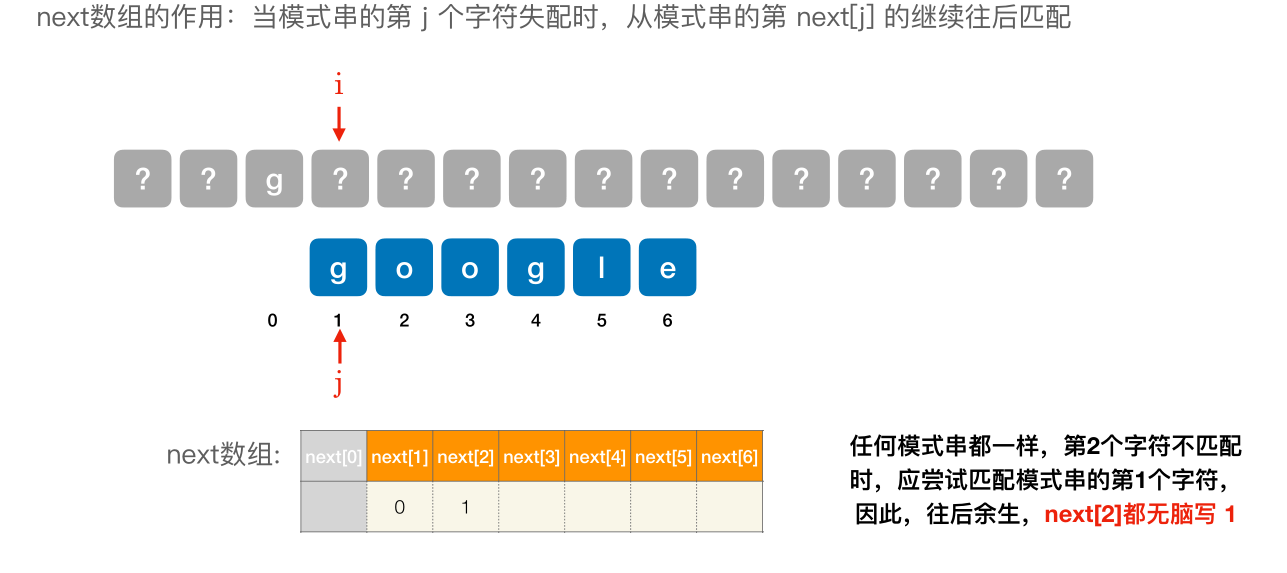
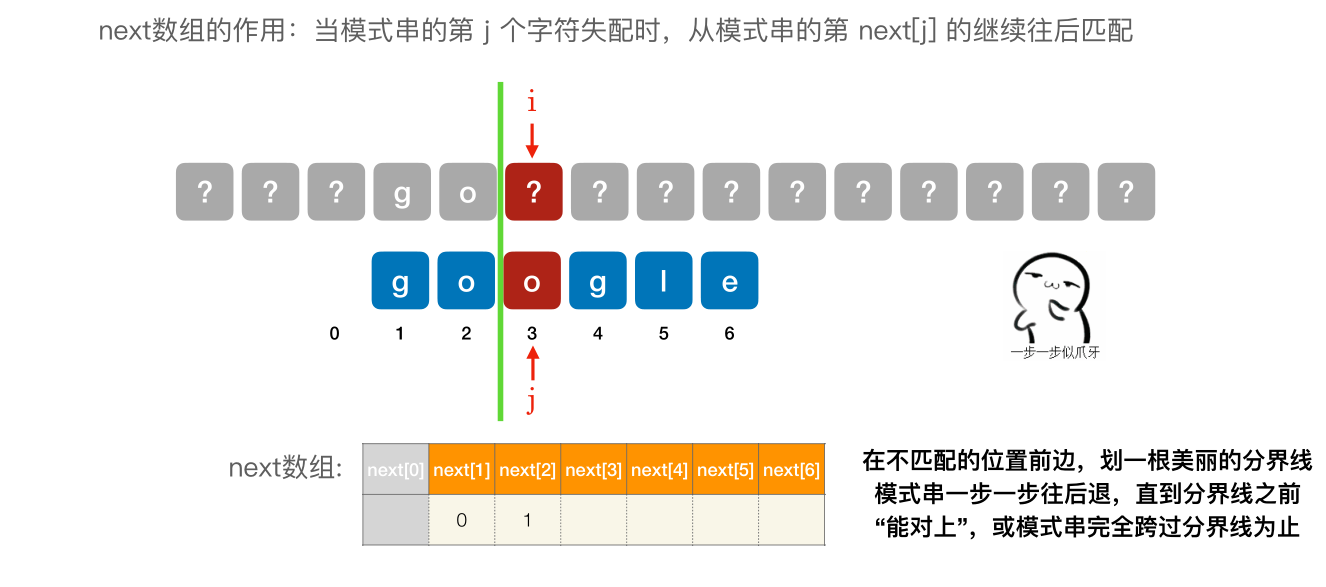
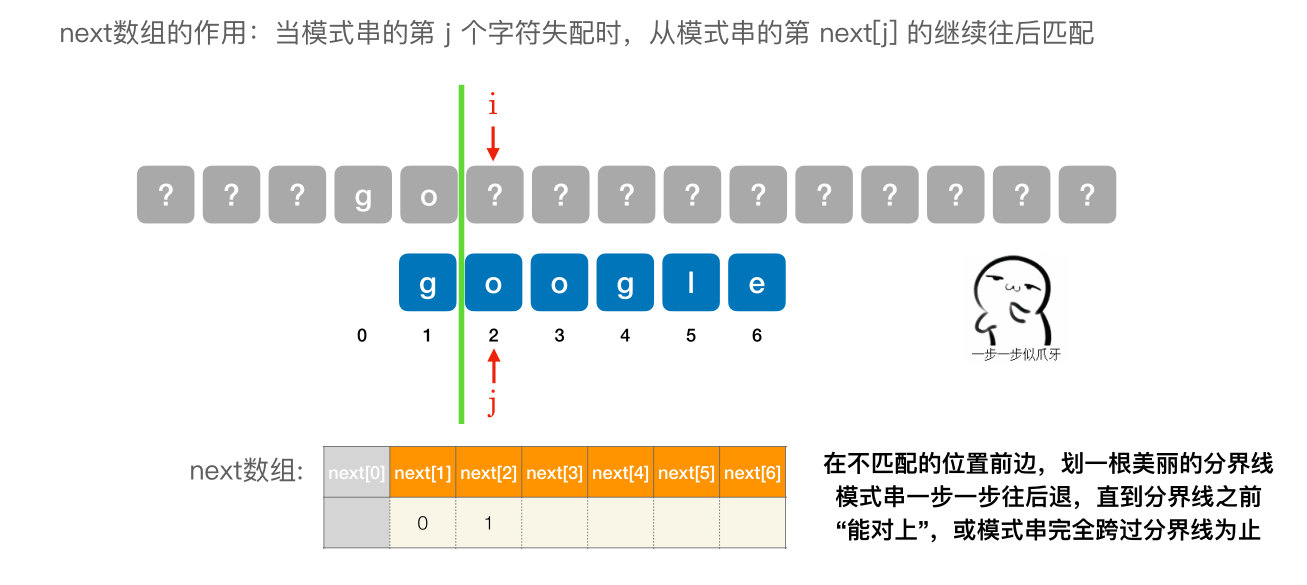
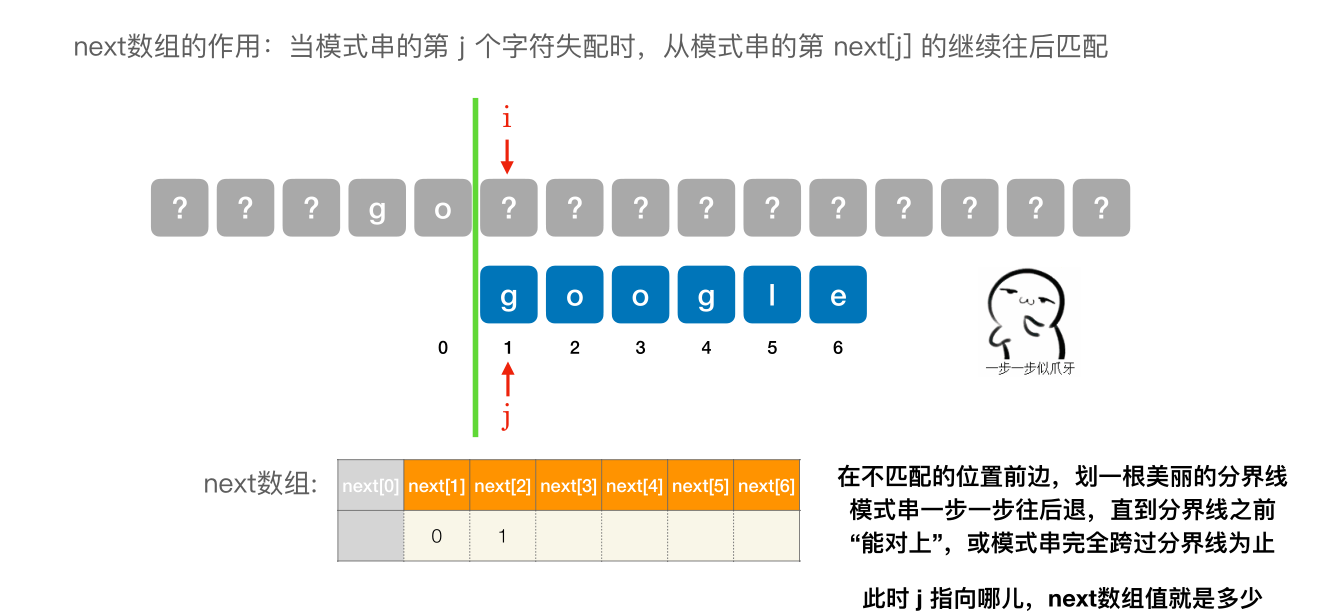
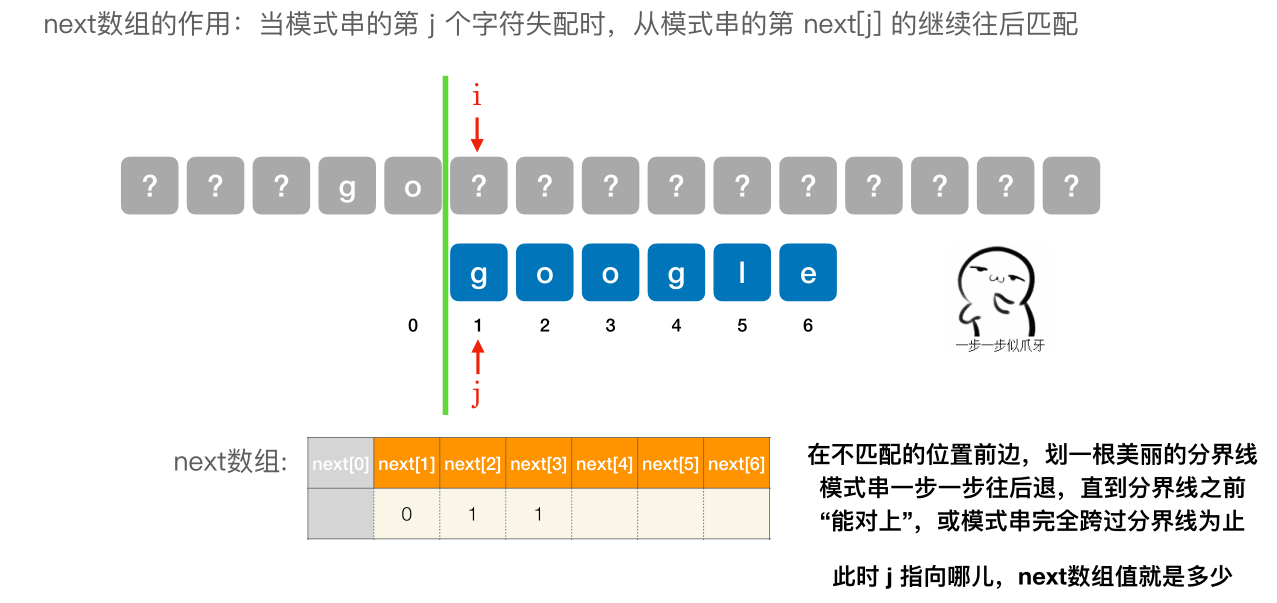
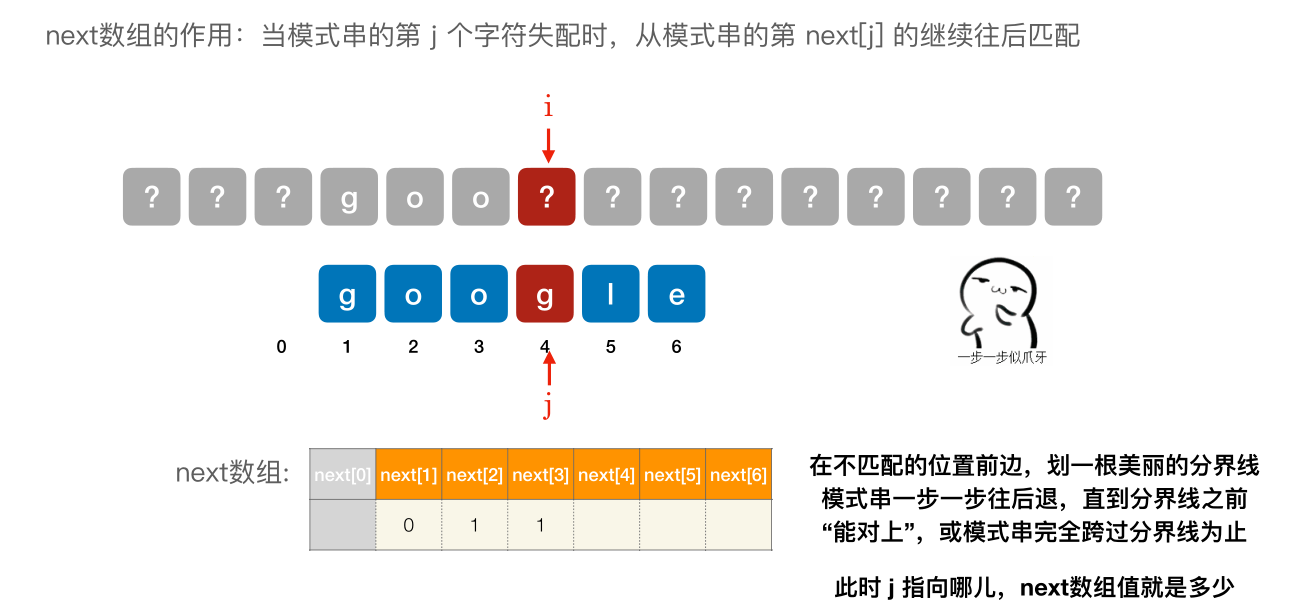
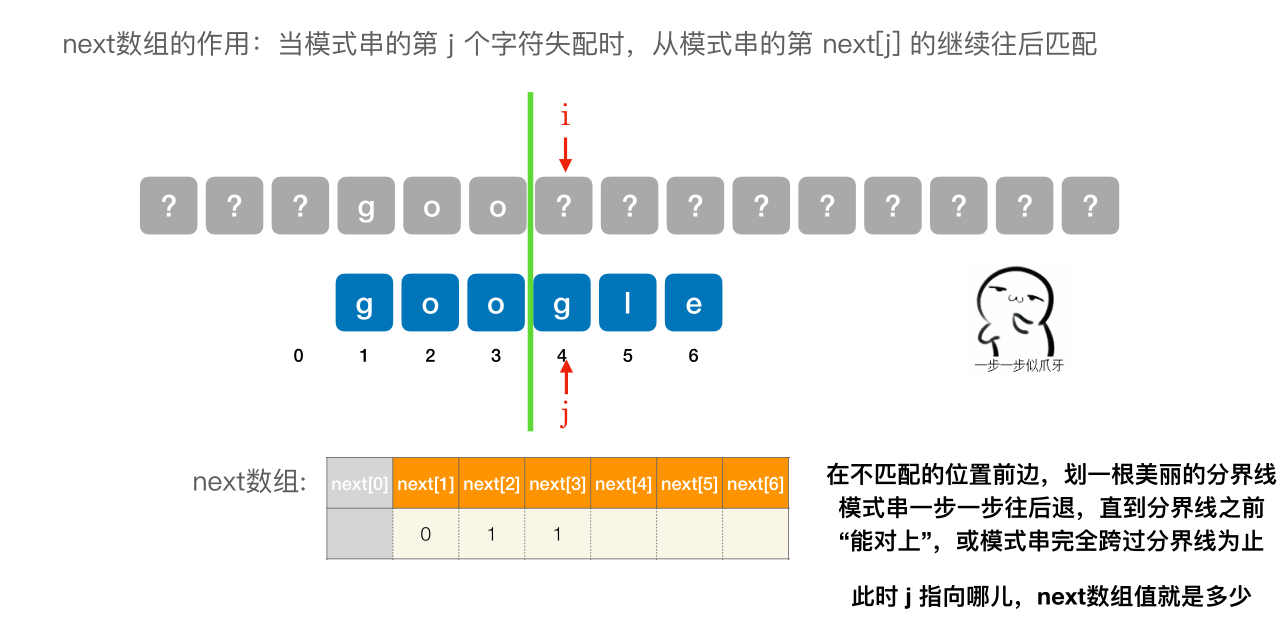
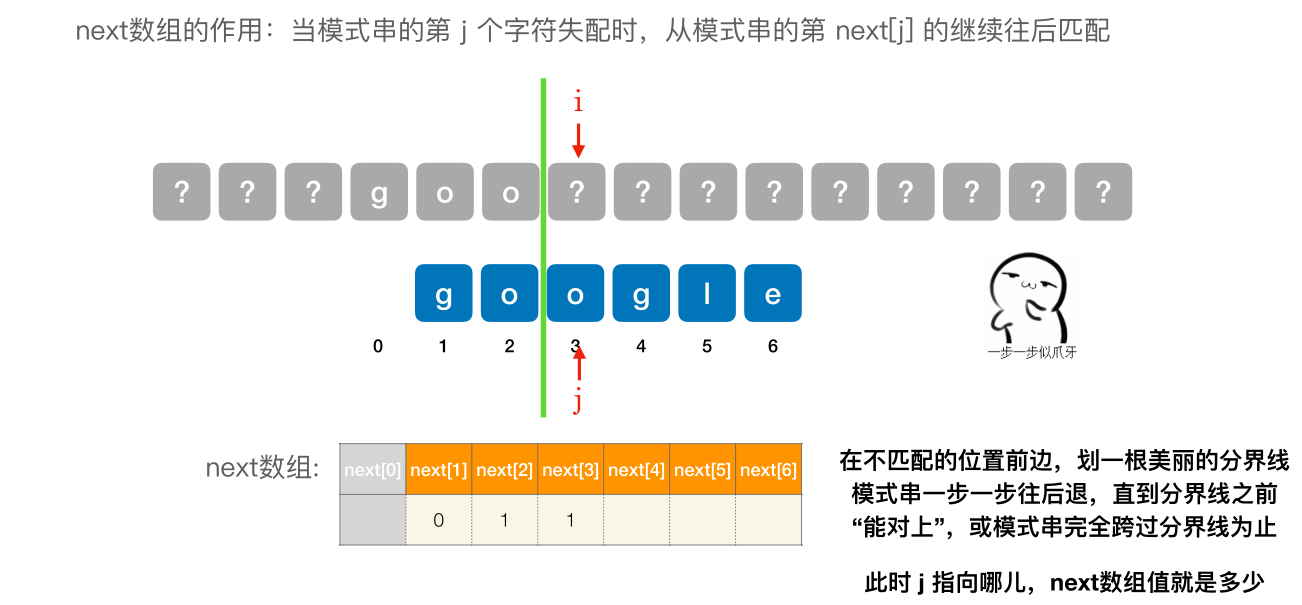
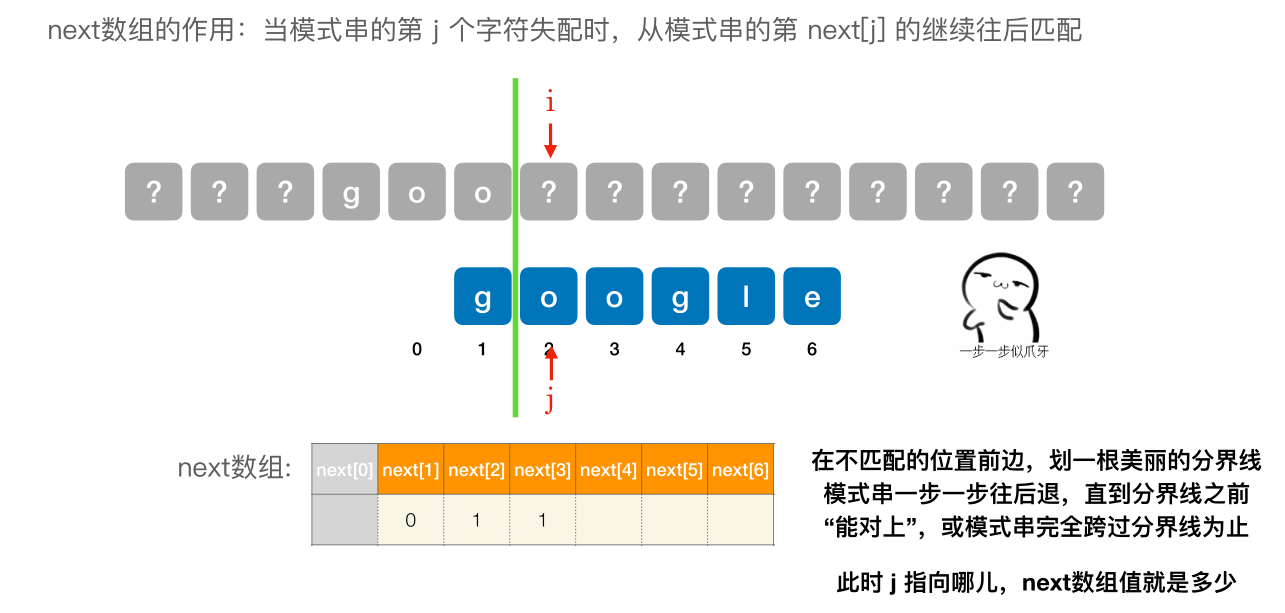
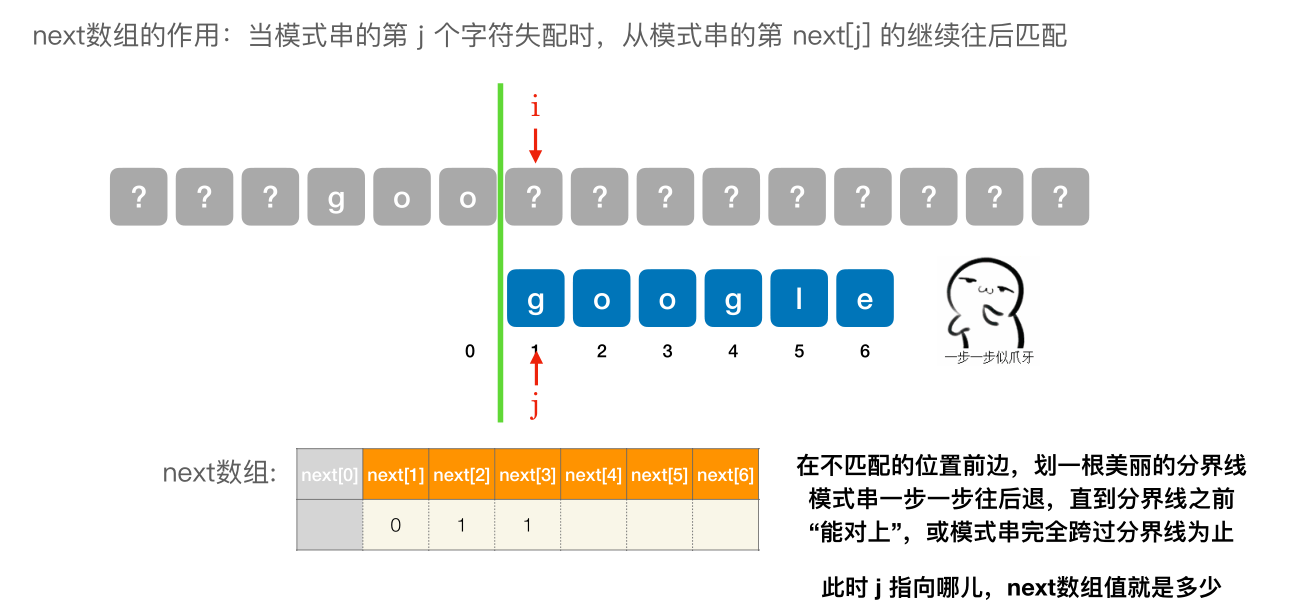
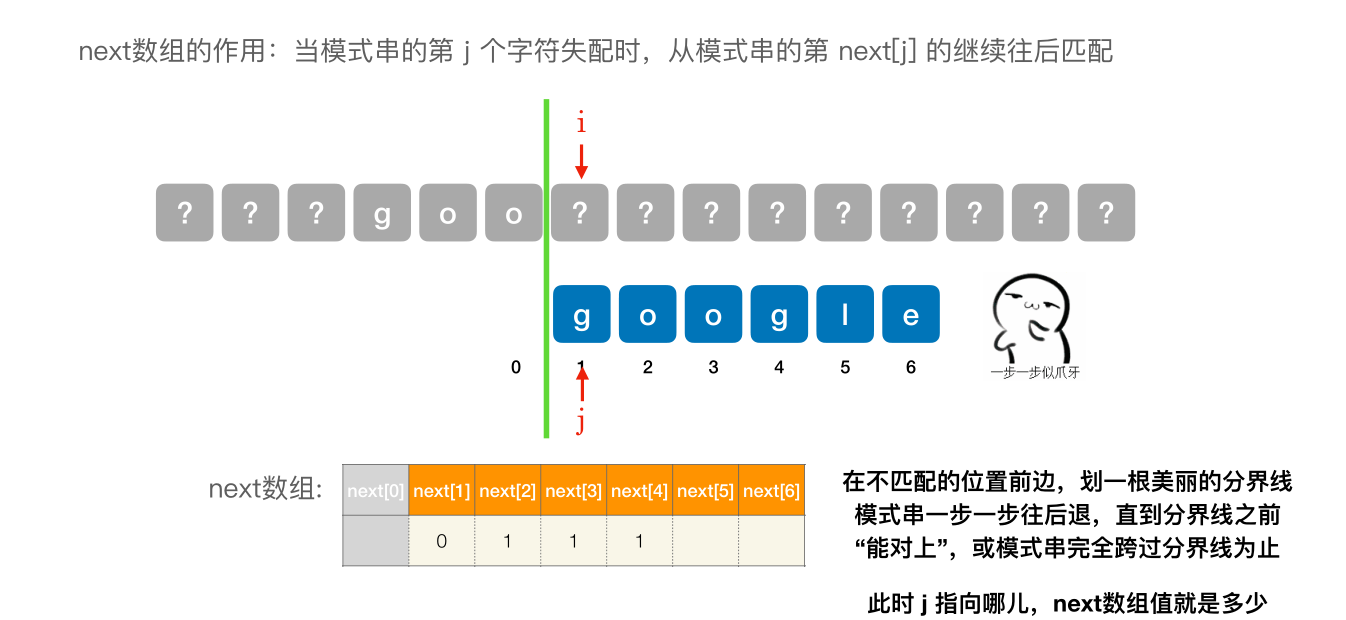
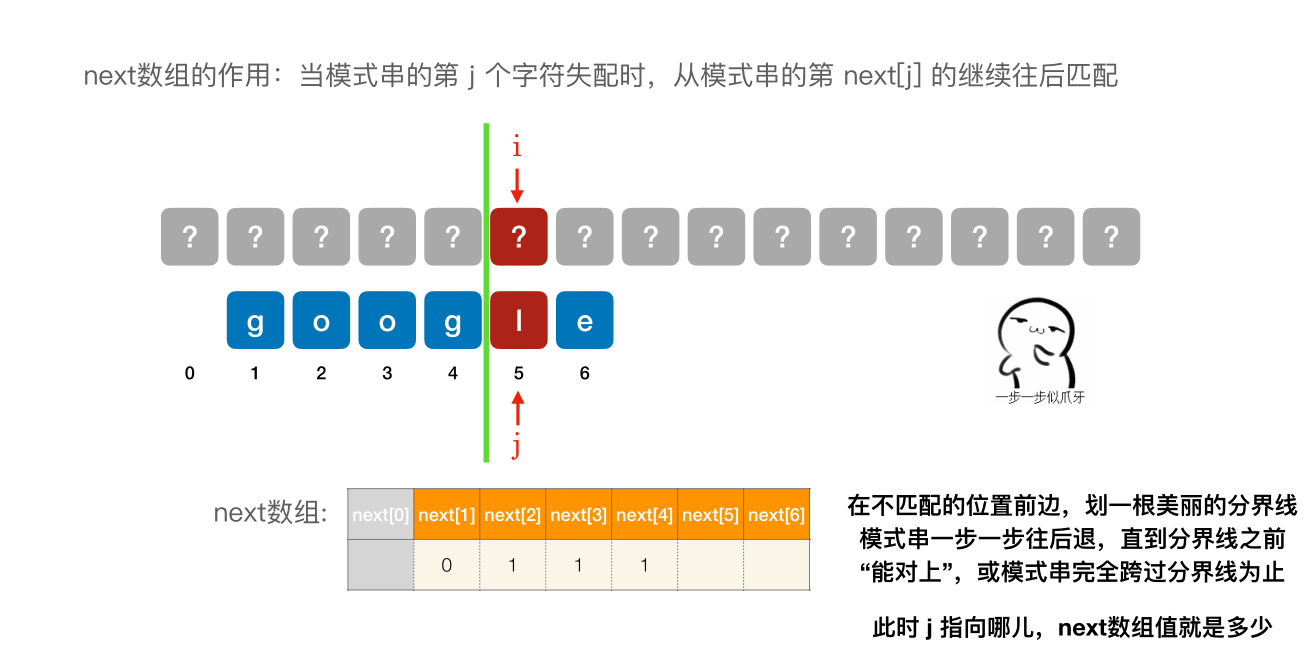
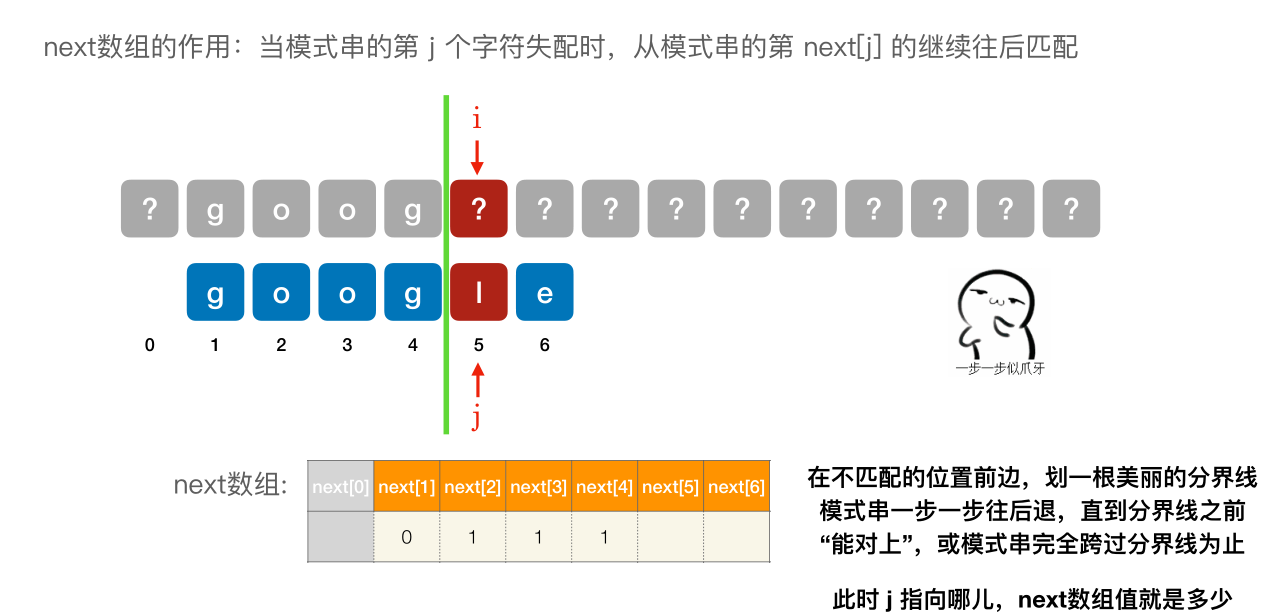
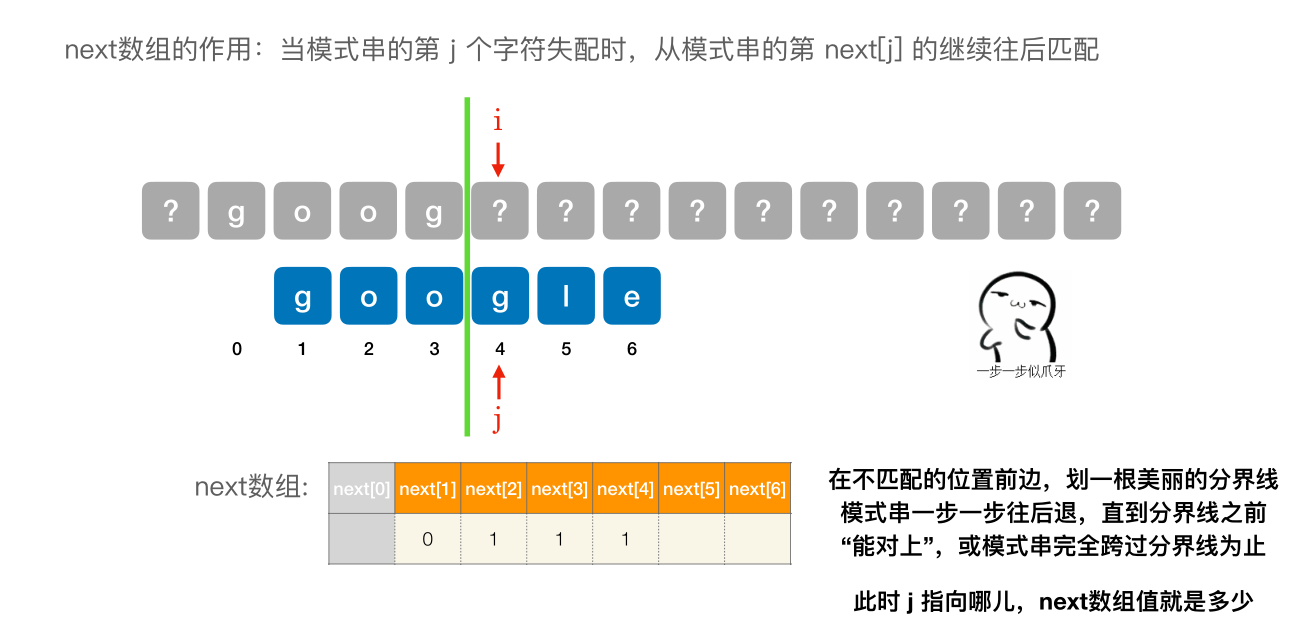
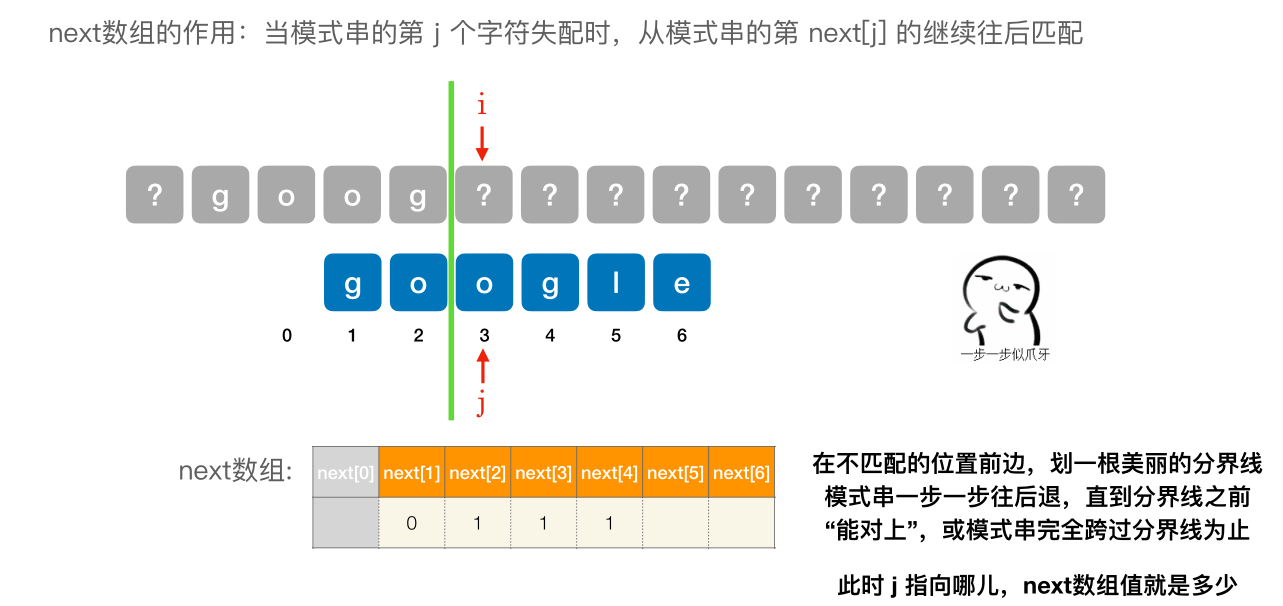
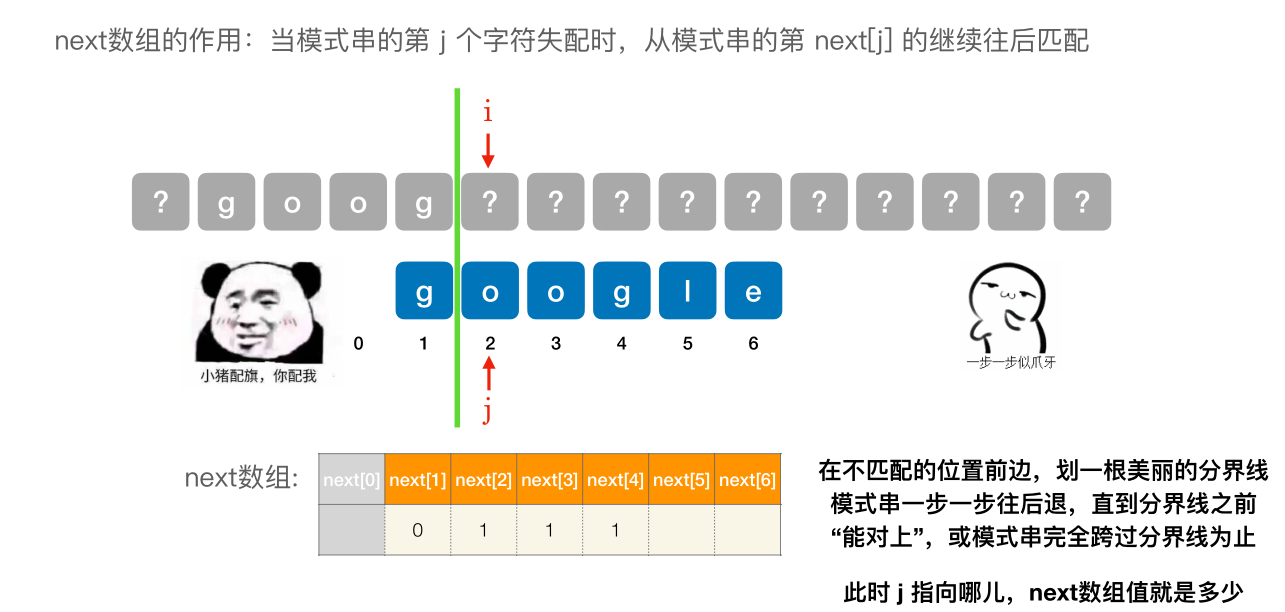
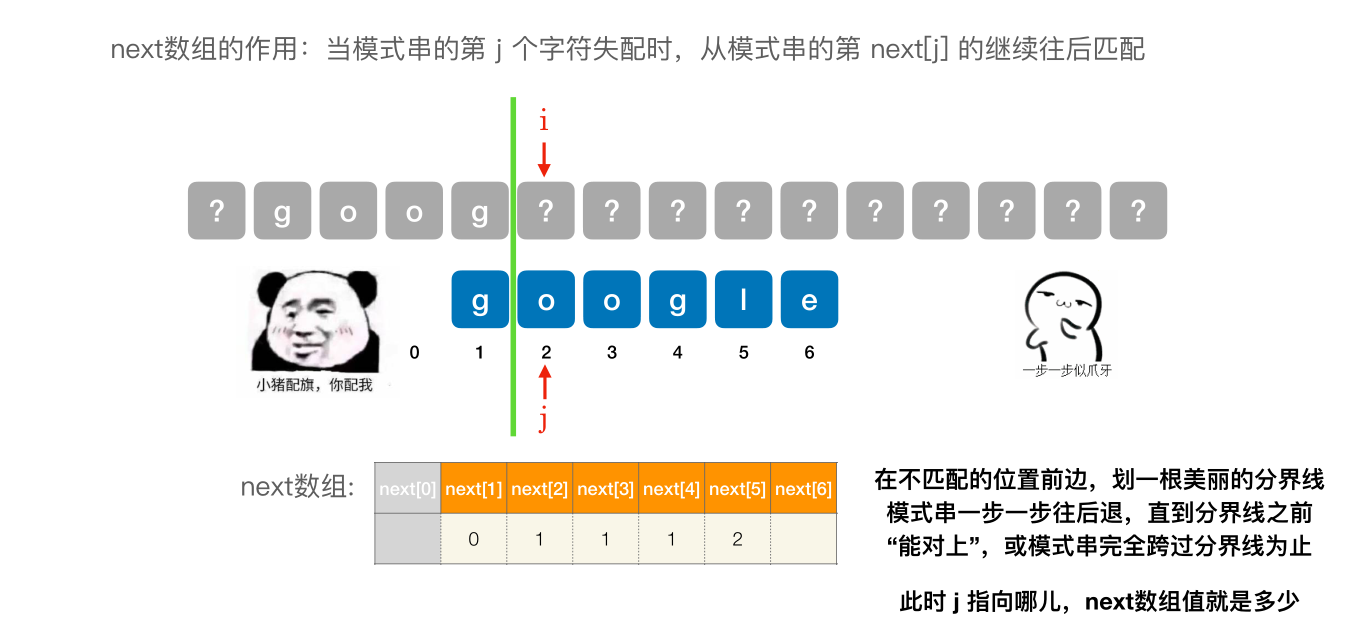
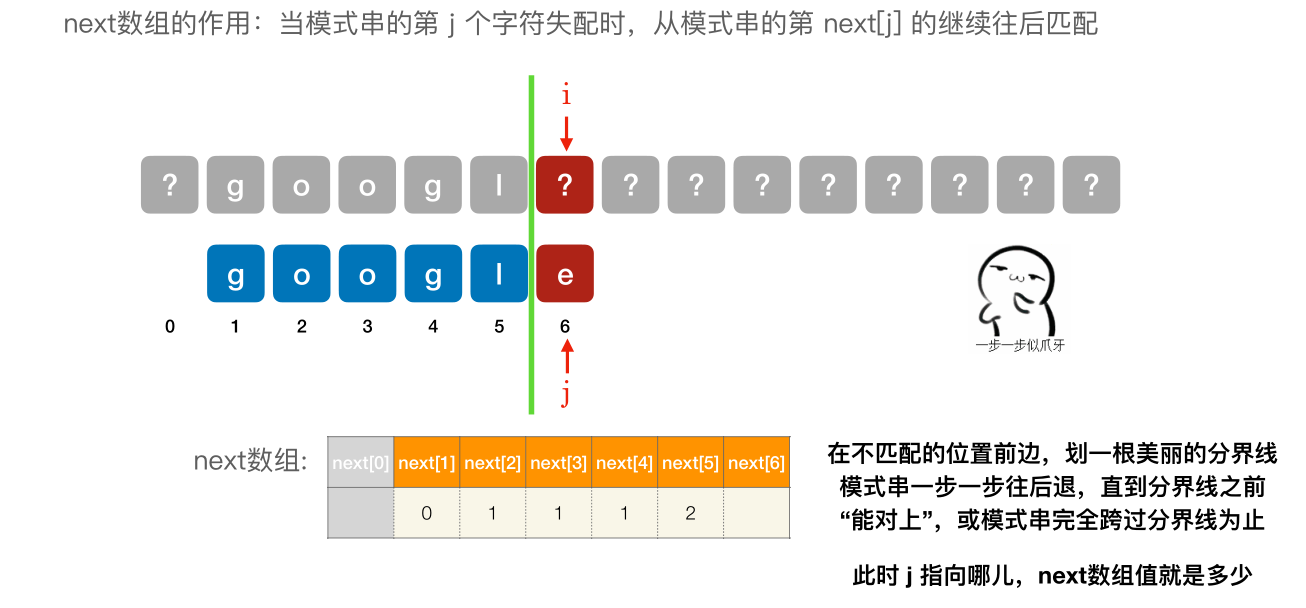
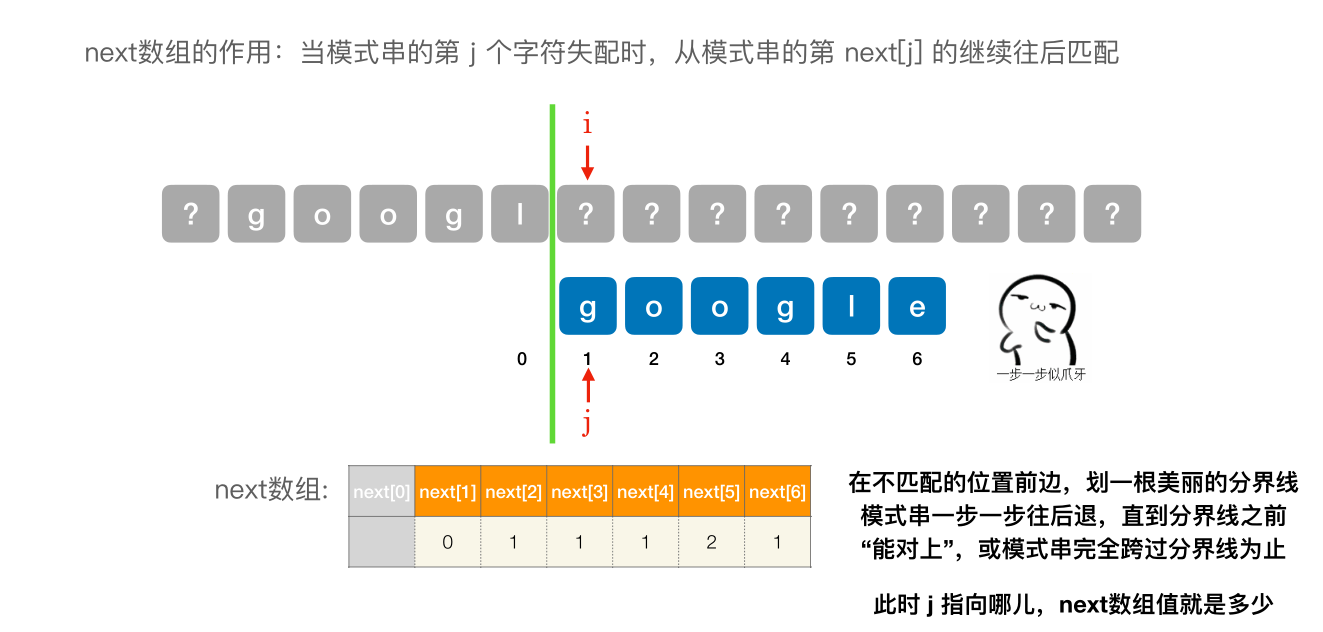
- next [1] 固定为 0
- next [2] 固定 为 1
- 其他的 next 元素,在不匹配的位置前边,划⼀根美丽的分界线模式串⼀步⼀步往后退,直到分界线之前 “能对上”,或模式串完全跨过分界线为止。
# 使用 next 数组进⾏模式匹配
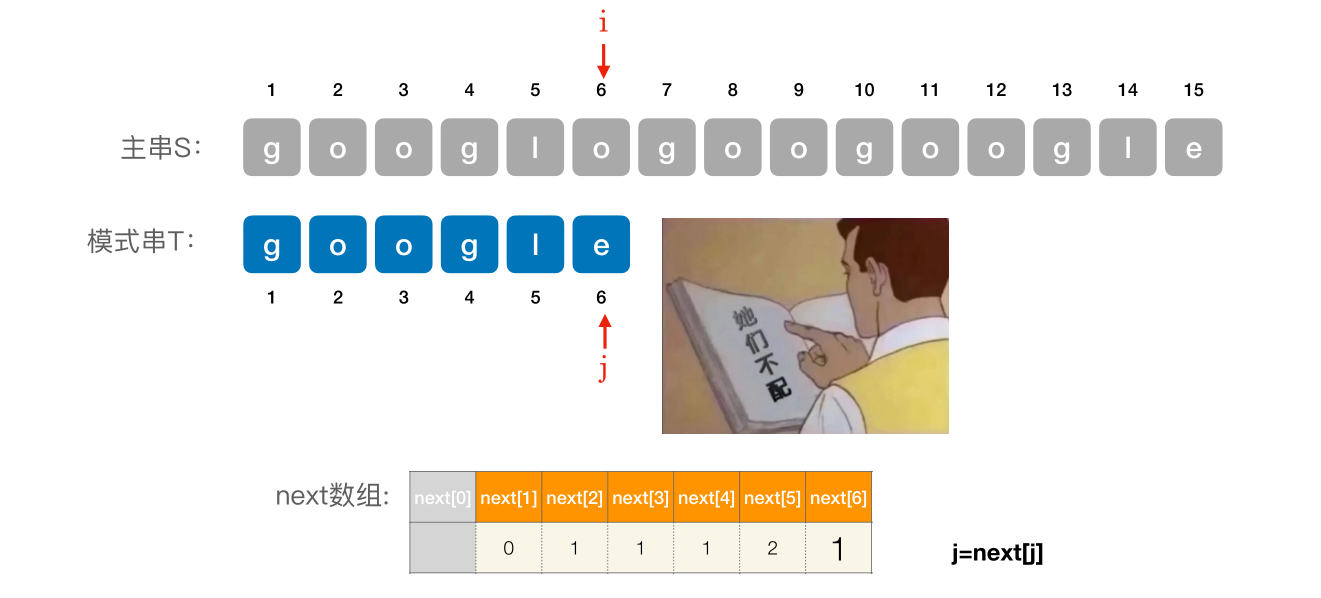
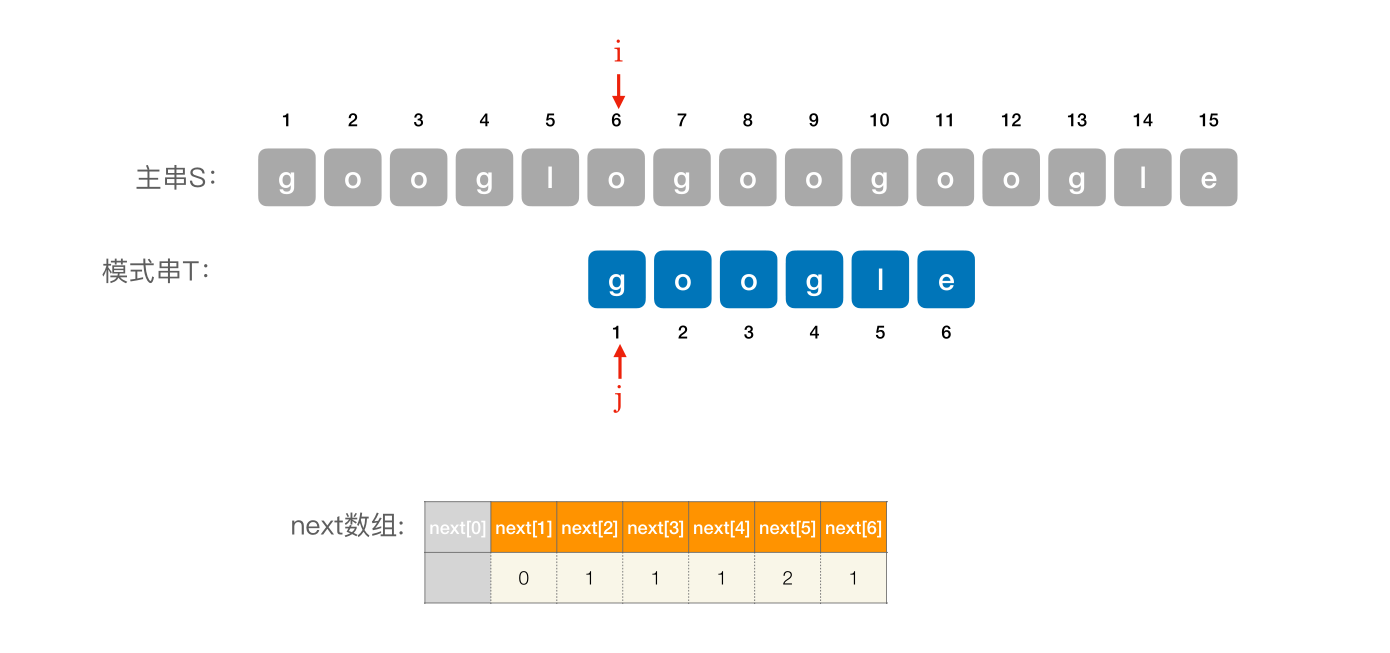
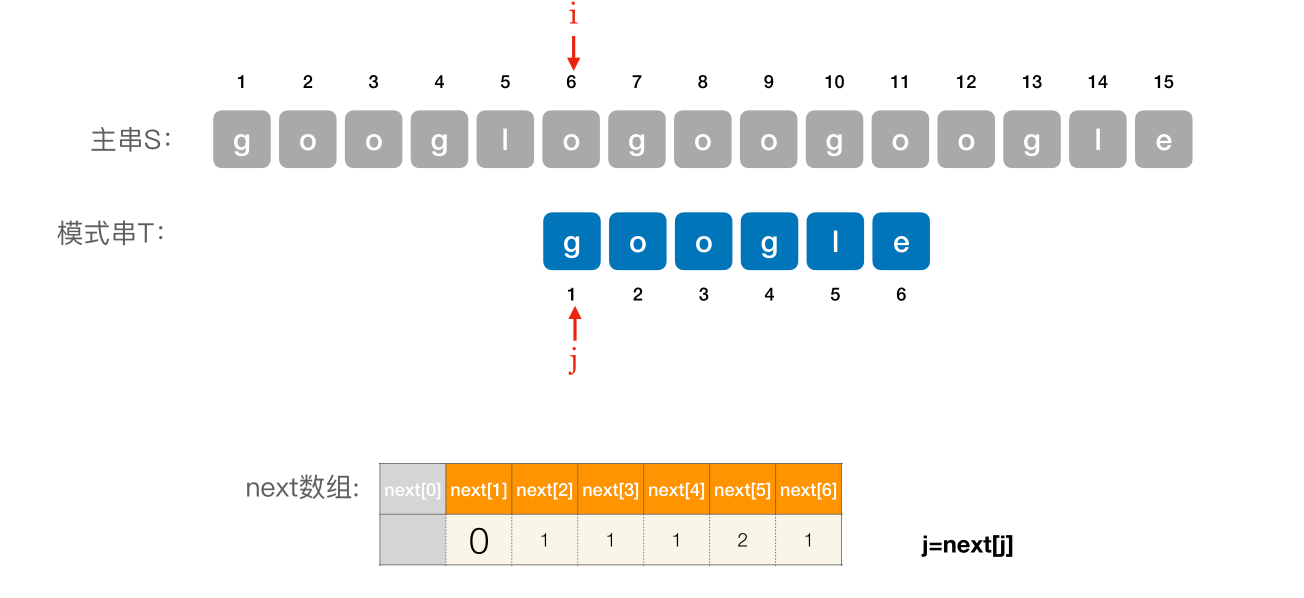
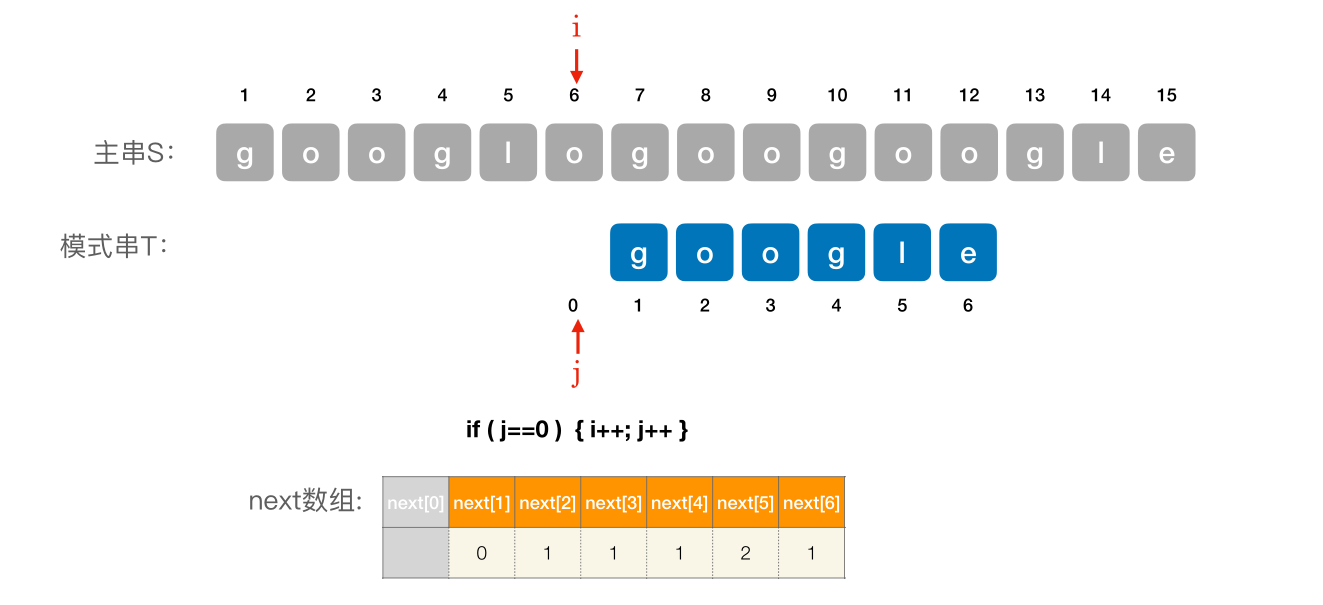
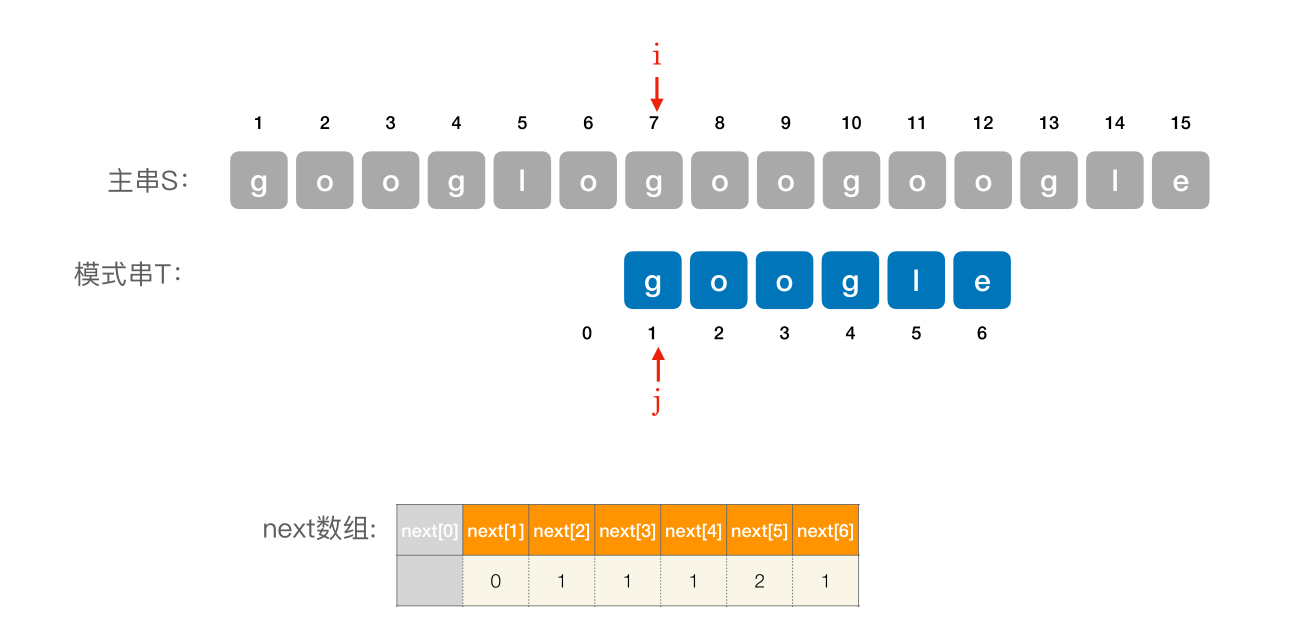

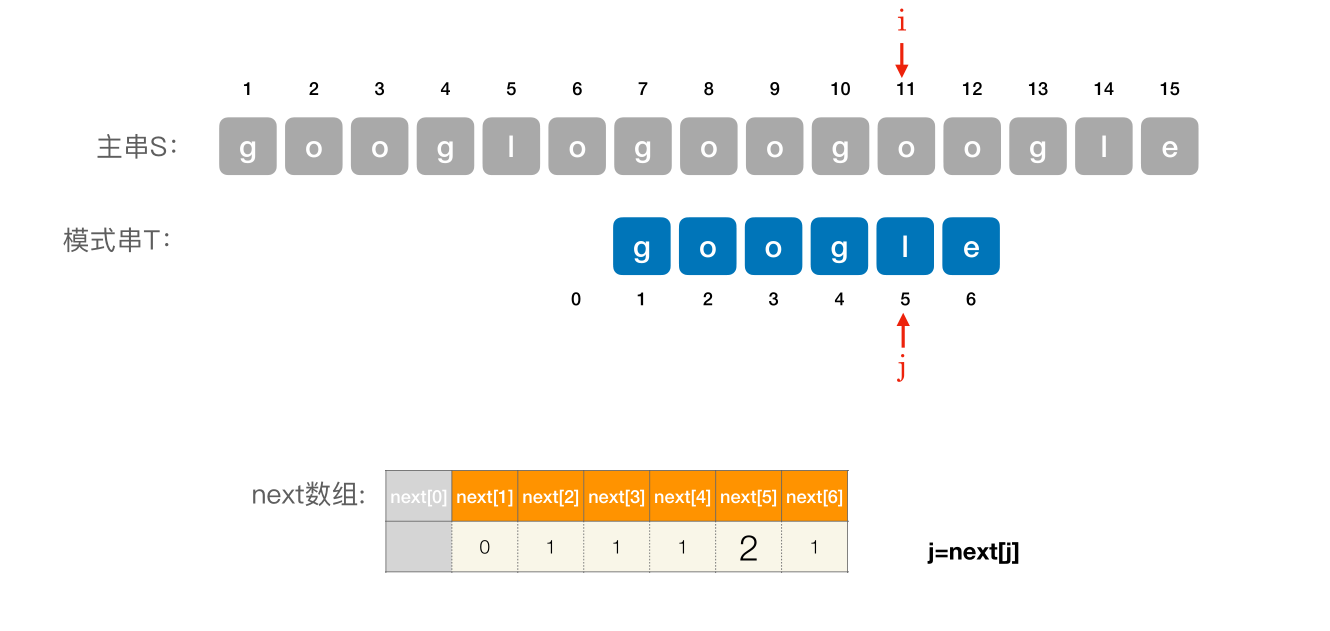
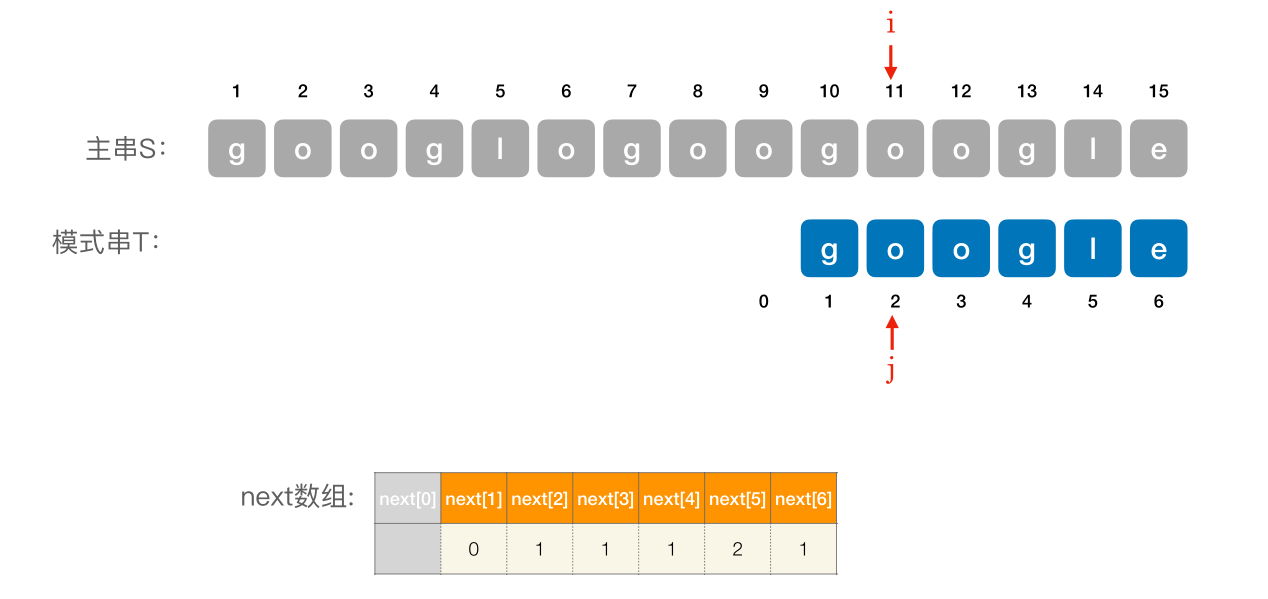
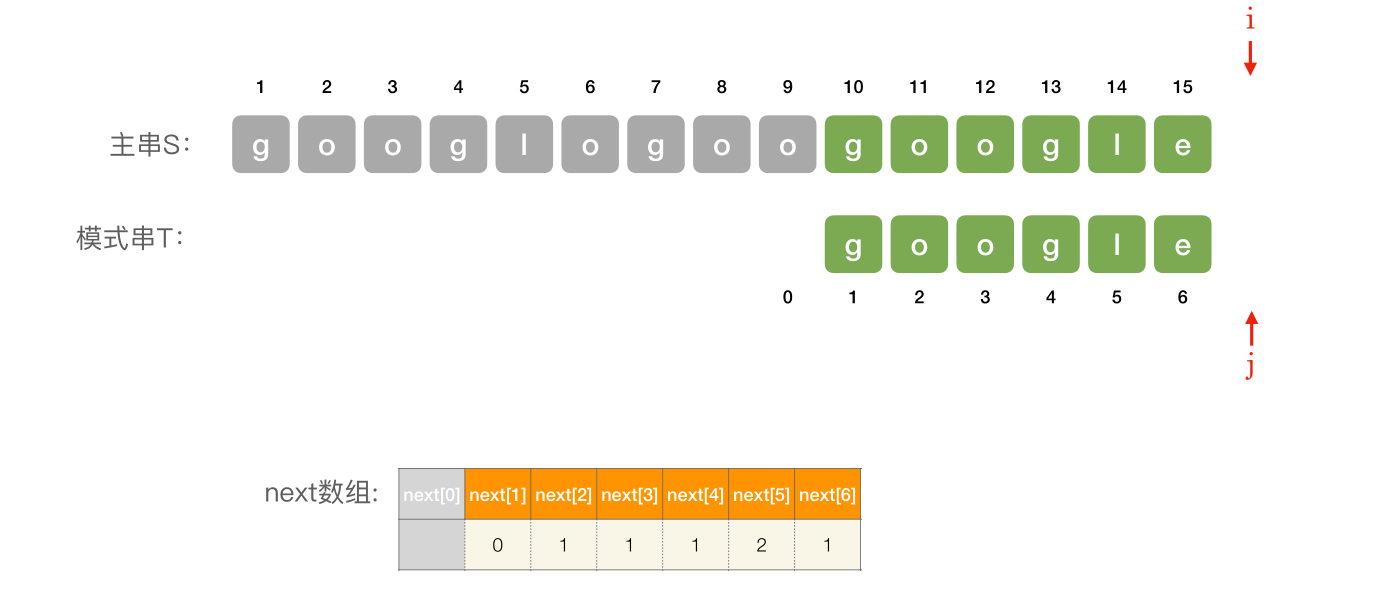
编辑 (opens new window)
上次更新: 2023/12/06, 01:31:48
