数据的表示和运算
数据的表示和运算
# 数据的表示和运算
# 进位计数制
# 最古老的计数方法
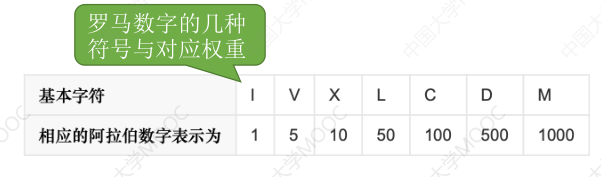
最古老的计数方法 —— 罗马数字

# 十进制计数法
古印度人发明的阿拉伯数字:0,1,2,3,4,5,6,7,8,9。符号反映权重

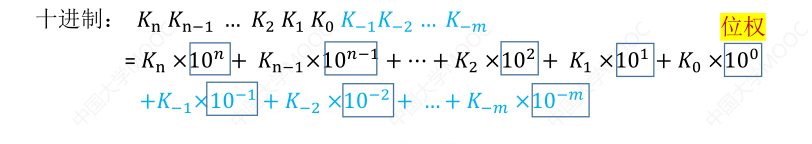
- “进位计数制”:有 0~9,共十种符号。逢十进一
# r 进制计数法
- 基数:每个数码位所用到的不同符号的个数,r 进制的基数为 r
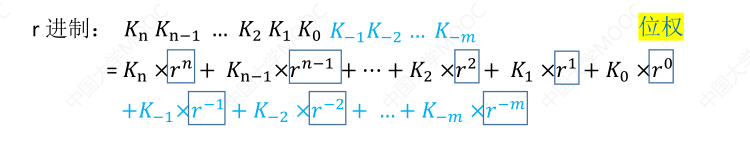

- r 进制的进位计数制,有 0 ~ r-1,共有 r 种符号,逢 r 进 一
二进制是最适合计算机使用的进制,为什么呢?
- 可使用两个稳定状态的物理器件表示,如高电平低电平,电荷正负性等
- 0,1 正好对应逻辑值 假、真。方便实现逻辑运算
- 可很方便地使用逻辑门电路实现算术运算
# 不同进制数之间的相互转换
# 任意进制转十进制

# 二进制与八进制互转
二转八,3 位一组,毎组转换成对应的八进制符号,如不足三位则需要在后面 / 前面补足零

八转二,每位八进制对应的 3 位二进制
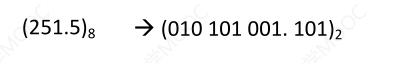
# 二进制与十六进制互转
二转十六,4 位一组,毎组转换成对应的十六进制符号,如不足三位则需要在后面 / 前面补足零
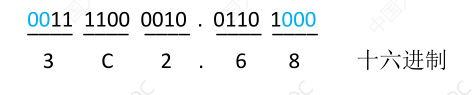
十六转二,每位十六进制对应的 4 位二进制
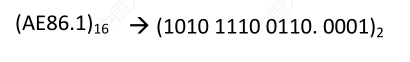
# 各种进制的常见书写方式

# 十进制转任意进制
我们用 r 进制除以 r,可以得到一个余数
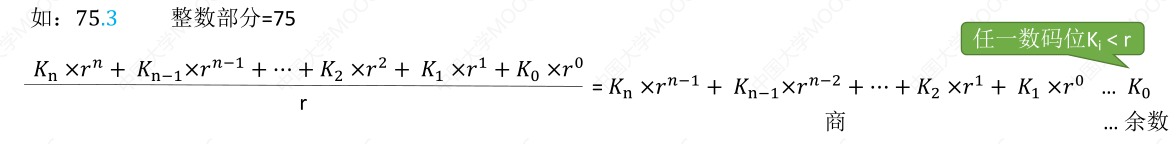

那么小数部分怎么处理呢,我们可以用小数部分乘以基数 r,而前面的整数就是我们要的二进制在各个位上的值,称为乘基取整法,注意有的十进制小数无法用二进制精确表示,如下面例子中的 0.3
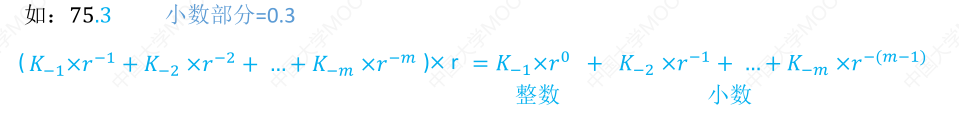

# 拼凑法

十进制:260.75、533.125
# 真值和机器数
- 真值:符合人类习惯的数字
- 机器数:数字实际存到机器里的形式,正负号需要被 “数字化”

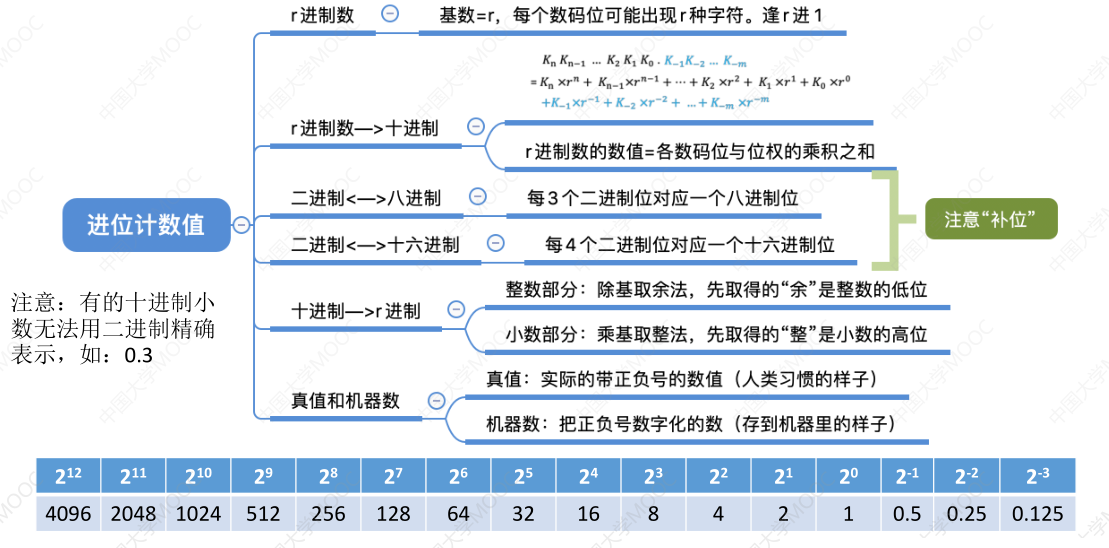
# 总结
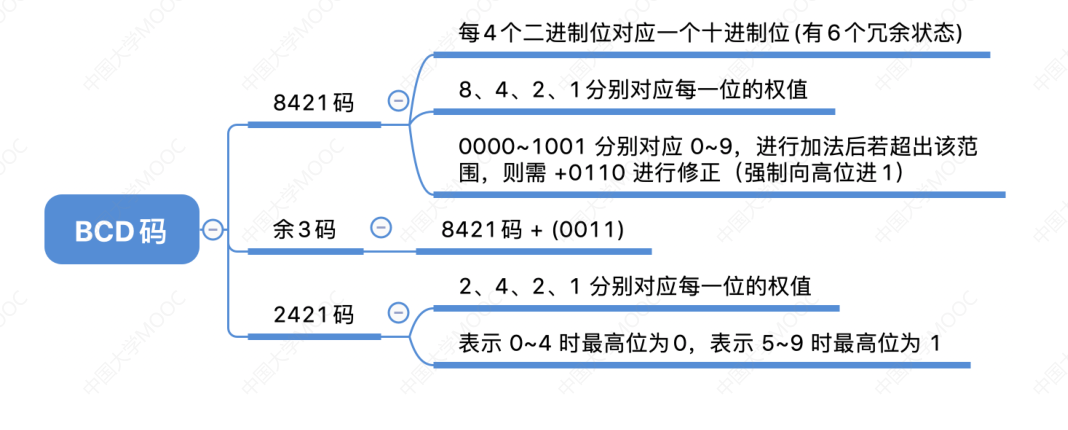
# BCD 码
BCD :Binary-Coded Decimal,用二进制编码的十进制
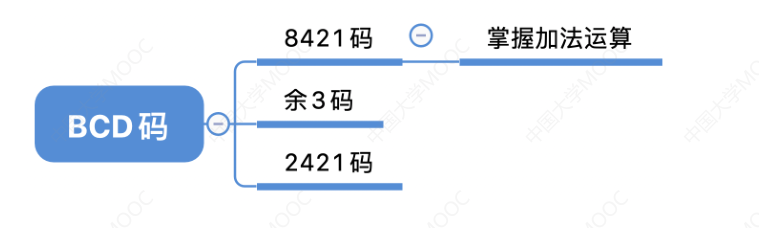
# 8421 码
8421 码指的是 4 位来描述,它是一种有权码,从高到低依次为 8,4,2,1
4 个二进制位 —> 16 种不同的状态,而 BCD 码直使用其中 10 种 —> 不同的映射方案


若两个 8421 码相加之和小于或等于
若 相加之和大于或等于

# 余 3 码
余 3 码:8421 码 +

# 2421 码
2421 码:改变权值定义,这也是一种有权码,权值由高到低分别为 2,4,2,1,特点是大于或等于 5 的 4 位二进制数中最高位为 1,小于 5 的最高位为 0,为了避免歧义出现两种有权码的情况

# 总结
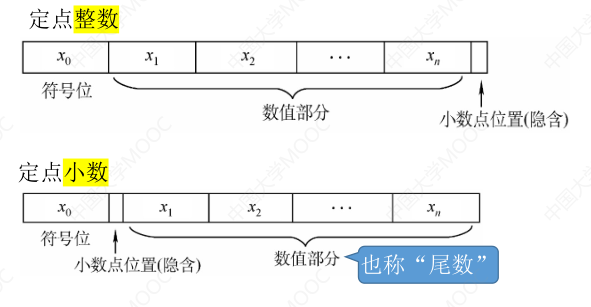
# 定点数的编码表示
- 定点数:小数点的位置固定 Eg:996.007 —— 常规计数
- 浮点数:小数点的位置不固定 Eg:
—— 科学计数法
# 无符号数的表示
- 无符号数:整个机器字长的全部二进制位均为数值位,没有符号位,相当于数的绝对值。
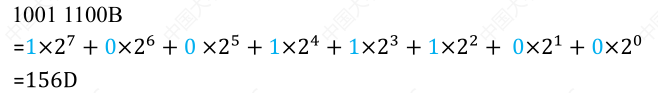
表示范围

通常只有无符号整数,而没有无符号小数
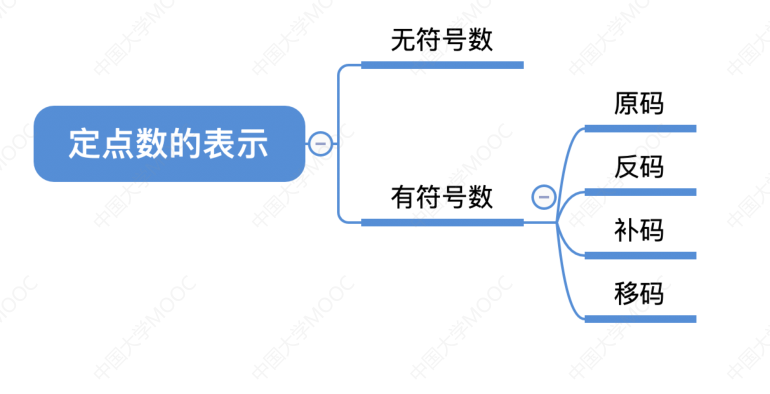
# 有符号数的定点表示

# 原码
- 原码:用尾数表示真值的绝对值,符号位 “0/1” 对应 “正 / 负”
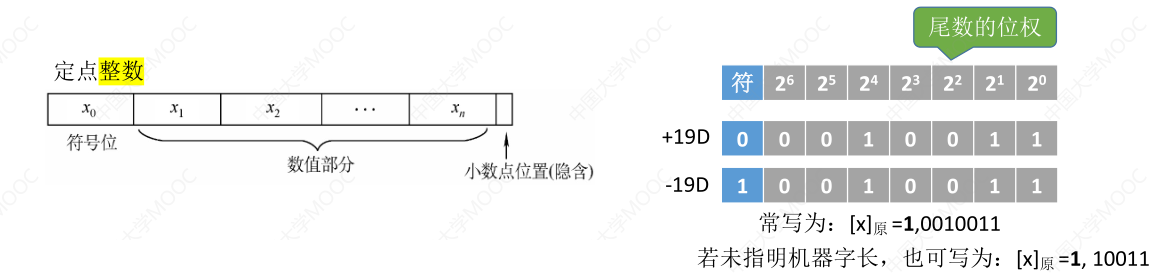

- 若机器字长 n+1 位,原码整数的表示范围:
(关于原点对称),真值 0 有 +0 和 -0 两种形式 - 若机器字长 n+1 位,原码小数的表示范围:
(关于原点对称),真值 0 有 +0 和 -0 两种形式
# 反码
- 若符号位为 0,则反码与原码相同
- 若符号位为 1,则数值位全部取反
“反码” 只是 “原码” 转变为 “补码” 的一个中间状态


# 补码
- 正数的补码 = 原码
- 负数的补码 = 反码末位 + 1(要考虑进位)

将负数补码转回原码的方法相同:尾数取反,末位 + 1

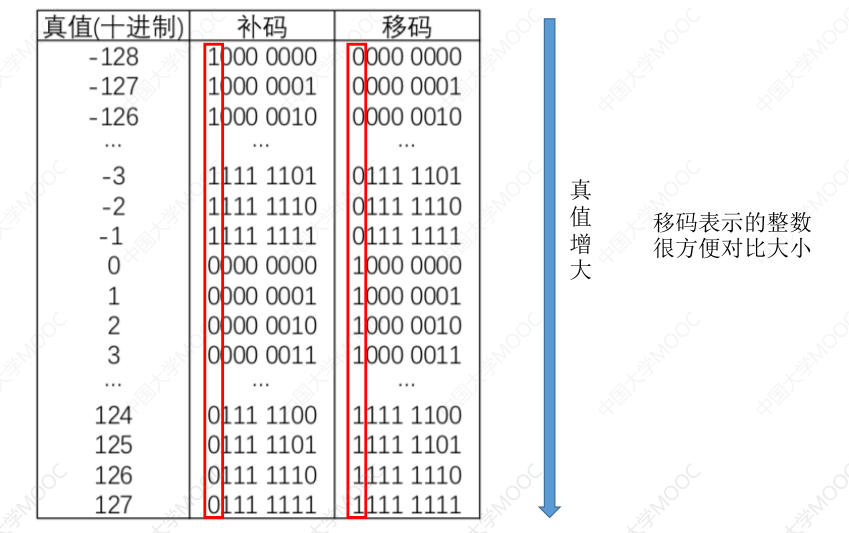
# 移码
- 补码的基础上将符号位取反。注意:移码只能用于表示整数


用移码表示的整数可以很方便对比大小,我们首先比对第一位,如果相同则往后继续对比
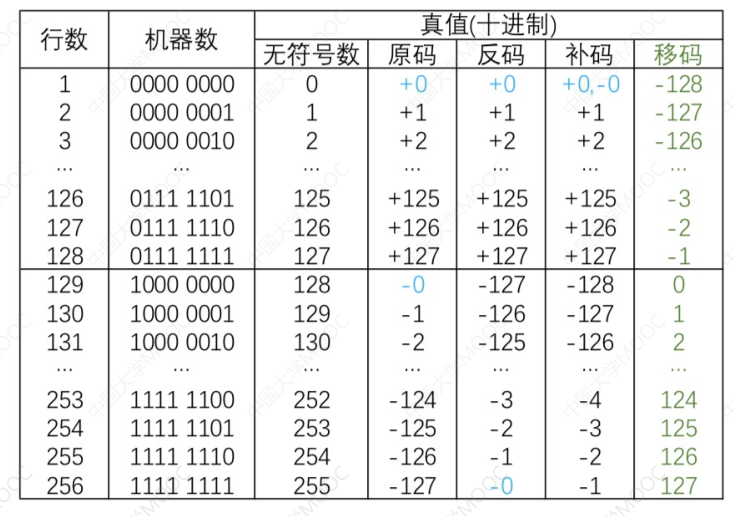
# 用几种码表示定点整数
- 原码和反码的真值 0 有两种表示
- 补码和移码的真值 0 只有一种表示
- 补码和移码可以多表示一个负数
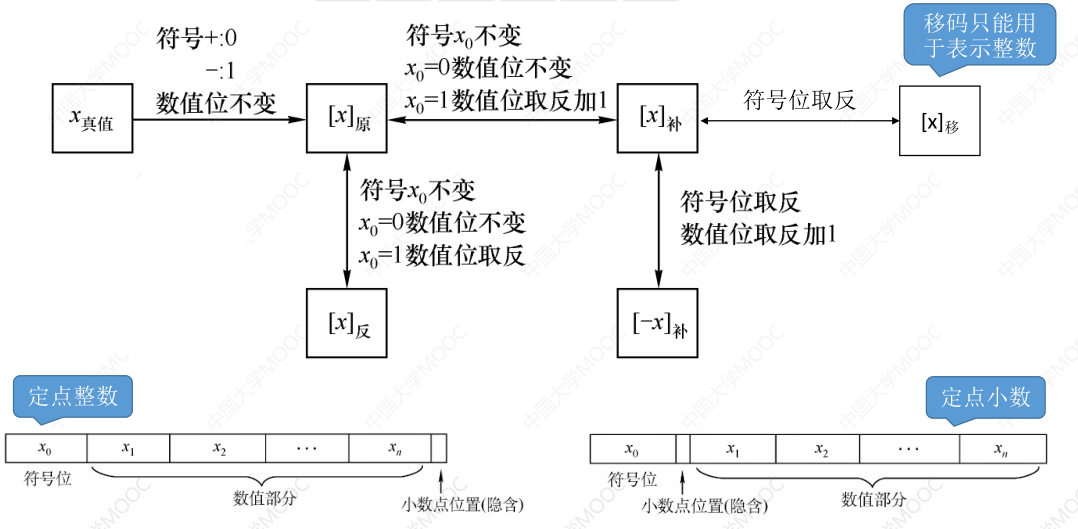
# 总结
- 由
快速求 $[-x]_补 $:可以将符号位、数值位全部取反,末位 + 1

# 各种码的作用
# 加减运算
有符号数和无符号数在加运算时的差异

如果是有符号数则需要转为减法

使用原码运算:
- 加法 —— 用加法器完成
- 减法 —— 用减法器完成
# 用加法代替减法
当一个时钟指向 10 点时,我们想更改时钟为 7 点,则有两种方式,顺时针和逆时针,顺时针可以看作加法运算,而逆时针可以看作为逆时针,由于时钟的时针的范围是 12,所以在模 12 的情况下,我们可以将减法运算替换成相当于的加法运算
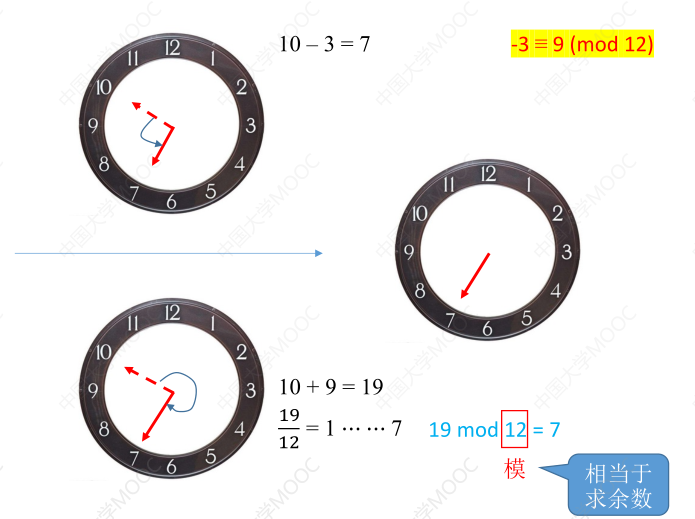
# 模运算的性质



如:
# 计算机底层如何实现这个操作
我们限制每个数使用 8bit 的空间,所以任何运算结果在

- 补码的作用:使用补码可将减法操作转变为等价的加法,ALU 中无需集成减法器。执行加法操作时,符号位一起参与运算
# 浮点数的表示和运算
# 浮点数的表示
# 定点数的局限性
定点数可表示的数字范围有限,但我们不能无限制地增加数据的长度
如何在位数不变的情况下增加数据表示范围?
从科学计数法理解浮点数
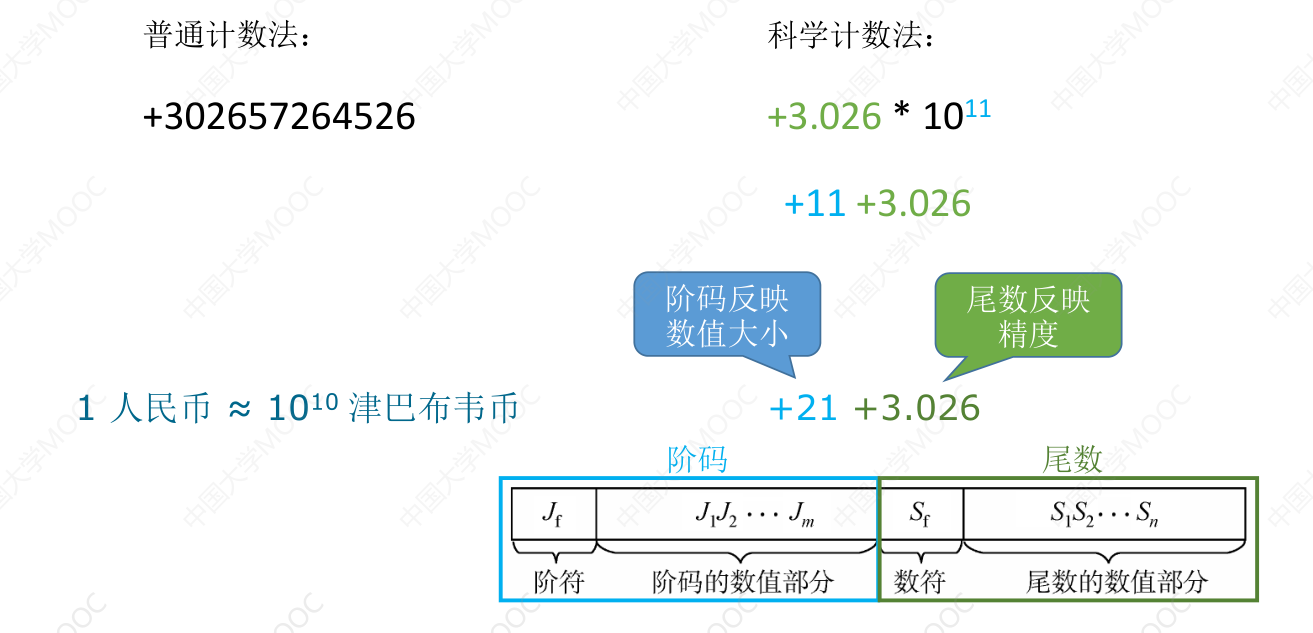
# 浮点数的表示
定点数:如纯小数 0.1011 和纯整数 11110

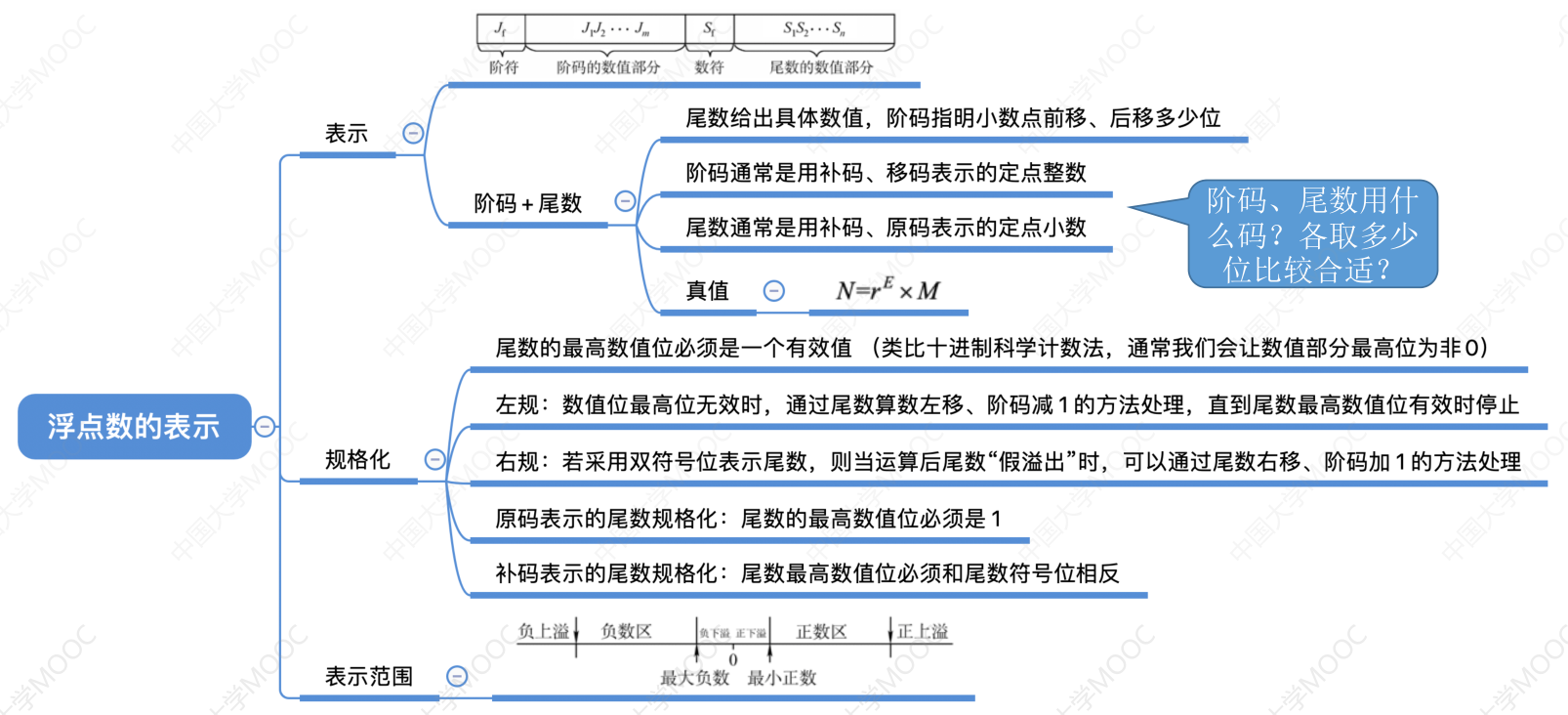
- 阶码 E 反映浮点数的 表示范围 及小数点的实际位置;
- 尾数 M 的数值部分的位数 n 反映浮点数的 精度 。
尾数给出一个小数,阶码指明了小数点要向前 / 向后移动几位。


# 浮点数尾数的规格化
如果 b 使用 8bit 的存储空间存储,那么会丢失部分精度,如科学计数法中的尾数的最高位是无效值,会丧失精度

以上面的 b 为例子,我们可以将尾数向左移,不以 0 为开头的无效值存储
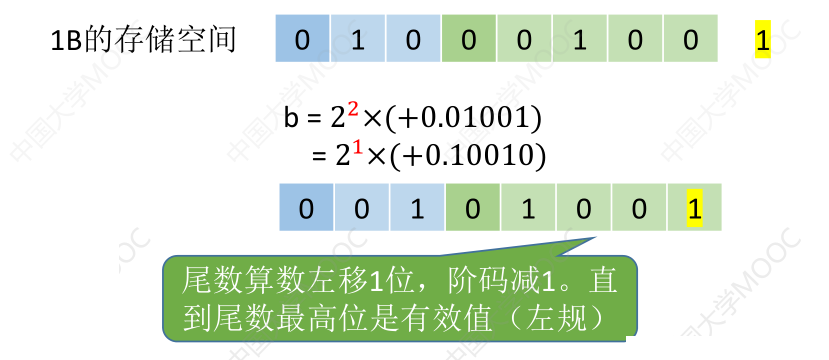
规格化浮点数:规定尾数的最高数值位必须是一个有效值 。
- 左规:当浮点数运算的结果为非规格化时要进行规格化处理,将尾数算数左移一位,阶码减 1。
- 右规:当浮点数运算的结果尾数出现溢出(双符号位为 01 或 10)时,将尾数算数右移一位,阶码加 1。

注:采用 “双符号位” ,当溢出发生时,可以挽救。更高的符号位是正确的符号位
# 规格化浮点数的特点
用原码表示的尾数进行规格化:
- 正数为 0.1××…× 的形式,其最大值表示为 0.11…1;最小值表示为 0.10…0。尾数的表示范围为 1/2≤M≤(1−2 −n)。
- 负数为 1.1××…× 的形式,其最大值表示为 1.10…0;最小值表示为 1.11…1。尾数的表示范围为−(1−2 −n)≤M≤−1/2。
用补码表示的尾数进行规格化:
- 正数为 0.1××…× 的形式,其最大值表示为 0.11…1;最小值表示为 0.10…0。尾数的表示范围为 1/2≤M≤(1−2 −n)。
- 负数为 1.0××…× 的形式,其最大值表示为 1.01…1;最小值表示为 1.00…0。尾数的表示范围为−1≤M≤−(1/2+2 −n)。
# 小结