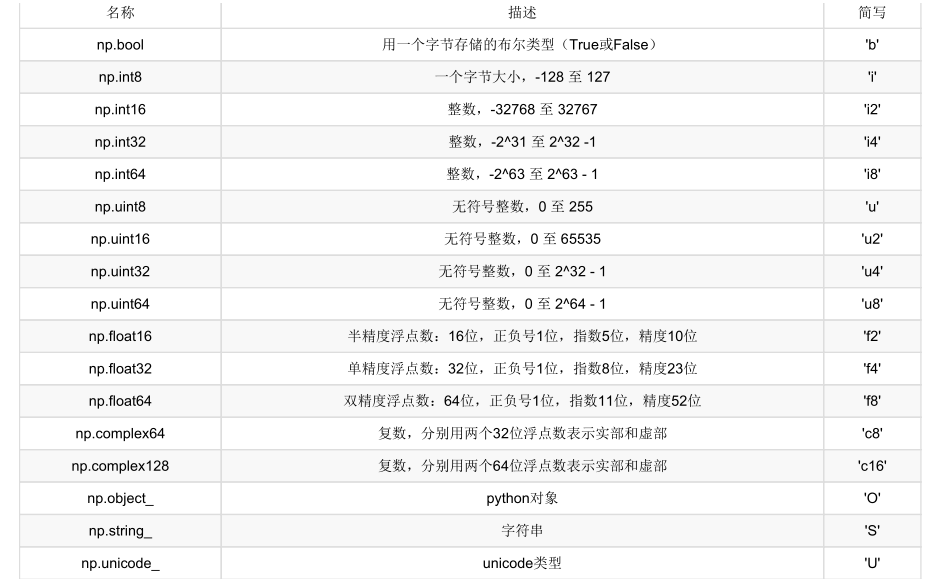
Numpy

开源的 python 科学计算库 用于快速处理任意维度的数组 npmpy 中存储对象是 ndarray

优势:

1. 内容块风格
2. 支持并行化运算
3. 效率高于纯 python
4. 底层使用了 C, 内部释放了 GIL

• np.array ([]) 创建 np 数组 返回 ndarray 对象

读取数据

np.genfromtxt("xxx.txt",delimiter=",",dtype=str) # 从txt中读取数据

数组转 ndarray

将数组或者多维数组转为 np 数组

np.arryay([5,10,15,1])
ndarray = np.arryay([[5,10,15,1],[15,2,5,3]])

• 列表中元素会自动转换为同一类 一般全部统一为一个类型
• 每个元素内 元素数必须相同

ndarray 数组方法

• ndarray.shape 数组维度和维度元素个数的元组
• ndarray.ndim 数组维数
• ndarray.size 数组中全部的元素数量
• ndarray.itemsize 一个数组元素的长度 (字节)
• ndarray.floor () 将数组中元素向上取整
• ndarray.dtype 数组元素的类型
  • 

ndarray 数组生成方法

• np.arange (15,30,5) 创建等差数组 生成一个 np 数组从 15 到 30 步进为 5 个 默认为 1 维
• p.logspace (start,stop, num) 创建等比数列 默认生成 50 个 num p.logspace (0,2, 3) 从 10 的 0 次方到 10 的 2 次方 生成 3 个元素 默认为 50 个
• np.zeros ((3,4)) 生成一个全为 0 的 np 数组 3 行 4 列
• np.zeros_like (a, dtype) 复制当前数组的维度和行列数 生成一个全为 0 的数组
• np.ones ((2,3,4), dtype=np.int32) 生成全为一的数组 二维三行 4 列 默认为 float64 类型 zeros 也是
• np.ones_like (a, dtype) 复制当前数组的维度和行列数 生成一个全为 1 的数组
• np.random.random ((2,3)) 多少个 random 就是多维 生成一个两行三列的数组 取值为 (-1,1)
• np.linspace (0,5,100) 生成一个 0-5 之间平均取 100 个值

数组的索引和切片

• ndarray [s,r] 根据维度和索引 获取值
• ndarray [0:] 支持切片

形状修改

• ndarray.reshape (shape, order) 将原数组 转为为指定的行列

  • stock_change = np.random.normal(0, 1, (8, 10))
    stock_change.reshape([10,8])  #将行列互换了  reshape方法并不会修改元素的个数和产生新的元素
    stock_change.reshape([-1,2])  #如果不知道具体的行或列可以使用-1代替 自动计算   如这里的 不知道多少行 每个行2个数据
    #一定要整除 否则报错
    

• ndarray.resize (new_shape) reshape 并不会对原数组进行修改 而产生新数组 我们使用 resize 可以对原数组进行修改

• ndarray.revel () 将数组变成一维 将全部元素存放为数组中

• ndarray.T 将数组的行、列进行互换

数组拼接

• np.hstack ((a,b)) 将两数组相连接
• np.vstack ((a,b)) 将两数组纵向拼接

数组切分

• np.hshplit (a,3) 将指定数组平均拆分成 3 个 np 数组 行的拆分 列数不变
• np.hshplit (a,(3,4)) 如果传递元组则在指定索引下 拆分 在第 3 列拆分 1 个 在第 4 列拆分 1 个 其他拆分为 1 个
• np.vshplit (a,3) 列拆分 行不变
• np.hshplit (a,(3,4)) 在指定列数拆分

类型修改

• ndarray.astype (flaot) 转换元素类型

  • df['金牌数'] = df['金牌数'].fillna("0").astype(int) #先替换缺失值
    

• ndarray.tostring ([order]) 转为字符串输出

• ndarray.tobytes ([order]) 转为字节数组

复制

• np.array (object, dtype) 将数组转为 np 数组 深拷贝
• np.asarray (a, dtype) 浅拷贝
• ndarray.copy () 浅拷贝
• ndarray.view () 深拷贝

数组的去重

• np.unique (nparray) 去重

数组运算

• np 数组支持两个 np 数组 之间运算 同时支持与常数运算

  • a = np.array([20,30,40,50])
    b = np.array([1,2,3])
    #数组在进行矢量化运算时，要求数组的形状是相等的。当形状不相等的数组执行算术运算的时候，就会出现广播机制，该机制会对数组进行扩展，使数组的shape属性值一样，这样，就可以进行矢量化运算了。
    a + b # [21,32,43,50]
    a - 1 # [19,29,39,49]
    a * 2 # [40,60,80,100]
    

• ndarray == 10 支持 > = < 比较运算符 返回为同样维度的布尔数组

  • na = np.arryay([5,10,15,1])
    t = na == 10
    print (na[t])  #因为返回是布尔数组 所以可以根据索引获取具体值
    print (na[na == 10])
    

• 支持 逻辑运算

  • na = np.arryay([5,10,15,1])
    t = (na >= 10) && (na <= 5)
    

• np.exp () 平方

• np.sqrt () 开根号

• np.tile (a,(2,2)) 将行数和列数扩展为指定倍数 传递数组和一个元组

判断函数

• np.all () 所有元素都符合条件则返回 true np.all (arry>60 )
• np.any () 有一个符合则返回 true
• np.where (temp> 60, 1, 0) 三元运算符 成立返回参数 2 否则返回参数 3
• ndarray.argmax (axis=) 返回最大值的索引

排序

• ndarray.sort (axis=) 排序默认为升序
• ndarray.argsort (axis=) 按元素排序 返回元素之前的索引

统计运算

• ndarray.min (axis) 获取最小值

• ndarray.max (axis) 获取最大值

• ndarray.sum (axis=1) 求和 axis=1 则为行求和 axis=0 为列切换

• ndarray.median (axis) 返回中位值

• ndarray.mean (axis,dtype) 返回平均值

• ndarray.std (axis,dtype) 返回标准差

• ndarray.var (axis,dtype) 返回方差

正态分布

正态分布是一种概率分布。正态分布是具有两个参数 μ 和 σ 的连续型随机变量的分布，第一参数 μ 是服从正态分布的随机变量的均值，第二个参 数 σ 是此随机变量的标准差，所以正态分布记作 N (μ，σ)。

矩阵

矩阵必须是二维的 但 array 可以是多维的

$$A=\left\{\begin{array}{ccccc}a& b& c& d& e\\ f& g& h& i& j\\ k& l& m& n& o\\ p& q& r& s& t\end{array}\right\}$$

向量

向量是一种特殊的矩阵 向量一般都是列向量

如: (3x1) 的矩阵

向量是一维的

加法和标量乘法

• 加法：行列数相等时可以相加

• 乘法：标 (常) 量 乘以 矩阵 直接相乘 按原来位置

• 矩阵向量乘法: (M 行，N 列) X (N 行，L 列) = (M 行，L 列) 并且 N 列和 N 行相等

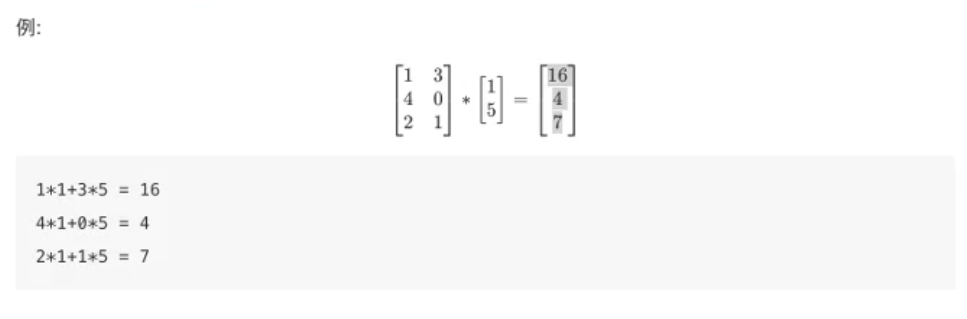
• 矩阵乘法:

即 A 的第一行 各个数 都乘以 B 的第一列各个数 相加 得到 C 的第一行第一个数

​ 第一行 各个数 都乘以 B 的第二列各个数 相加 得到 C 的第一行第二个数

矩阵乘法的性质

• 矩阵乘法不满足交换律 A*B != B*A
• 矩阵的乘法满足结合律: A*(B*C)=(A*B)*C
• 单位矩阵：在矩阵乘法中 有一种特殊矩阵 称为单位矩阵 它是个方针 一般用 I 或者 E 表示 从左上角到右下角的对角线 (称为主对角线) 上的元素均为为 1 其他全为 0 如果 A*B=E 那么矩阵 A 和 B 互为逆矩阵

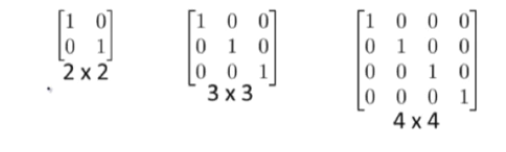
逆、转置

1. 待定系数法

给予一个 2X2 的矩阵 我们假设一个同样为 2X2 的矩阵 [a b] [b c]

A B 矩阵相乘 转为单位矩阵

求出 a b c d 的值，就可以得出 A 的逆矩阵

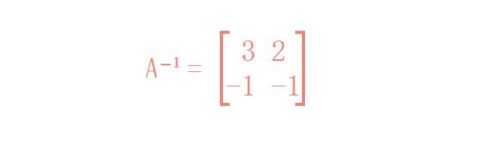
2. 伴随矩阵求逆矩阵

• 伴随矩阵是矩阵元素所对应的代数余子式，所构成的矩阵，转置后得到的新矩阵。

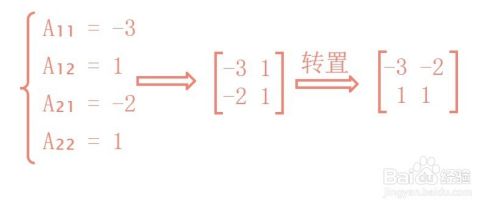
原矩阵为 [1 2]

​ [-1 -3]

A11 为 第一行和第一列的元素 都去掉剩下 -3 又因为 A11 为 1+1=2 为偶数是整数 1*-3=-3 A11=-3

A12 为 第一行和第二列的元素 都去掉剩下 -1 又因为 A12 为 1+2=3 为奇数 所以为负号 A12=-(-1)=1

A21 为 第二行和第一列的元素 都去掉剩下 2 2+1 为奇数 A21=-(2)=-2

A22 为 第二行和第二列的元素 都去掉剩下 1 为偶数 A22=1

得出 [-3 1] 的矩阵 进行转置即行列变换第一行内容变成第一列内容 变成 [-3 -2]

​ [-2 1] 第二行内容变成第二列内容 [1 1]

接下来求出矩阵 A 的行列式

• 行列式

二阶行列式的计算方法是 “对角线法则” 主对角线元素积与副对角线元素积的差

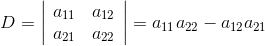
二阶行列式并不适合三阶使用

正对角线为正，反对角线为负。

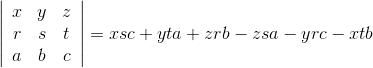
xsc + yt*a + ra* z - zsa - yr*c - tb* x

由行列号性质得出

|A|1*(-1)-(-1)*2=-1

A⁻¹=A*/|A| = A*/(-1)=-A* = [3 2]

​ [-1 -1]

3. 初等变换求逆矩阵

首先我们得出 A 的增广矩阵

然后进行初等行变换。依次进行

第 1 行加到第 2 行，得到

第 2 行 ×2 加到第 1 行，得到

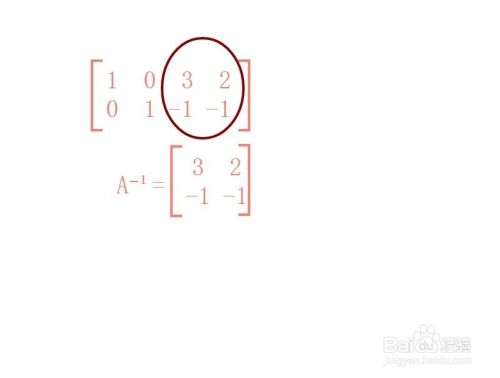
第 2 行 ×(-1)，得到

因此逆矩阵 A⁻¹=

3 2

-1 -1

转置

即将矩阵的行列互换

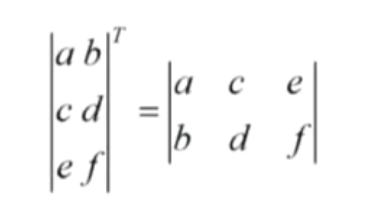
np 方法

• np.matmul()

  • a = np.array([[80, 86], [82, 80], [85, 78], [90, 90],
                 [86, 82], [82, 90]])  # 是的多行2列的矩阵
    b = np.array([[0.7], [0.3]])  # 两行一列的矩阵
    np.matmul(a, b)  # 转为M行L列 即多行一列
    

• np.dot()

  • #np.matmul(a, 10) #只支持矩阵相乘
    np.dot(a, 10)  # matmul和dot功能一致 但dot支持点乘  标量运算 matmul不支持点乘