前缀和数组

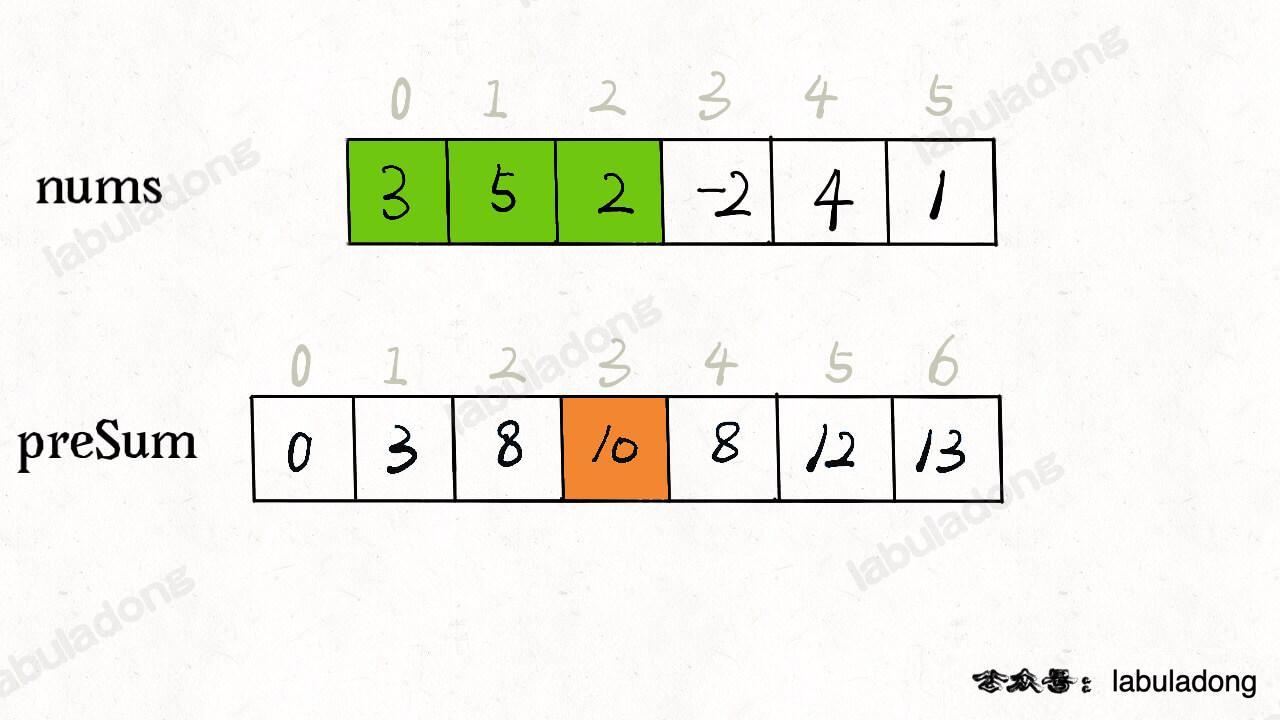
假设我们需要求指定数组中 l ~ r 范围元素的和

方法一：我们使用一个二维数组存储所有 l-r 的元素和的结果 (需要 n*n/2 的空间)

方法二：使用前缀和数组 求出 每个元素 0~ 元素本身的和 (需要 n 的空间存储结果)

当我们求 3 ~ 7 范围的和 我们返回 ans [7] 即 0~7 的结果 减去 ans [2] 即 0~2 的结果 即可以快速取得指定范围内的合

sum[i···j] = arr[0···j] - arr[0···i-1]

此方法我们称为 前缀和数组

class NumArray {
    // 前缀和数组
    private int[] preSum;

    /* 输入一个数组，构造前缀和 */
    public NumArray(int[] nums) {
        // preSum[0] = 0，便于计算累加和
        preSum = new int[nums.length + 1];
        // 计算 nums 的累加和
        for (int i = 1; i < preSum.length; i++) {
            preSum[i] = preSum[i - 1] + nums[i - 1];
        }
    }
    
    /* 查询闭区间 [left, right] 的累加和 */
    public int sumRange(int left, int right) {
        return preSum[right + 1] - preSum[left];
    }
}

差分数组

差分数组的主要适用场景是频繁对原始数组的某个区间的元素进行增减

比如说，我给你输入一个数组 nums ，然后又要求给区间 nums[2..6] 全部加 1，再给 nums[3..9] 全部减 3，再给 nums[0..4] 全部加 2，再给…

这里就需要差分数组的技巧，类似前缀和技巧构造的 prefix 数组，我们先对 nums 数组构造一个 diff 差分数组，diff[i] 就是 nums[i] 和 nums[i-1] 之差：

int[] diff = new int[nums.length];
// 构造差分数组
diff[0] = nums[0];
for (int i = 1; i < nums.length; i++) {
    diff[i] = nums[i] - nums[i - 1];
}

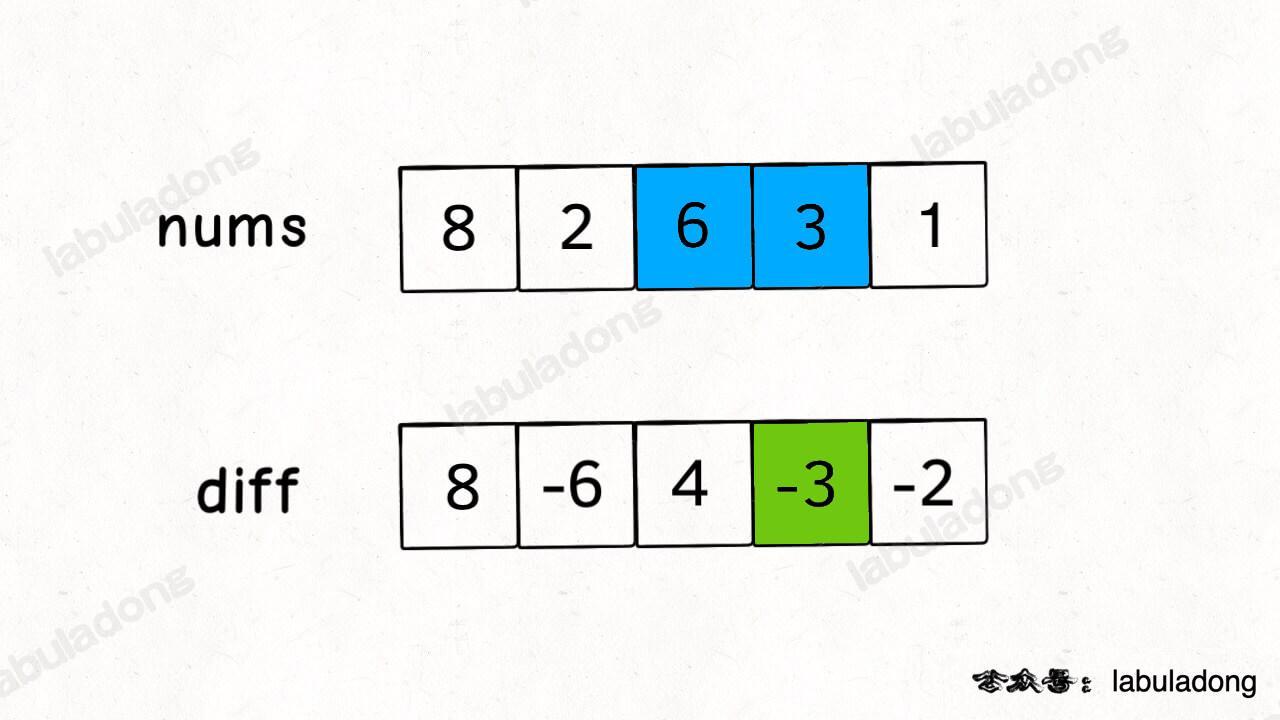
通过这个 diff 差分数组是可以反推出原始数组 nums 的，代码逻辑如下：

int[] res = new int[diff.length];
// 根据差分数组构造结果数组
res[0] = diff[0];
for (int i = 1; i < diff.length; i++) {
    res[i] = res[i - 1] + diff[i];
}

这样构造差分数组 diff ，就可以快速进行区间增减的操作，如果你想对区间 nums[i..j] 的元素全部加 3，那么只需要让 diff[i] += 3 ，然后再让 diff[j+1] -= 3 即可：

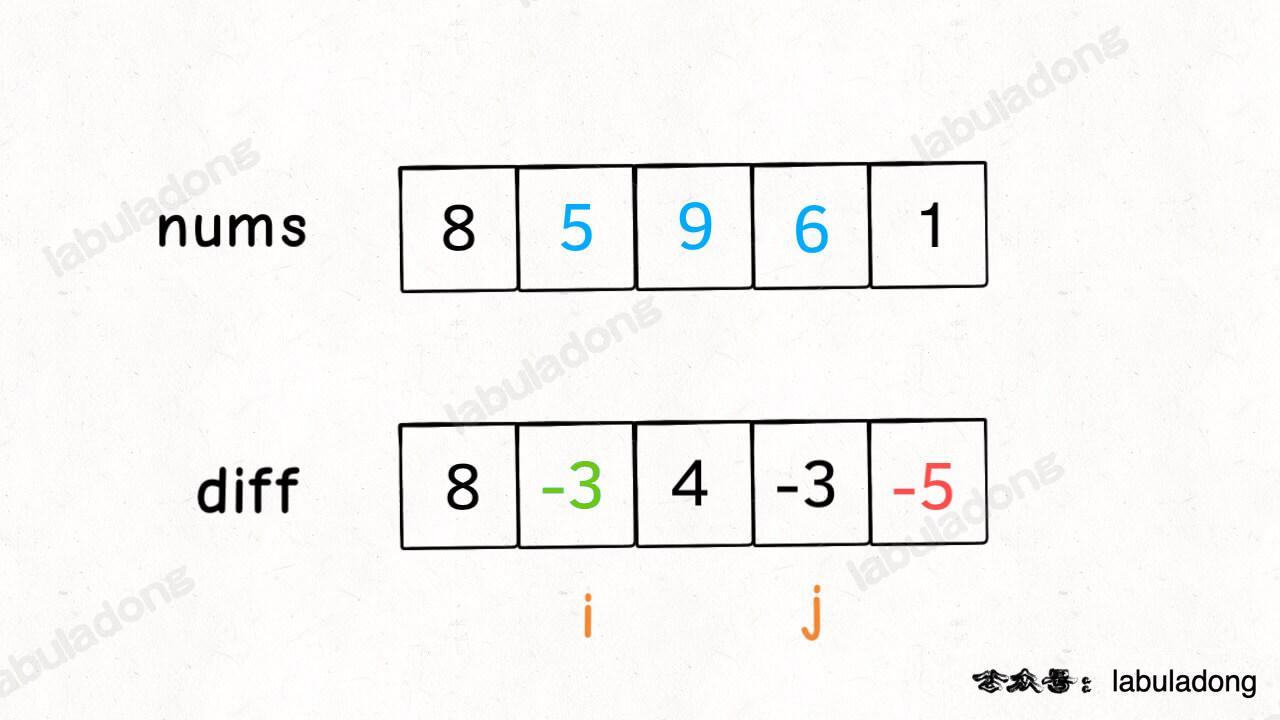
原理很简单，回想 diff 数组反推 nums 数组的过程， diff[i] += 3 意味着给 nums[i..] 所有的元素都加了 3，然后 diff[j+1] -= 3 又意味着对于 nums[j+1..] 所有元素再减 3，那综合起来，是不是就是对 nums[i..j] 中的所有元素都加 3 了

只要花费 O (1) 的时间修改 diff 数组，就相当于给 nums 的整个区间做了修改。多次修改 diff ，然后通过 diff 数组反推，即可得到 nums 修改后的结果。

// 差分数组工具类
class Difference {
    // 差分数组
    private int[] diff;
    
    /* 输入一个初始数组，区间操作将在这个数组上进行 */
    public Difference(int[] nums) {
        assert nums.length > 0;
        diff = new int[nums.length];
        // 根据初始数组构造差分数组
        diff[0] = nums[0];
        for (int i = 1; i < nums.length; i++) {
            diff[i] = nums[i] - nums[i - 1];
        }
    }

    /* 给闭区间 [i, j] 增加 val（可以是负数）*/
    public void increment(int i, int j, int val) {
        diff[i] += val;
        ///注意边界问题
        if (j + 1 < diff.length) {
            diff[j + 1] -= val;
        }
    }

    /* 返回结果数组 */
    public int[] result() {
        int[] res = new int[diff.length];
        // 根据差分数组构造结果数组
        res[0] = diff[0];
        for (int i = 1; i < diff.length; i++) {
            res[i] = res[i - 1] + diff[i];
        }
        return res;
    }
}