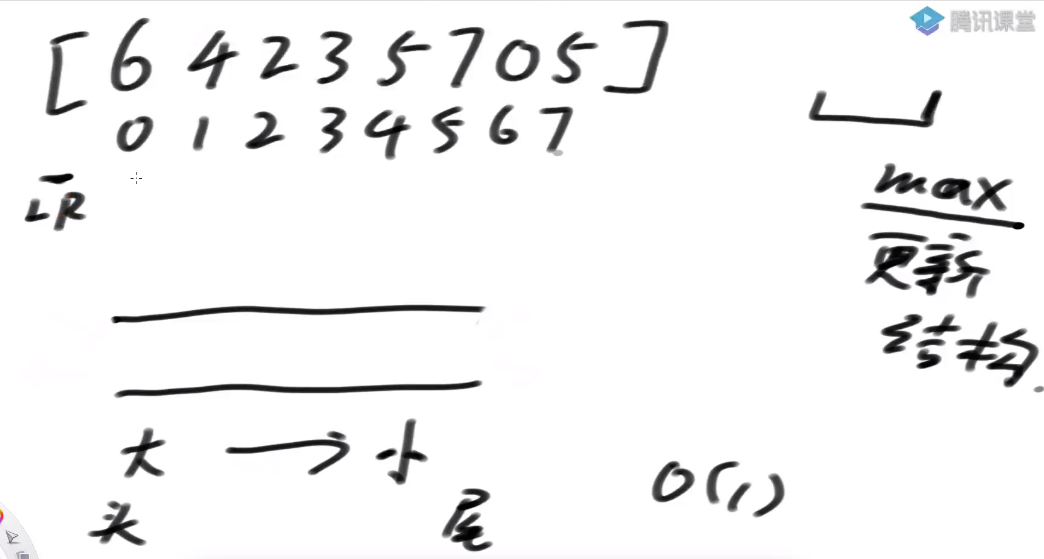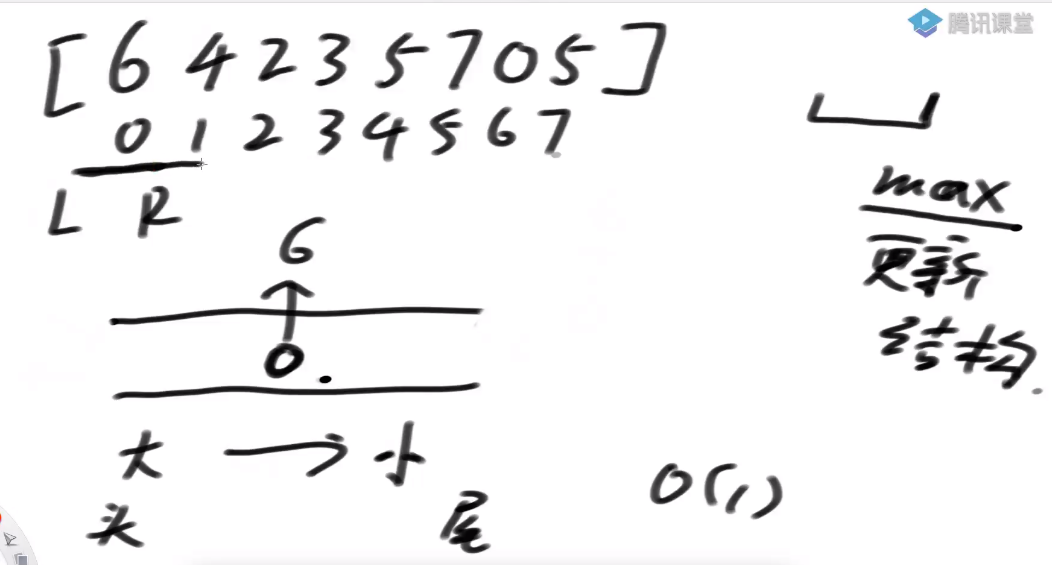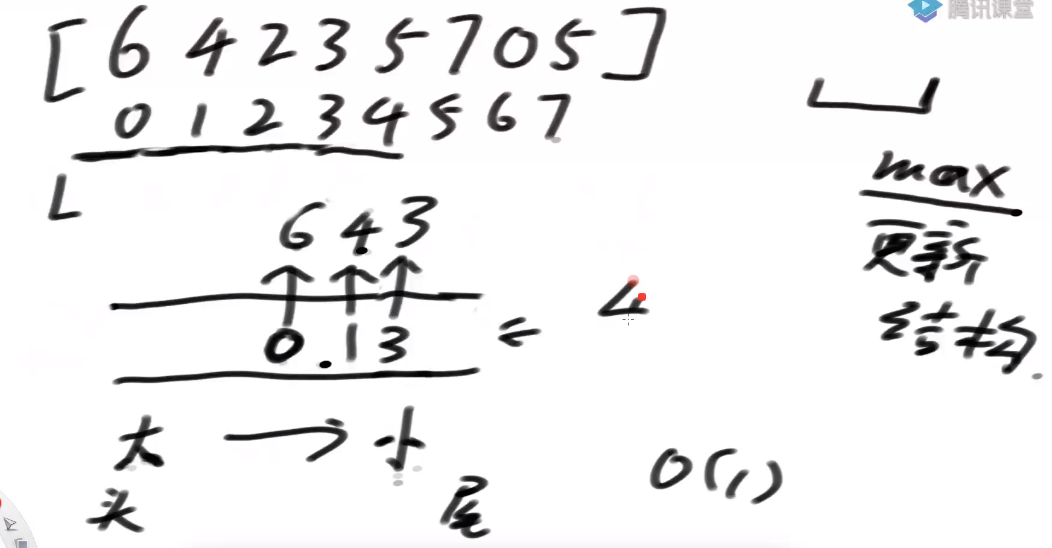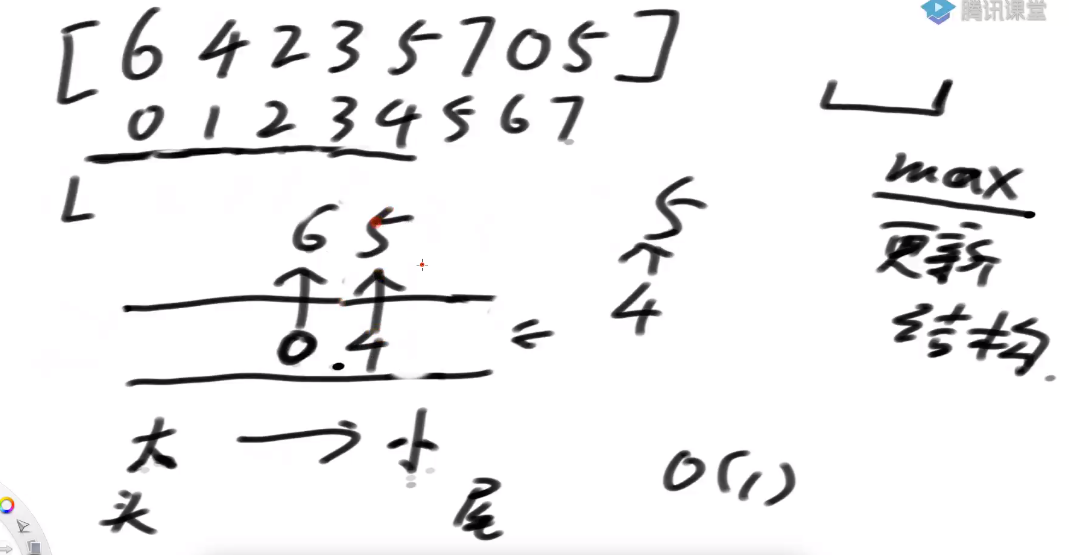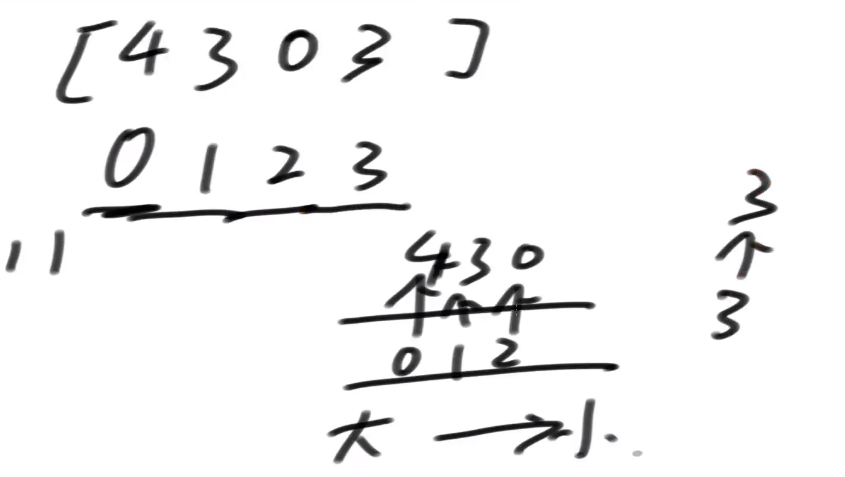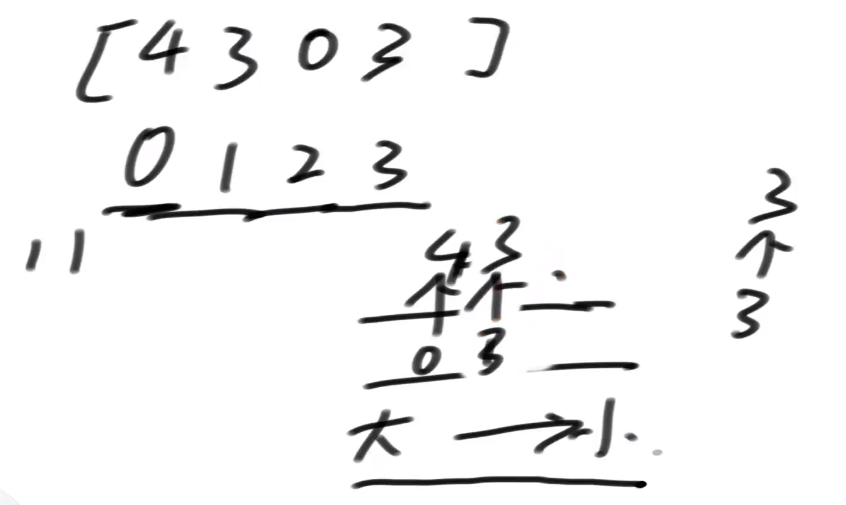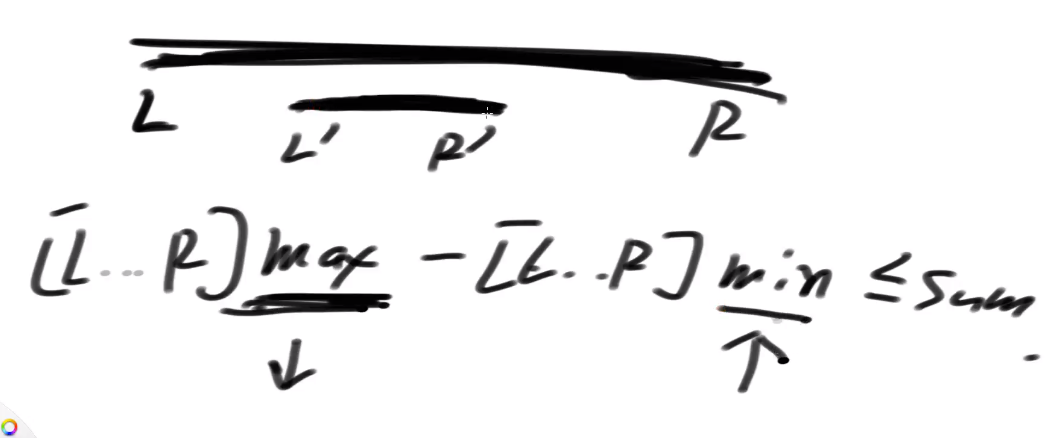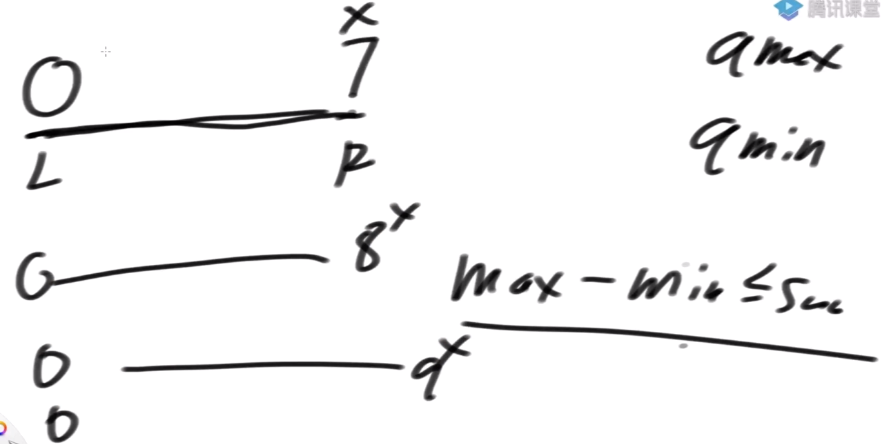滑动窗口
滑动窗口
# 滑动窗口
认为规定好的一些运动轨迹 一开始左边界,右边界在数组的左侧,没有包住任何数 规定:
- 可以在任何时刻,让 R++, R 往右动,意味着一个数会从窗口的右侧进入窗口 除非到了终止位置,R 不要再往右了
- 可以在任何时刻,让 L++, L 往右动,意味着某一个数会从窗口的左侧出窗口
遵循一个原则: 左边界不要跑到右边界的再右侧去
可以动态的让窗口动态的从右侧进去,从左侧出去
我在每一个时刻都会维持一个窗口,想知道在一个窗口形成的状况下,窗口内的最大值是多少? 怎么得到窗口内的最大值 每次形成窗口的确可以遍历得到最大值,但是复杂度比较高 有没有非常好的办法,迅速的得到最大值?
双端队列
准备好一双端的队列 任何一个状态下,窗口内最大值的更新结构 准备一个数组 [6,4,2,3,5,7,0,5] 准备好一个双堆队列:可以在头部尾部进出,O (1)
最大值的更新结构: 从头部到尾部,从大到小
当 R 右移,一个数字进窗口 L..R 包住了 6 这个数,从尾部加入双端队列,双端队列是空的,6 直接进去
双端队列头部所代表的值就是此时最大值
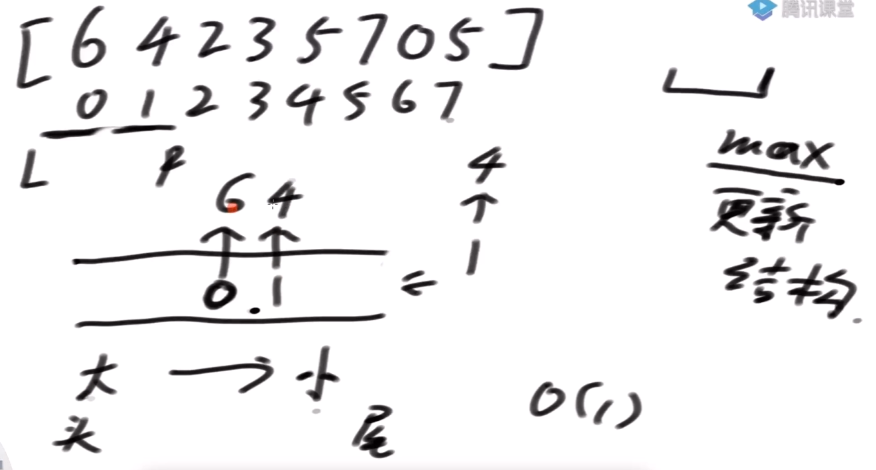
R++,4 进入窗口,从尾部进入
从头部到尾部由大到小,4 在后面,没有改变由大到小这个事实
继续 R++ 直到来到 3 的位置 改变了由大到小的事实,不能直接进,怎么办? 从尾部弹出,2 位置的 2 弹出,扔出去的数再也不找回了 3 位置的 3 落到 4 后面
如有重复值 不保留旧的 只保留最新的
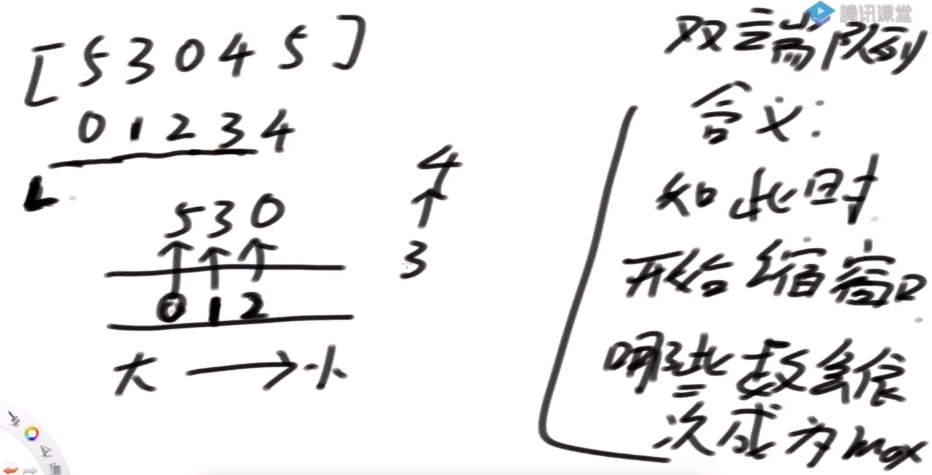
双端队列的根本含义 假设此时我如果让窗口依次缩小的话,哪些位置的数会依次成为窗口内的最大值
窗口的此时的最大值是 5
使 L 指针 ++ 缩窗口,轮到 1 位置的 3 成为最大值 增加窗口 2 位置的 0 过来 0 位置的 5, 1 位置的 3, 2 位置的 0 依次成为最大值
想让 L 往右,双端队列怎么更新 看头部的下标有没有过期 双端队列头部下标的数值就是窗口内的最大值
所以如果你 L 位置跟 R 位置会划过整数组中,所有的数 每一个位置的数,最多进一次,出一次 更新总代价 O (N), 查询很快 O (1), 均摊下来每一个数代价 O (1)
# 滑动窗口最大值
窗口内最大值或最小值更新结构的实现
假设一个固定大小为W的窗口,依次划过arr,
返回每一次滑出状况的最大值
例如,arr = [4,3,5,4,3,3,6,7], W = 3
返回:[5,5,5,4,6,7]
2
3
4
5
# 暴力枚举
// 暴力方法
public static int[] right(int[] arr, int w) {
if (arr == null || w < 1 || arr.length < w) {
return null;
}
int n = arr.length;
int[] res = new int[n - w + 1];
int index = 0;
// 左指针
int l = 0;
// 右指针
int r = w - 1;
while (r < n) {
int max = arr[l];
// 左指针移动w个 求区间最大值
for (int i = l + 1; i <= r; i++) {
max = Math.max(max, arr[i]);
}
// 保存区间最大值结果
res[index++] = max;
// 左右指针滑动
l++;
r++;
}
return res;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# 滑动窗口
public static int[] getMaxWindow(int[] arr,int w) {
if (arr == null || w < 1 || arr.length < w) {
return null;
}
//双端队列
LinkedList<Integer> queue = new LinkedList<>();
int[] res = new int[arr.length-w+1];
int index = 0;
for (int r = 0; r < arr.length; r++) {
//队列不为空 并且当前队列未的数值 小于或等于 arr[r]
while (!queue.isEmpty() && arr[queue.peekLast()] <= arr[r]) {
//移除队列
queue.pollLast();
}
//队列存储的为下标
queue.add(r);
//查看当前队头最大值的下标 是否超出当前窗口的范围内
if (queue.peekFirst() == r -w) {
//超出当前窗口范围 移除当前队列最大值
queue.pollFirst();
}
//当前窗口已经形成 记录每个窗口的最大值
if(r >= w-1) {
res[index++] = arr[queue.peekFirst()];
}
}
return res;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# 达标子数组
给定一个整型数组arr,和一个整数num
某个arr中的子数组sub,如果想达标,必须满足:sub中最大值 – sub中最小值 <= num,
返回arr中达标子数组的数量
2
3
# 暴力枚举
// 暴力解法
public static int right(int[] arr, int sum) {
if (arr == null || arr.length == 0 || sum < 0) {
return 0;
}
int n = arr.length;
int count = 0;
for (int l = 0; l < n; l++) {
for (int r = l; r < n; r++) {
int max = arr[l];
int min = arr[l];
// 从l..r窗口范围内遍历查找 最小值和最大值
for (int i = l + 1; i <= r; i++) {
max = Math.max(max, arr[i]);
min = Math.min(min, arr[i]);
}
// 最大最小值 <= sum 则 count++
if (max - min <= sum) {
count++;
}
}
}
return count;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# 滑动窗口
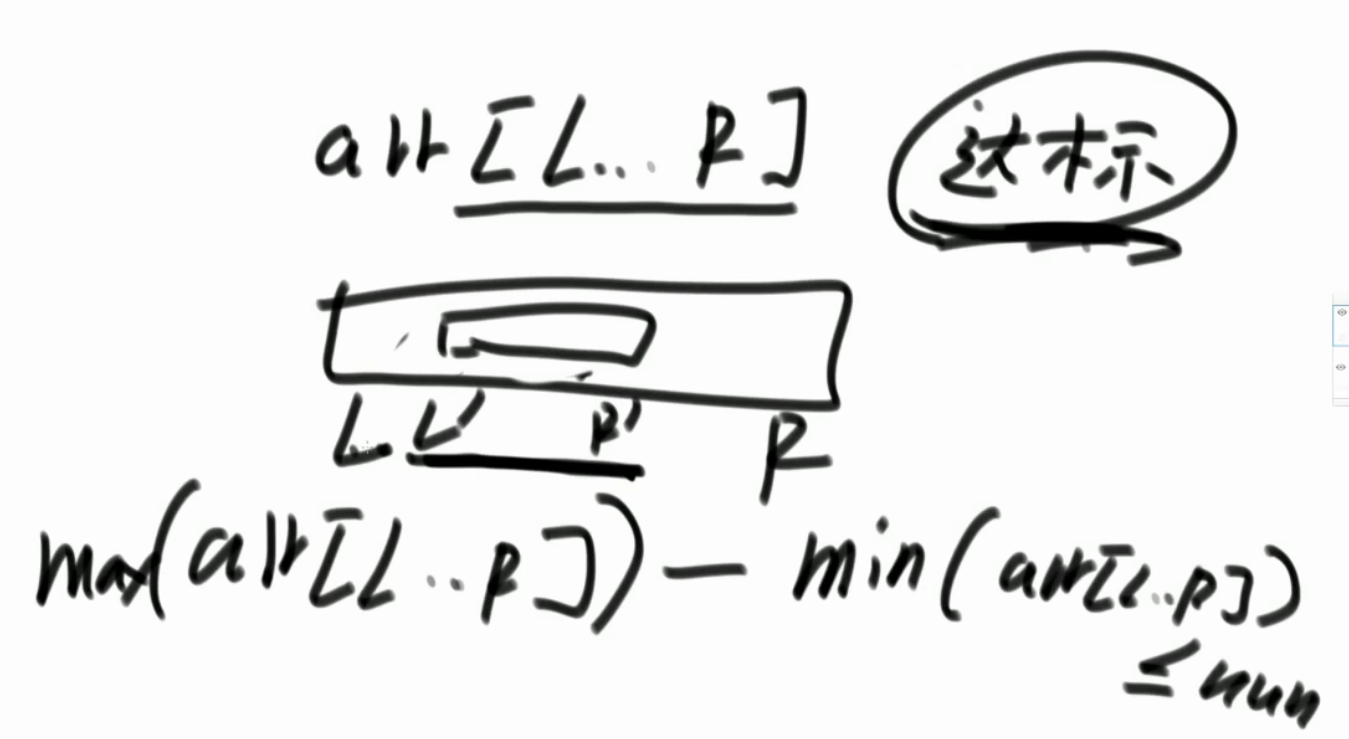
假设某一个子数组从 L ... R 范围已经达标,则内部所有子数组一定也都达标
小范围的最大,最小值:最大值变小,最小值变大,所以一定达标
子数组 最大值变小,最小值变大,一定都达标
如果 L..R 不达标,则 L 往左扩,R 往右扩出来的新的子数组一定也都不达标 范围扩大,更加悬殊
准备窗口内最大值的更新结构 qmax 和最小值的两个更新结构 qmin 假设窗口从 0 开始 如果达标,窗口就继续扩展 扩到一旦不达标,停止扩展
一个范围 L...R 如果达标, 它内部所有子数组都达标 如果 L 到 R 已经不达标, R 再往右扩, 都不达标 让零开始看看扩到什么时候是初次不达标的时候
缩窗口,L 来到 1 位置,看 R 能不能往右扩 必须以 1 位置开头的字数组达标数量是多少个?整个过程中,整体代价 O (N) L,R 位置都不回退,窗口内两个最大值, 最小值更新结构,一共只不过 N 个数
public static int num(int[] arr, int sum) {
if (arr == null || arr.length == 0 || sum < 0) {
return 0;
}
int n = arr.length;
int count = 0;
LinkedList<Integer> maxWindow = new LinkedList<>();
LinkedList<Integer> minWindow = new LinkedList<>();
int r = 0;
for (int l = 0; l < n; l++) {
while (r < n) {
//max队列不为空 并且当前队列尾元素 小于或等于 arr[r]
while (!maxWindow.isEmpty() && arr[maxWindow.peekLast()] <= arr[r]) {
maxWindow.pollLast();
}
//加入当前下标
maxWindow.addLast(r);
//min队列不为空 并且当前队列尾元素 大于或等于 arr[r]
while (!minWindow.isEmpty() && arr[minWindow.peekLast()] >= arr[r]) {
minWindow.pollLast();
}
//加入当前下标
minWindow.addLast(r);
if(arr[maxWindow.peekFirst()] - arr[minWindow.peekFirst()] > sum) {
//当前窗口最大最小值之差 大于sum 直接结束当前窗口的r指针增加
break;
} else {
//否则r++ 继续扩大窗口大小
r++;
}
}
//当前窗口 一共有 r-l个达标子数组
count += r- l;
//接下来l要进行滑动
//查看max窗口的最大值是否是l 如是l直接移除
if(maxWindow.peekFirst() ==l) {
maxWindow.pollFirst();
}
if(minWindow.peekFirst() == l) {
minWindow.pollFirst();
}
}
return count;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
# 加油站问题
加油站的良好出发点问题
N个加油站组成一个环形,给定两个长度都是N的非负数组 gas和cost(N>1),gas[i]代表 第i个加油站存的油可以跑多少千米,cost[i]代表第i个加油站到环中下一个加油站相隔 多少千米。 假设你有一辆油箱足够大的车,初始时车里没有油。如果车从第i个加油站出发,最终 可以回到这个加油站,那么第i个加油站就算良好出发点,否则就不算。 请返回长度为N的boolean型数组res,res[i]代表第 i 个加油站是不是良好出发点。
2
# 最少货币问题
动态规划中利用窗口内最大值或最小值更新结构做优化(难)
arr是货币数组,其中的值都是正数。再给定一个正数aim。
每个值都认为是一张货币,
返回组成aim的最少货币数
注意:因为是求最少货币数,所以每一张货币认为是相同或者不同就不重要了
2
3
4
5