线性表

线性表定义、基本操作

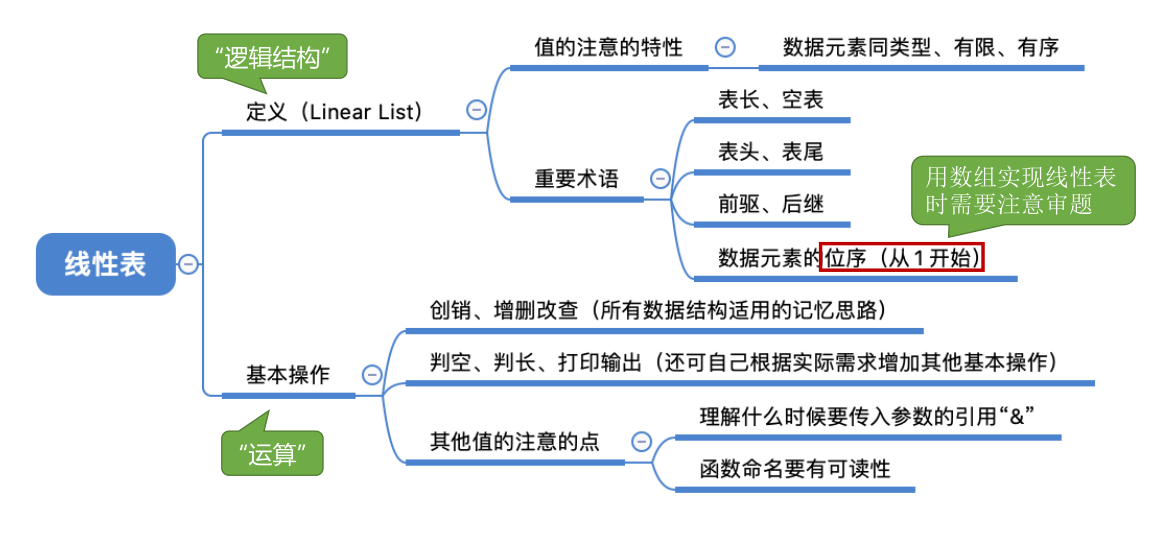
数据结构三要素 —— 逻辑结构、数据的运算、 存储结构（物理结构）

线性表的定义

线性表是具有相同数据类型的$n（n\ge 0）$个数据元素的有限序列，其中$n$ 为表长，当$n=0$ 时线性表是一个空表。若用$L$ 命名线性表，则其一般表示为

$L=(a_1,a_2,\dots ,a_i,a_{i+1},\dots ,a_n)$

上述有几个概念：

• $a_i$ 是线性表中的 第i个 元素线性表中的位序。注意：位序是从 1 开始的
• $a_1$ 是表头元素；$a_n$ 是表尾元素。
• 除第一个元素外，每个元素有且仅有一个直接前驱；除最后一个元素外，每个元素有且仅有一个直接后继。

基本操作

• InitList(&L) ：初始化表。构造一个空的线性表 L，分配内存空间。
• DestroyList(&L) ：销毁操作。销毁线性表，并释放线性表 L 所占用的内存空间。
• ListInsert(&L,i,e) ：插入操作。在表 L 中的第 i 个位置上插入指定元素 e。
• ListDelete(&L,i,&e) ：删除操作。删除表 L 中第 i 个位置的元素，并用 e 返回删除元素的值。
• LocateElem(L,e) ：按值查找操作。在表 L 中查找具有给定关键字值的元素。
• GetElem(L,i) ：按位查找操作。获取表 L 中第 i 个位置的元素的值。

其他常用操作：

• Length(L) ：求表长。返回线性表 L 的长度，即 L 中数据元素的个数。
• PrintList(L) ：输出操作。按前后顺序输出线性表 L 的所有元素值。
• Empty(L) ：判空操作。若 L 为空表，则返回 true，否则返回 false。

关于定义操作的五个小提示：

1. 对数据的操作（记忆思路） —— 创销、增删改查

2. C 语言函数的定义 —— <返回值类型> 函数名 (< 参数 1 类型 > 参数 1，< 参数 2 类型 > 参数 2，……)

3. 实际开发中，可根据实际需求定义其他的基本操作

4. 函数名和参数的形式、命名都可改变（Reference：严蔚敏版《数据结构》）

5. 什么时候要传入引用 & —— 对参数的修改结果需要 “带回来”，只有 C++ 才支持这种写法。 对于参数的修改只是局部的修改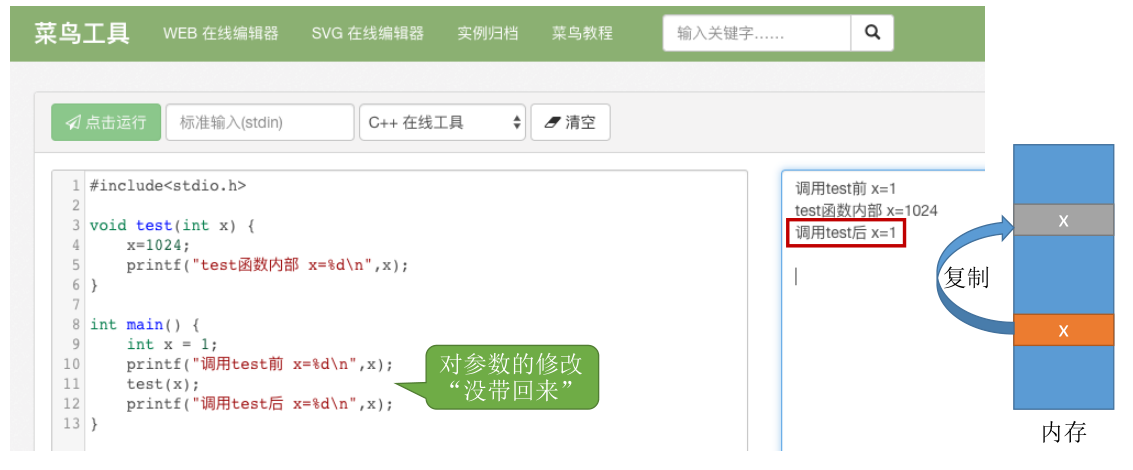

   对于参数的修改是全局的即需要带回来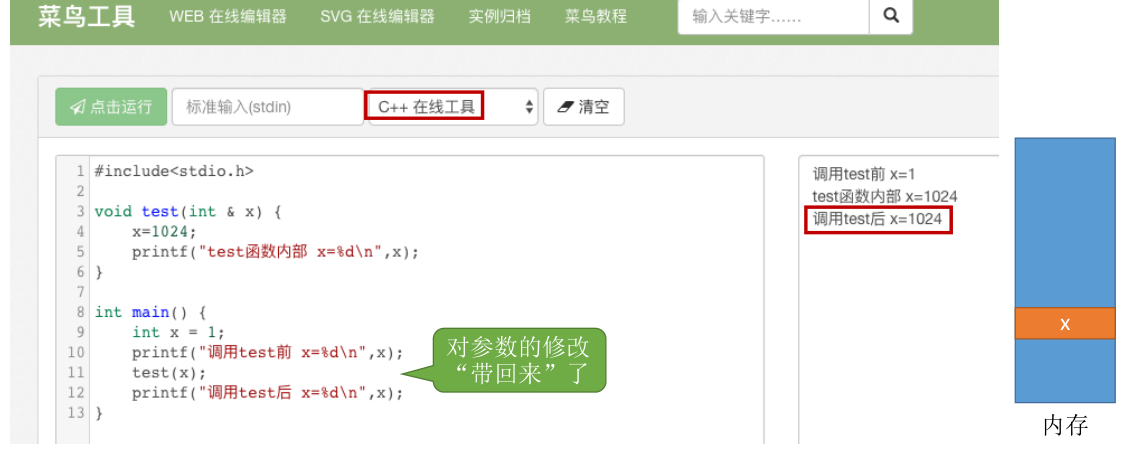

为什么要实现对数据结构的基本操作？

1. 团队合作编程，你定义的数据结构要让别人能够很方便的使用（封装）
2. 将常用的操作 / 运算封装成函数，避免重复工作，降低出错风险

比起学会 “How”，更重要的是想明白 “Why”

总结

顺序表

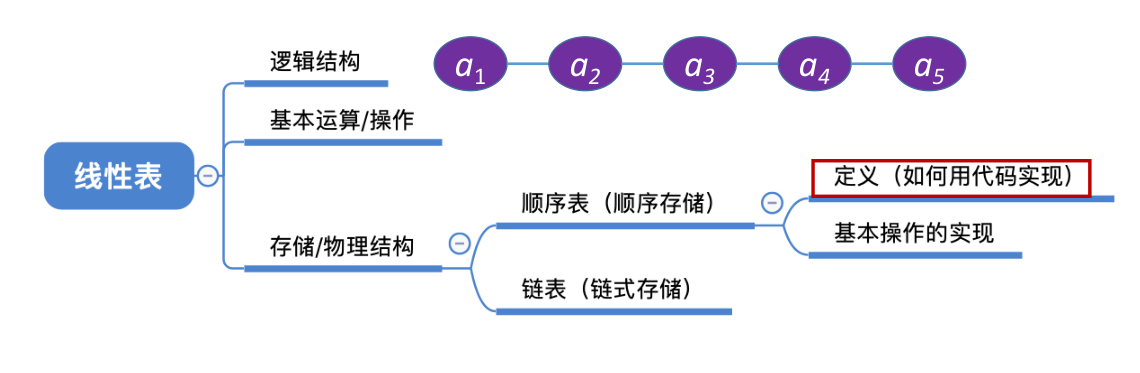
顺序表的定义

顺序表――用顺序存储的方式实现线性表

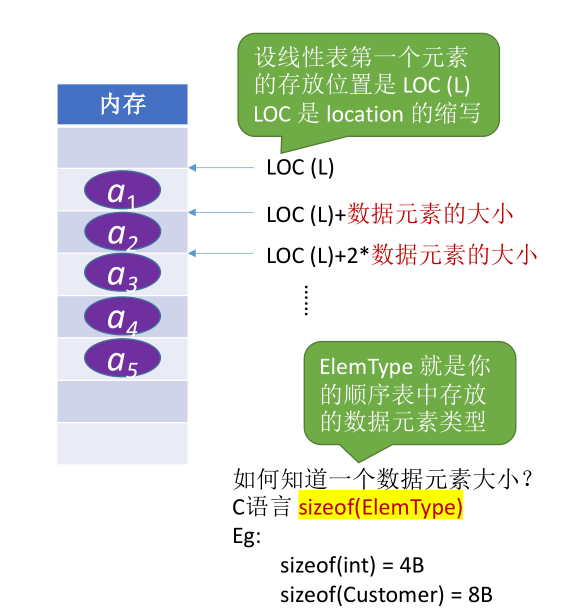
顺序表的实现

静态分配

#define MaxSize 10 //定义最大长度
typedef struct{
    ElemType data[MaxSize]; //用静态的“数组”存放数据元素
    int length; //顺序表的当前长度
}SqList; //顺序表的类型定义（静态分配方式）

动态分配

#define InitSize 10 //顺序表的初始长度
typedef struct{
    ElemType *data; //指示动态分配数组的指针
    int MaxSize; //顺序表的最大容量
    int length; //顺序表的当前长度
} SeqList; //顺序表的类型定义（动态分配方式）

动态申请和释放内存空间：

C 语言使用 malloc、free 函数

// malloc 函数返回一个指针，需要强制转型为你定义的数据元素类型指针
L.data = (ElemType *) malloc (sizeof(ElemType) * InitSize); // malloc 函数的参数，指明要分配多大的连续内存空间

malloc 申请存储空间

而在 C++ 是使用 new、delete 关键字

---

#define InitSize 10 //顺序表的初始长度
typedef struct{
    int *data; //指示动态分配数组的指针
    int MaxSize; //顺序表的最大容量
    int length; //顺序表的当前长度
} SeqList; 

// 初始化顺序表
void InitList(SeqList &L){
    //用 malloc 函数申请一片连续的存储空间
    L.data=(int *)malloc(InitSize*sizeof(int));
    L.length=0;
    L.MaxSize=InitSize;
}

// 扩展顺序表
void IncreaseSize(SeqList &L,int len){
    int *p=L.data;
    // 开辟新的空间
    L.data=(int *)malloc((L.MaxSize+len)*sizeof(int));
    // 将数据复制到新区域 也可以使用 realloc 进行动态扩容
    for(int i=0; i<L.length; I++){
        L.data[i]=p[i];
    }
    L.MaxSize=L.MaxSize+len;
    free(p); //释放原来的内容空间
}

int main(){
    SeqList L;
    InitList(L);
    IncreaseSize(L,5);
    return 0;
}

顺序表的特点

顺序表的特点：

1. 随机访问 ，即可以在 $O(1)$ 时间内找到第 i 个元素。
2. 存储密度高，每个节点只存储数据元素
3. 拓展容量不方便（即便采用动态分配的方式实现，拓展长度的时间复杂度也比较高）
4. 插入、删除操作不方便，需要移动大量元素

总结

顺序表插入和删除

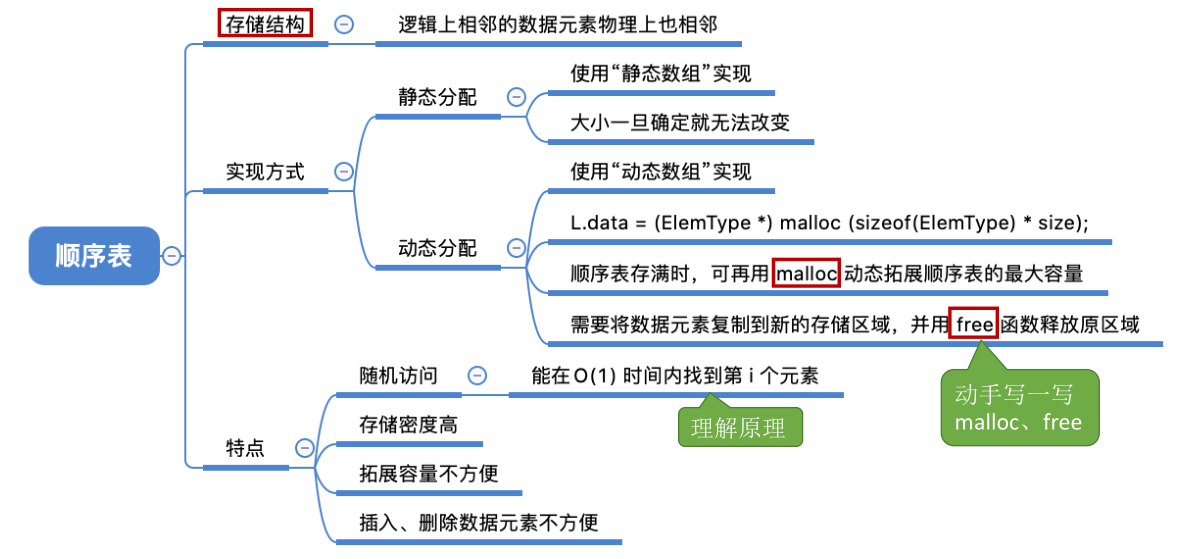
插入

• ListInsert(&L,i,e) ：插入操作。在表 L 中的第 i 个位置上插入指定元素 e。

#include <stdio.h>
#include <stdlib.h>

#define MaxSize 10 //定义最大长度
typedef struct {
	int data[MaxSize]; //用静态的“数组”存放数据元素
	int length; //顺序表的当前长度
} SqList; //顺序表的类型定义（静态分配方式）

// 插入操作
bool ListInsert(SqList &L, int i, int e) {
	// 判断i的范围是否有效
	if (i < 1 || i > L.length + 1) {
		return false;
	}
	//当前存储空间已满，不能插入
	if (L.length >= MaxSize) {
		return false;
	}
	// 将第i个元素及其之后的元素后移
	for (int j = L.length; j >= i; j--) {
		L.data[j] = L.data[j - 1];
	}
	// 在位置i处插入e
	L.data[i - 1] = e;
	// 顺序表长度+1
	L.length++;
	return true;
}

// 初始化顺序表
void InitList(SqList &L) {
	L.length = 0;
}

int main() {
	SqList L;
	InitList(L);
	ListInsert(L, 1, 66);
	ListInsert(L, 2, 77);
	printf("%d\n", L.data[1]);
	return 0;

}

关注最深层循环语句的执行次数与问题规模。即上述代码块中的第 22 行代码的执行次数。

• 最好情况：新元素插入到表尾，不需要移动元素

  i = n+1，循环 0 次；最好时间复杂度 = O (1)

• 最坏情况：新元素插入到表头，需要将原有的 n 个元素全都向后移动 i = 1，循环 n 次；最坏时间复杂度 = O (n);

• 平均情况：假设新元素插入到任何一个位置的概率相同，即 $i=1,2,3,\dots ,length+1$ 的概率都是 $p=\frac{1}{n+1}$ $i=1$，循环 $n$ 次；$i=2$ 时，循环 $n-1$ 次；$i=3$，循环 $n-2$ 次 …… $i=n+1$ 时，循环$0$ 次 平均循环次数 $=np+(n-1)p+(n-2)p+\dots \dots +1\cdot p=\frac{n(n+1)}{2}\frac{1}{n+1}=\frac{n}{2}\Rightarrow$ 平均时间复杂度 $ = O (n)$

删除

• ListDelete(&L,i,&e) ：删除操作。删除表 L 中第 i 个位置的元素，并用 e 返回删除元素的值。

// 删除操作
bool ListDelete(SqList &L, int i, int &e) {
	// 判断i的范围是否有效
	if (i < 1 || i > L.length) {
		return false;
	}
	// 将被删除的元素赋值给e
	e = L.data[i - 1];
	// 将第i个位置后的元素往前移
	for (int j = i;j < L.length; j++){
		L.data[j - 1] = L.data[j];
	}
	// 顺序表长度-1
	L.length--;
	return true;
}

总结

顺序表的查找

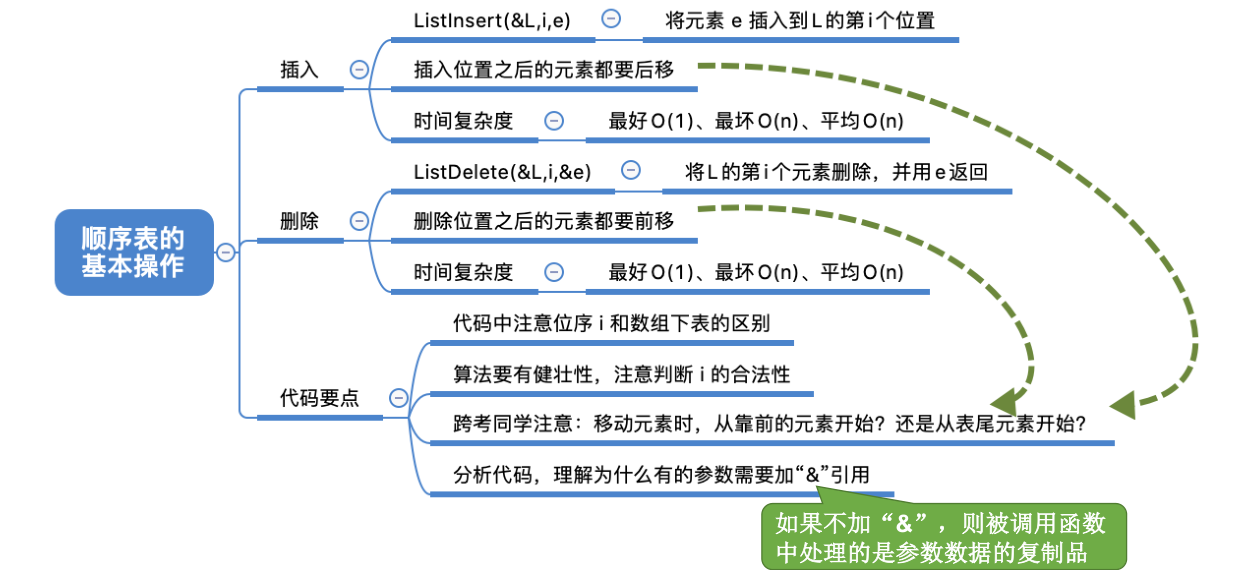
按位查找

• GetElem(L,i) ：按位查找操作。获取表 L 中第 i 个位置的元素的值。

// 和访问普通数组的方法一样
ElemType GetElem(SqList &L, int i){
	return L.data[i-1];
}

时间复杂度

由于顺序表的各个数据元素在内存中连续存放，因此可以根据起始地址和数据元素大小立即找到第 i 个元素 ——“随机存取” 特性

时间复杂度： $O(1)$

按值查找

• LocateElem(L,e) ：按值查找操作。在表 L 中查找具有给定关键字值的元素。

//在顺序表L中查找第一个元素值等于e的元素，并返回其位序
int LocateElem(SeqList &L,ElemType e){
    for(int i=0;i<L.length;i++){
    	if(L.data[i]==e){
            return i+1;  //数组下标为i的元素值等于e，返回其位序i+1
        }
    }
    return 0;  //退出循环，说明查找失败
}

时间复杂度

• 最好情况：目标元素在表头

  循环 1 次；最好时间复杂度 = O (1)

• 最坏情况：目标元素在表尾 循环 n 次；最坏时间复杂度 = O (n);

• 平均情况：假设目标元素出现在任何一个位置的概率相同，都是 $\frac{1}{n}$ 目标元素在第 1 位，循环 1 次；在第 2 位，循环 2 次；…… ；在第 n 位，循环 n 次 平均循环次数 $=1\cdot \frac{1}{\mathrm{n}}+2\cdot \frac{1}{\mathrm{n}}+3\cdot \frac{1}{\mathrm{n}}+\dots \dots +\mathrm{n}\cdot \frac{1}{\mathrm{n}}=\frac{n(n+1)}{2}\frac{1}{\mathrm{n}}=\frac{n+1}{2}\Rightarrow$ 平均时间复杂度 $ = O (n)$

总结

单链表

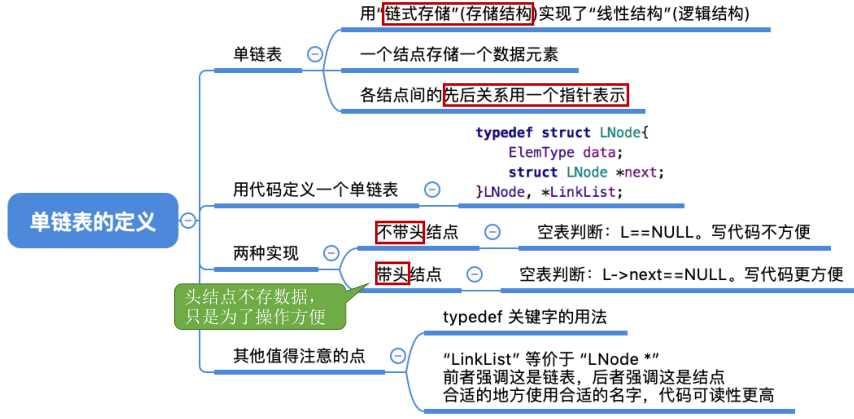
单链表的定义

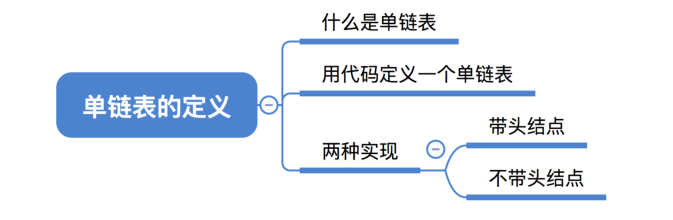
什么是单链表

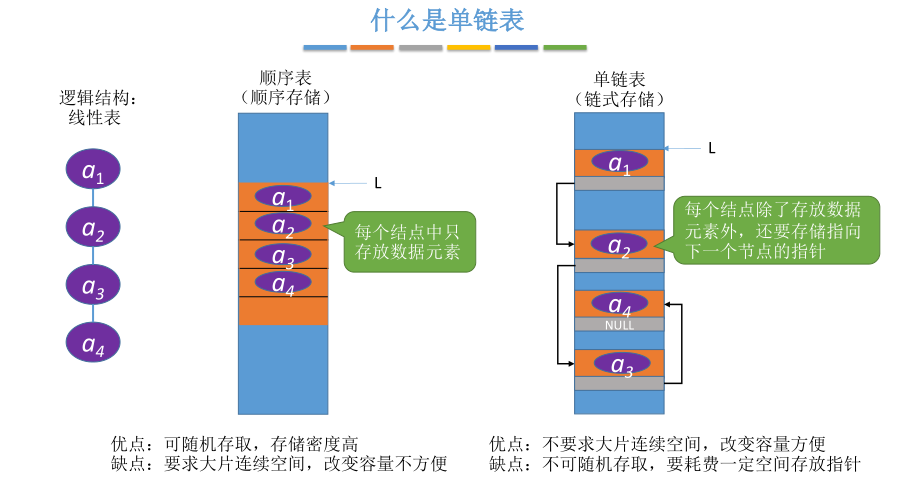
用代码定义一个单链表

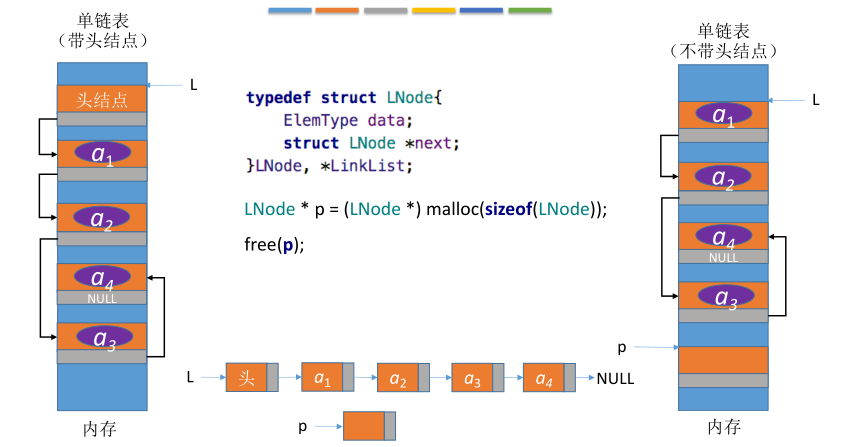
typedef struct LNode{ // 定义单链表结点类型
    ElemType data; // 每个节点存放一个元素
    struct LNode *next; // 指针指向下一个结点
}LNode, *LinkList;
//等价于上者，我们通常使用上者更为方便
struct LNode{ // 定义单链表结点类型
    ElemType data; // 每个节点存放一个元素
    struct LNode *next; // 指针指向下一个结点
}
typedef struct LNode LNode;
typedef struct LNode *LinkList;

要表示一个单链表时，只需声明一个头指针 L ，指向单链表的第一个结点

LNode * L; //声明一个指向单链表第一个结点的指针
LinkList L; //与上者相同，但可读写更强

* 那么何时用 LNode ，何时用 LinkList 表示呢？

typedef struct LNode{ // 定义单链表结点类型
    ElemType data; // 每个节点存放一个元素
    struct LNode *next; // 指针指向下一个结点
}LNode, *LinkList;

LNode * GetElem(LinkList L,int i){
    int j=1;
    LNode *p=L->next;
    if(i==0){
        return L;
    }
    if(i<1){
        return NULL;
    }
    while(p!=NULL& j<i){
        p=p->next;
        j++;
    }
    return p;
}

如上述代码中的 GetElem 函数，当强调这是一个单链表 —— 使用 LinkList，当强调这是一个结点 —— 使用 LNode *。

不带头结点的单链表

typedef struct LNode{ // 定义单链表结点类型
    ElemType data; // 每个节点存放一个元素
    struct LNode *next; // 指针指向下一个结点
}LNode, *LinkList;

//初始化一个空的单链表
bool InitList(LinkList &L){
    L = NULL; //设置为NULL防止脏数据
    return true;
}

// 判断单链表是否为空
bool Empty(LinkList L){
    return (L==NULL);
}

void test(){
    LinkList L; //声明一个指向单链表的指针，并没有初始化
    InitList(L); // 初始化
}

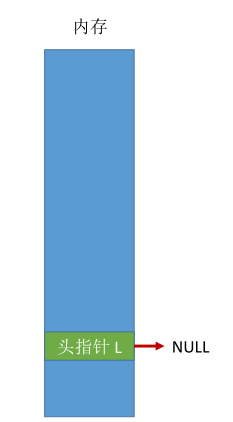
带头节点的单链表

typedef struct LNode{ // 定义单链表结点类型
    ElemType data; // 每个节点存放一个元素
    struct LNode *next; // 指针指向下一个结点
}LNode, *LinkList;

//初始化一个单链表（带头节点）
bool InitList(LinkList &L){
    L = (LNode *) malloc(sizeof(LNode)); // 分配一个头结点
    if(L==NULL){
        return false;
    }
    L->next = NULL; //头结点之后暂时还没有节点
    return true;
}

// 判断单链表是否为空（带头节点）
bool Empty(LinkList L){
    if(L->next ==NULL){
        return true;
    } else {
        return false;
    }
}

void test(){
    LinkList L; //声明一个指向单链表的指针
    InitList(L); //初始化
}

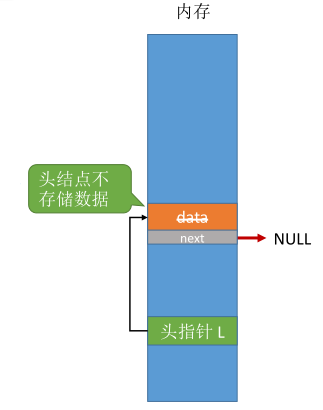
不带头结点 V.S. 带头结点

不带头结点，写代码更麻烦对第一个数据结点和后续数据结点的处理需要用不同的代码逻辑对空表和非空表的处理需要用不同的代码逻辑。一般我们使用带头结点的链表。

总结

单链表的插入和删除

按位序插入

带头结点

• ListInsert(&L,i,e) ：插入操作。在表 L 中的第 i 个位置上插入指定元素 e。

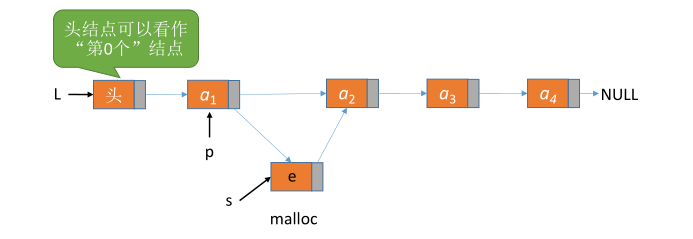
// 在第 i 个位置插入元素e（带头节点） 
bool ListInsert(LinkList &L, int i, ElemType e) {
	if (i < 1) {
		return false;
	}
	LNode *p; // 指针p指向当前扫描的结点 
	int j = 0; // 当前p指向的是第几个结点 
	p = L; // L指向头节点，头节点是第0个结点（不存数据） 
	while (p != NULL && j < i - 1) { // 循环找到第i-1个结点
		p = p->next;
		j++;
	}
	if (p == NULL) { // i值不合法 
		return false;
	}
	LNode *s = (LNode *)malloc(sizeof(LNode));
	s->data = e;
	s->next = p->next; 
	p->next = s; // 将结点s连到p之后 
	return true;
}

不带头结点

• ListInsert(&L,i,e) ：插入操作。在表 L 中的第 i 个位置上插入指定元素 e。

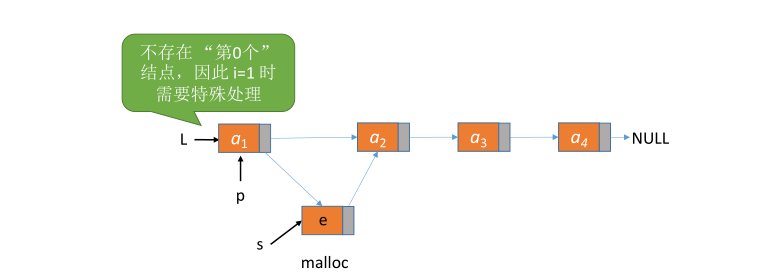
// 在第 i 个位置插入元素e（不带头节点）
bool ListInsert(LinkList &L, int i, ElemType e) {
	if (i < 1) {
		return false;
	}
	if (i == 1) {
		LNode *s = (LNode *)malloc(sizeof(LNode));
		s->data = e;
		s->next = L;
		L = s; //头指针指向新节点
		return true;
	}
	LNode *p; // 指针p指向当前扫描的结点
	int j = 1; // 当前p指向的是第几个结点
	p = L; // p指向第一个结点（注意：不是头结点）
	while (p != NULL && j < i - 1) {
		p = p->next;
		j++;
	}
	if (p == NULL) { // i值不合法
		return false;
	}
	LNode *s = (LNode *)malloc(sizeof(LNode));
	s->data = e;
	s->next = p->next;
	p->next = s; // 将结点s连到p之后
	return true;
}

指定节点后插

// 后插操作：在p结点之后插入元素e
bool InsertNextNode(LNode *p, ElemType e) {
	if (p == NULL) {
		return false;
	}
	LNode *s = (LNode *)malloc(sizeof(LNode));
	if (s == NULL) { // 内存分配失败，如内存不足等
		return false;
	}
	s->data = e; // 用结点s保存数据元素e
	s->next = p->next;
	p->next = s; // 将结点s连到p之后
	return true;
}

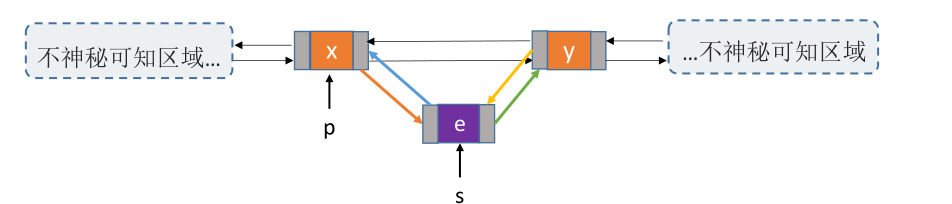
指定节点前插

一种是在方法参数中传入头指针，寻找指定节点的前驱，再进行插入。

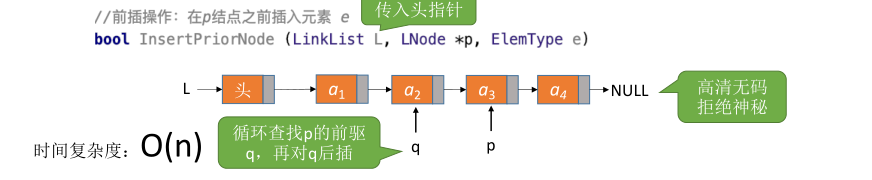
一种是插入节点先后插到指定节点后面，然后再与指定节点的值进行替换。

// 前插操作：在p结点之前插入元素e
bool InsertPriorNode(LNode *p, ElemType e) {
	if (p == NULL) {
		return false;
	}
	LNode *s = (LNode *)malloc(sizeof(LNode));
	if (s == NULL) { // 内存分配失败，如内存不足等
		return false;
	}
	s->next = p->next;
	p->next = s; // 新结点s连到p之后
	s->data = p->data; // 将p中元素复制到s中
	p->data = e; // p中元素覆盖为e
	return true;
}

按位序删除

按位序删除（带头结点）

• ListDelete(&L,i,&e) ：删除操作。删除表 L 中第 i 个位置的元素，并用 e 返回删除元素的值。

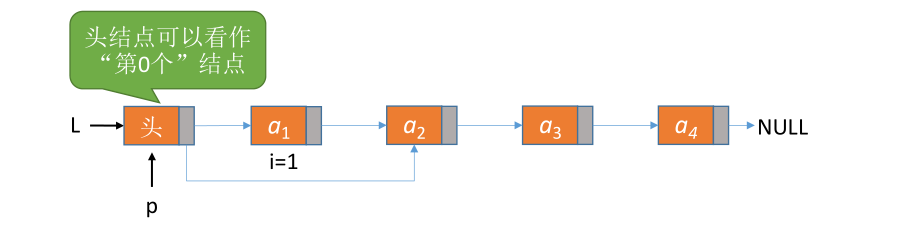
// 按位序删除（带头结点）
bool ListDelete(LinkList &L, int i, ElemType &e) {
	if (i < 1) {
		return false;
	}
	LNode *p; // 指针p指向当前扫描到的结点
	int j = 0; // 当前p指向是第几个结点
	p = L; // L指向头结点，头结点是第0个结果（不存储数据）
	while (p != NULL && j < i-1) { // 循环找到第 i-1 个结点
		p = p->next;
		j++;
	}
	if (p == NULL) { // i值不合法
		return false;
	}
	if (p->next == NULL) { // 第i-1个结点之后没有其他结点
		return false;
	}
	LNode *q = p->next; //令q指向被删除的结点
	e = q->data; //用e返回被删除结点元素的值
	p->next = q->next; //将q结点从链表中断开 即p的next指向q的next
	free(q); //释放q结点
	return true;
}

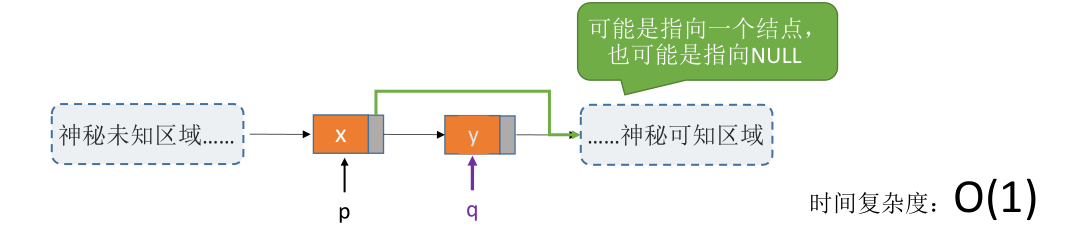
指定结点删除

// 指定结点删除
bool DeleteNode(LNode *p) {
	if (p == NULL) {
		return false;
	}
	// 要注意这种方法只保证要删除的结点后有后继结点，如果没有后继，需要传递头结点进行遍历链表删除
	LNode *q = p->next; // 令q指向p结点的后继结点
	p->data = p->next->data; // p结点与后继结点交换数据源 p结点成了它的后继结点（偷天换日
	// 接下来我们只需要删除原来的q结点即可
	p->next = q->next; // q结点从链表中 断开
	free(q);
	return true;
}

总结

单链表查找

按位查找

• GetElem(L,i) ：按位查找操作。获取表 L 中第 i 个位置的元素的值。

// 按位查找，返回第 i 个元素（带头结点）
LNode * GetElem(LinkList L, int i) {
	if (i < 0) {
		return NULL;
	}
	LNode *p; // 指针p指向当前扫描的结点
	int j = 0; // 当前p指向是第几个结点
	p = L; // L指向头结点 头结点是第0个结点（不存储数据）
	while (p != NULL && j < i) { // 循环找到第 i 个结点
		p = p->next;
		j++;
	}
	return p;
}

按值查找

• LocateElem(L,e) ：按值查找操作。在表 L 中查找具有给定关键字值的元素。

// 按值查找，返回指定值的元素
LNode * LocateElem(LinkList L, ElemType e) {
	LNode *p = L->next;
	while (p != NULL && p->data != e) {
		p = p->next;
	}
	return p;
}

求表长度

// 求表的长度
int Length(LinkList L){
	int len =0;
	LNode *p=L;
	while(p->next !=NULL){
		p=p->next;
		len++;
	}
	return len;
}

总结

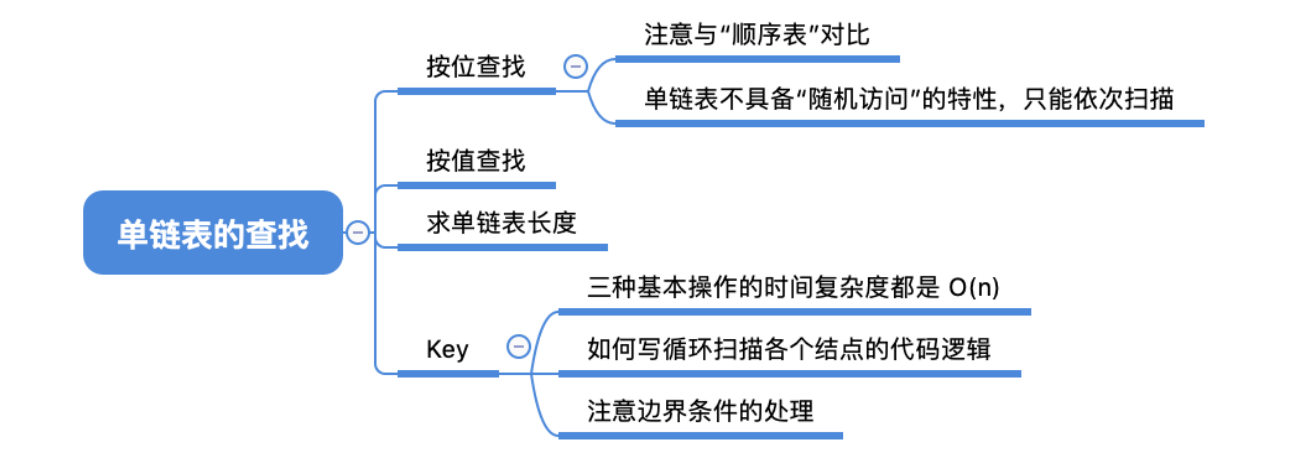
单链表建立

尾插法

// 后插法：在p结点之后插入元素e
LinkList List_TailInsert(LinkList &L) {
	int x;
	L = (LinkList)malloc(sizeof(LNode)); //建立头结点
	LNode *s, *r = L; //r为表尾指针
	scanf("%d", &x);
	while (x != 9999) {
		s = (LNode *)malloc(sizeof(LNode)); // 创建新的结点
		s->data = x;
		r->next = s; //尾结点的后继指向插入的结点
		r = s; //r重新指向新的尾结点
		scanf("%d", &x);
	}
	r->next = NULL;
	return L;
}

头插法

// 头插法
LinkList List_HeadInsert(LinkList &L) {
	LNode *s;
	int x;
	L = (LinkList)malloc(sizeof(LNode)); //建立头结点
	L->next = NULL;
	scanf("%d", &x);
	while (x != 9999) {
		s = (LNode *)malloc(sizeof(LNode)); // 创建新的结点
		s->data = x;
		s->next = L->next;
		L->next = s; // 将新结点插入表中，L为头指针
		scanf("%d", &x);
	}
	return L;
}

双链表

双链表：可进可退，存储密度更低一丢丢

typedef struct DNode
{
	ElemType data;
	struct DNode *prior, *next; //包含前驱和后继指针
} DNode, *DLinklist;

双链表的初始化（带头结点）

// 初始化双链表
bool InitDlinkList(DLinklist &L) {
	L = (DNode *)malloc(sizeof(DNode));
	if (L == NULL) {
		return false;
	}
	L->prior = NULL;
	L->next = NULL;
	return true;
}

// 判断双链表是否为空（带头结点）
bool Empty(DLinklist L) {
	if (L->next == NULL) {
		return true;
	} else {
		return false;
	}
}

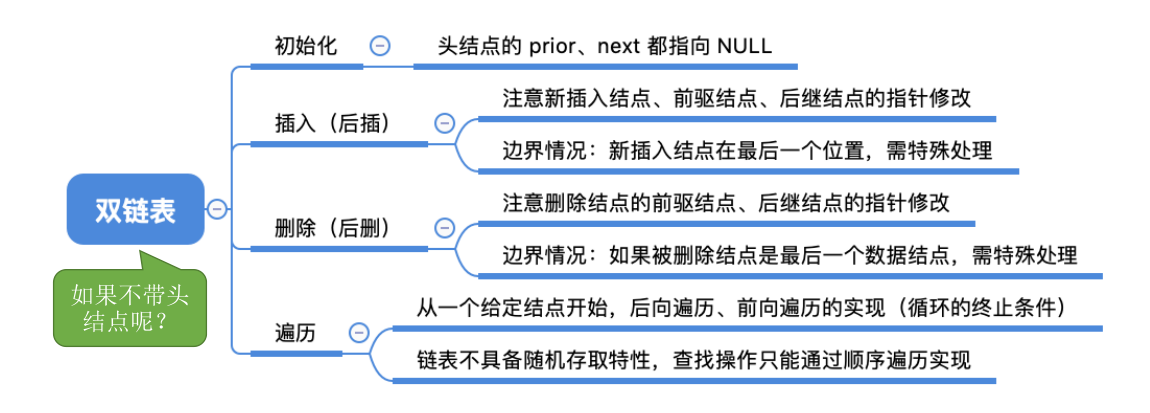
双链表的插入

// 在p结点之后插入s结点
bool InsertNextDNode(DNode *p, DNode *s) {
	if (p == NULL || s == NULL) {
		return false;
	}
	s->next = p->next; //将结点s插入到结点p之后
	if (p->next != NULL) { // 如果p结点有后继结点
		p->next->prior = s;
	}
	s->prior = p;
	p->next = s;
	return true;
}

双链表的删除

// 删除p结点的后继结点
bool DeleteNextDNode(DNode *p) {
	if (p == NULL) {
		return false;
	}
	DNode *q = p->next; //找p的后继结点
	if (q == NULL) { //p没有后继
		return false;
	}
	p->next = q->next; //p的后继指向 p的后继的后继
	if (q->next != NULL) { // 如果q的后继确实存在 则需要把q的后继的前驱改为p
		q->next->prior = p;
	}
	free(q);
	return true;
}

总结

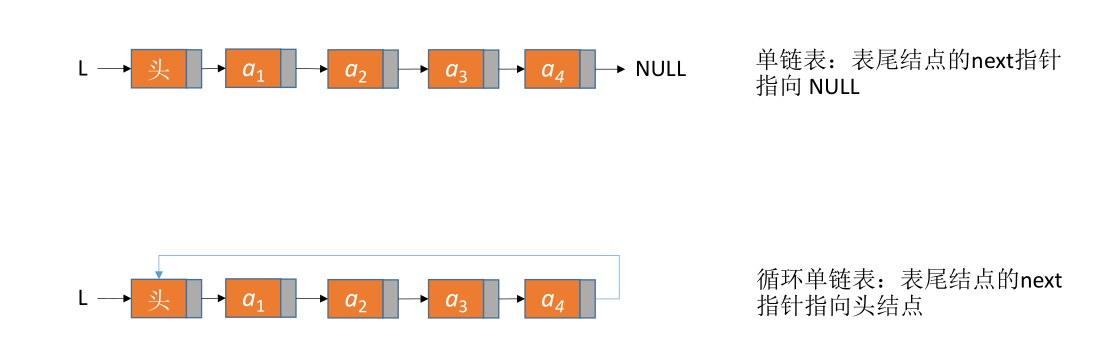
循环链表

循环单链表

typedef struct LNode
{
	ElemType data;
	struct LNode *next;
} LNode, *LinkList;

// 初始化一个循环单链表
bool InitList(LinkList &L) {
	L = (LNode *)malloc(sizeof(LNode));
	if (L == NULL) {
		return false;
	}
	L->next = L; // 头结点next指向头结点
	return true;
}

// 判断结点p是否为循环链表的表尾结点
bool isTail(LinkList L, LNode *p) {
	if (p->next == L) {
		return true;
	} else {
		return false;
	}
}

• 单链表：从一个结点出发只能找到后续的各个结点
• 循环单链表：从一个结点出发可以找到其他任何一个结点

循环双链表

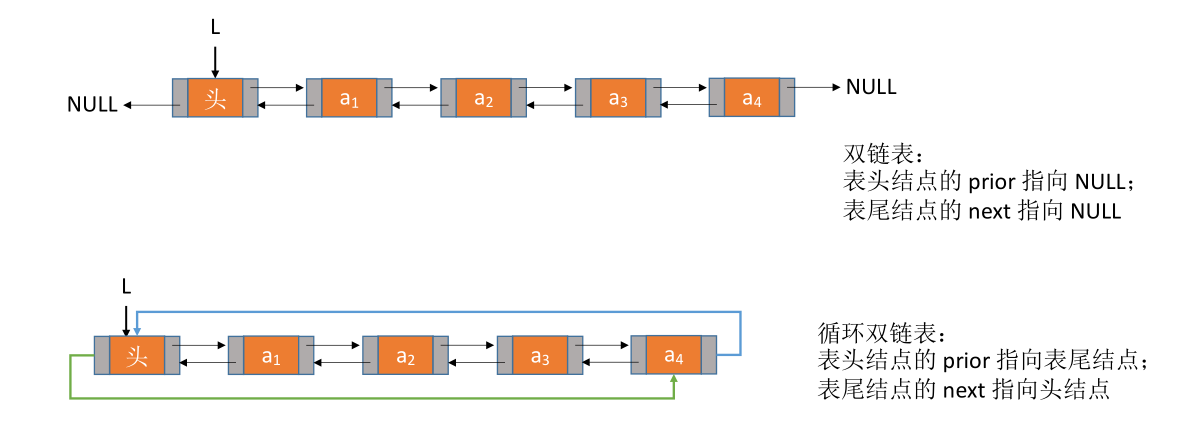
typedef struct DNode
{
	ElemType data;
	struct DNode *prior, *next; //包含前驱和后继指针
} DNode, *DLinklist;

// 初始化双链表
bool InitDlinkList(DLinklist &L) {
	L = (DNode *)malloc(sizeof(DNode));
	if (L == NULL) {
		return false;
	}
	L->prior = L; //头结点的prior指向头结点
	L->next = L; //头结点的next指向头结点
	return true;
}

// 判断双链表是否为空
bool Empty(DLinklist L) {
	if (L->next == NULL) {
		return true;
	} else {
		return false;
	}
}

// 判断结点p是否为循双环链表的表尾结点
bool isTail(LinkList L, LNode *p) {
	if (p->next == L) {
		return true;
	} else {
		return false;
	}
}

总结

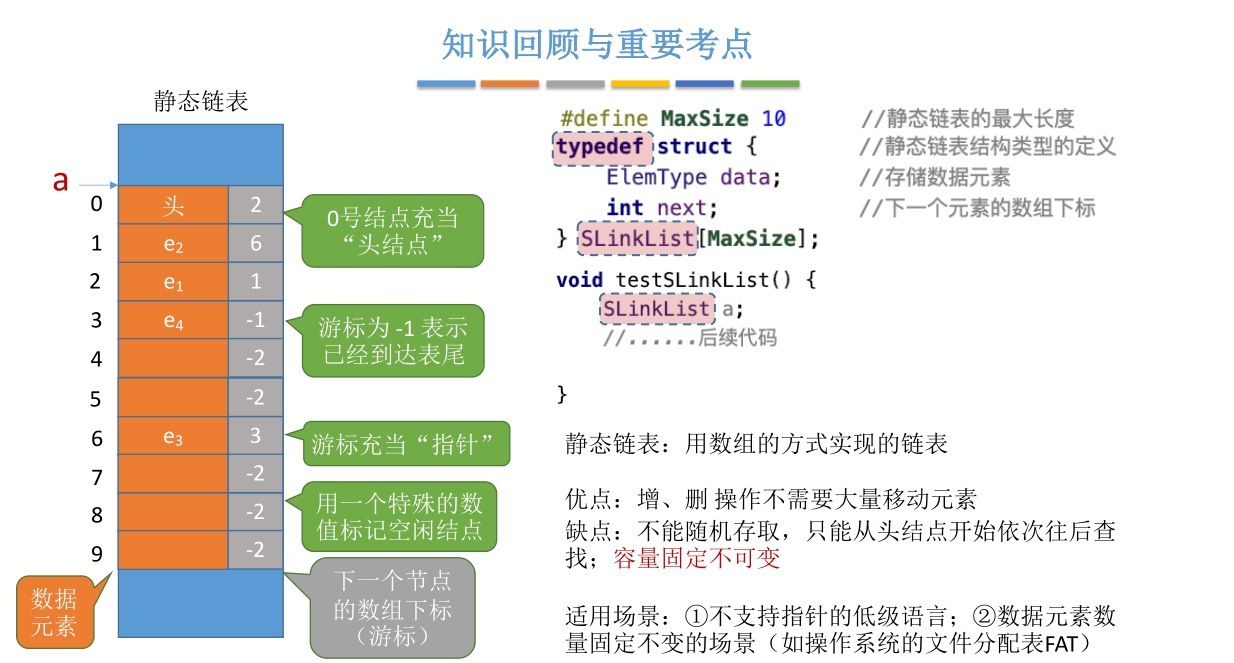
静态链表

什么是静态链表

• 单链表：各个结点在内存中星罗棋布、散落天涯。
• 静态链表：分配一整片连续的内存空间，各个结点集中安置。

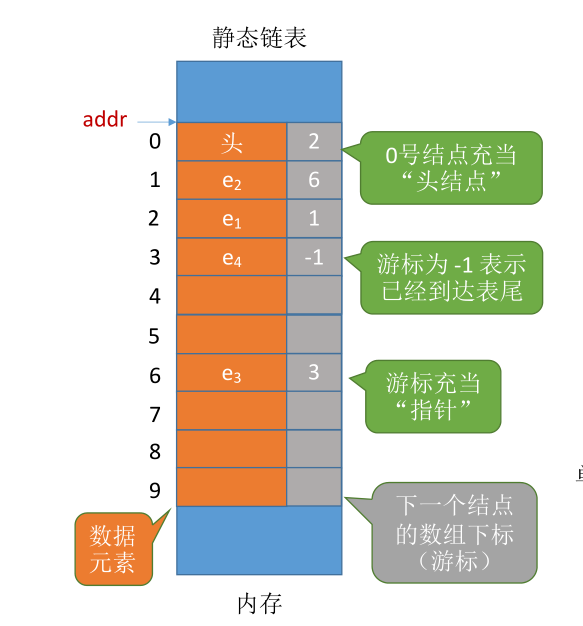
每个数据元素 4B，每个游标 4B（每个结点共 8B）。设起始地址为 addr，$e_1$ 的存放地址为 $addr+8\ast 2$

定义一个静态链表

#define MaxSize 10 //静态链表最大长度
struct Node
{
	ElemType data; //存储数据元素
	int next; //下一个元素的数组下标
};
typedef struct Node SLinkList[MaxSize];

void testLinkList(){
	struct Node a[MaxSize];
}

// Node和Node2两者等价

struct Node2
{
	ElemType data; //存储数据元素
	int next; //下一个元素的数组下标
} SLinkList[MaxSize];

void testLinkList2(){
	SLinkList a;
}

基本操作

初始化

初始化静态链表：把 a [0] 的 next 设为 -1，把其他结点的 next 设为一个特殊值用来表示结点空闲，如 -2

查找

从头结点出发挨个往后遍历结点

插入

插入位序为 i 的结点：

1. 找到一个空的结点，存入数据元素
2. 从头结点出发找到位序为 i-1 的结点
3. 修改新结点的 next
4. 修改 i-1 号结点的 next

删除

删除某个结点：

1. 从头结点出发找到前驱结点
2. 修改前驱结点的游标
3. 被删除结点 next 设为 -2

总结

顺序表和链表比较

逻辑结构

都属于线性表，都是线性结构

• 顺序表（顺序存储）

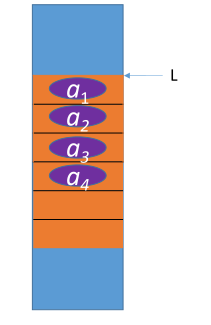
  • 优点：支持随机存取、存储密度高
  • 缺点：大片连续空间分配不方便，改变容量不方便

• 链表（链式存储）

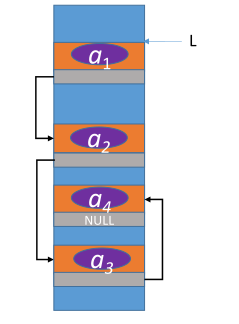
  • 优点：离散的小空间分配方便，改变容量方便

  • 缺点：不可随机存取，存储密度低 $\text{存储密度}=\frac{\text{结点数据本身所占的存储量}}{\text{结点结构所占的存储总量}}$

    typedef struct node{
        char data[16];
        struct node *next;
    } LinkStrNode
    

    以上定义了一个数据结点，这个结点包括两个部分，数据部分：data [16], 这是一个字符数组，占 16 个字节，非数据部分：*next , 是一个结点指针，设占 4 个字节，

    则以上的存储密度为$\frac{16}{16+4}=80\mathrm{\%}$

基本操作

创建

• 顺序表：需要预分配大片连续空间。若分配空间过小，则之后不方便拓展容量；若分配空间过大，则浪费内存资源
  • 静态分配：静态数组；容量不可改变
  • 动态分配：动态数组（malloc、free）；容量可改变，但需要移动大量元素，时间代价高
• 链表：只需分配一个头结点（也可以不要头结点，只声明一个头指针），之后方便拓展

销毁

• 顺序表：修改 Length = 0
  • 静态分配：静态数组；系统自动回收空间
  • 动态分配：动态数组（malloc、free）；需要手动 free，需要注意是 malloc 和 free 需要成对出现。
• 链表：依次删除各个结点（free）

插入和删除

• 顺序表：插入 / 删除元素要将后续元素都后移 / 前移，时间复杂度 O (n)，时间开销主要来自移动元素，若数据元素很大，则移动的时间代价很高。
• 链表：插入 / 删除元素只需修改指针即可，时间复杂度 O (n)，时间开销主要来自查找目标元素，查找元素的时间代价更低。

查询

• 顺序表：
  • 按位查找：O (1)
  • 按值查找：O (n) 若表内元素有序，可在 O (log 2 n) 时间内找到（二分查找）
• 链表：
  • 按位查找：O (n)
  • 按值查找：O (n)

总结

• 顺序表：表长可预估、查询（搜索）操作较多
• 链表：表长难以预估、经常要增加 / 删除元素

操作	顺序表	链表
弹性（可扩容）	不支持	支持
增、删	慢	快
查	快	慢