Chiriri's blog
Iekr
2023-11-11
目录

算法

# 算法

# 链表

# 146. LRU 缓存 (opens new window)

tag： 字节 、 核桃编程

count：18

as：LRU 算法，什么原理，怎么实现

lru 设计、保证线程安全

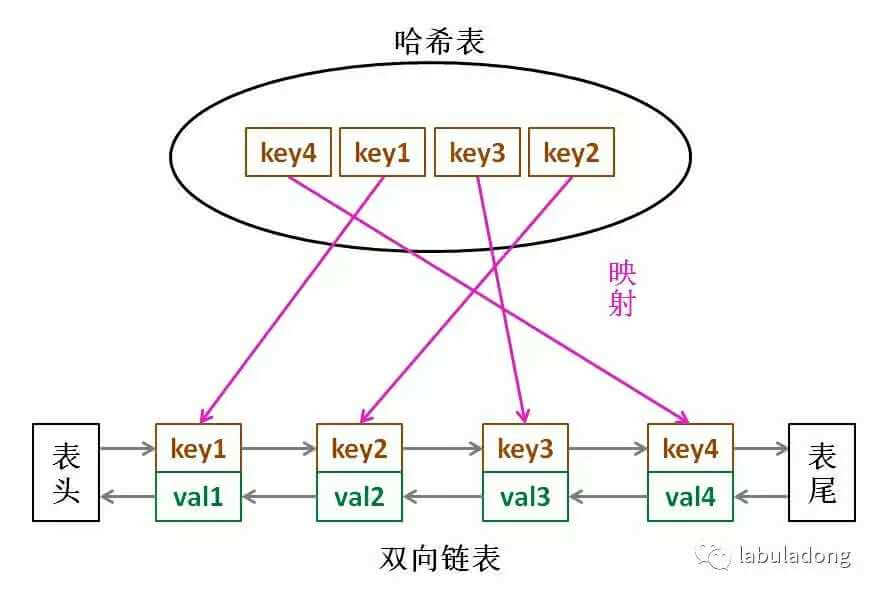
LRU 缓存算法的核心数据结构就是哈希链表，双向链表和哈希表的结合体。这个数据结构长这样：

img

put 方法

img

import java.util.HashMap;

//leetcode submit region begin(Prohibit modification and deletion)
class LRUCache {
    HashMap<Integer,Node> map = new HashMap<>();
    DoubleList cache = new DoubleList();
    int capacity;
    public LRUCache(int capacity) {
        this.capacity=capacity;
    }

    public int get(int key) {
        // 查看map缓存是否有此key
        if(!map.containsKey(key)){
            // 没有此key
            return -1;
        }
        // key存在，则将该节点提升到最近使用过的节点 即将该节点移到链尾
        makeRecently(key);
        // 返回该节点的值
        return map.get(key).val;

    }

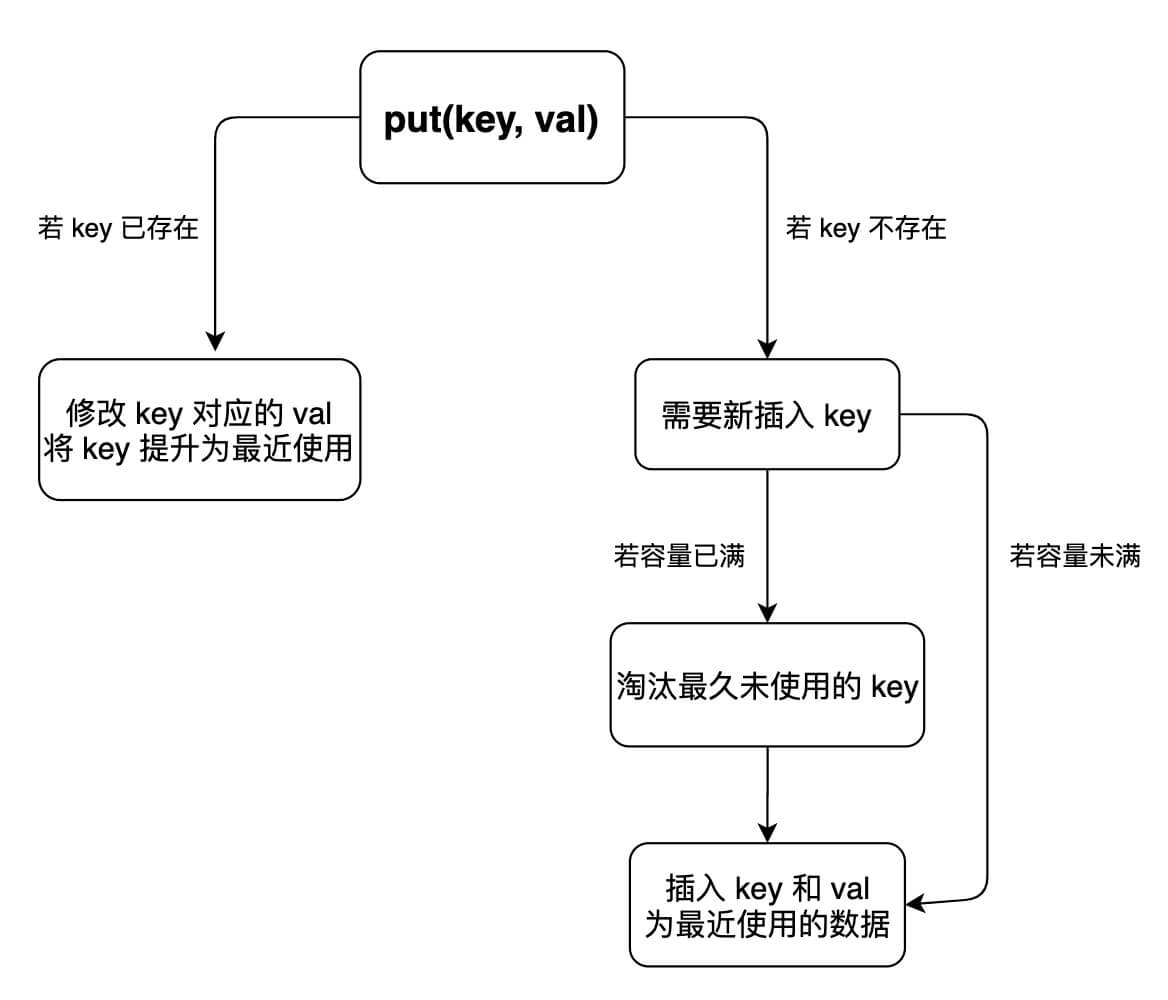
    public void put(int key, int value) {
        // 缓存中存在此key 进行更新操作
        if(map.containsKey(key)){
            // 从链表中删除该节点
            deleteKey(key);
            // 重新加入到链尾中 即可变为最近使用的节点
            addRecently(key,value);
            return;
        }

        // 如果插入操作导致关键字数量超过 capacity ，则应该 逐出 最久未使用的关键字。
        // 先判断是否等于 capacity 再进行移除最久未使用的，再进行 put 操作
        if (capacity==cache.size){
            removeLeastRecently();
        }

        // put添加到链尾
        addRecently(key,value);
    }

    // 提升该节点为最近的使用的节点
    public void makeRecently(int key){
        // 从map中获取该节点
        Node node = map.get(key);
        // 从链表中删除该节点
        cache.remove(node);
        // 再从链尾中添加 链尾为最近使用过的节点 而链头为最少使用的节点
        cache.addLast(node);
    }

    // 添加为最近使用的节点
    public void addRecently(int key,int val){
        Node node = new Node(key, val);
        // 添加到链尾
        cache.addLast(node);
        // 将节点缓存到map中
        map.put(key,node);
    }

    // 删除指定key
    public void deleteKey(int key){
        Node node = map.get(key);
        // 从链表中删除节点
        cache.remove(node);
        // 再从map中删除节点
        map.remove(key);
    }

    // 删除最少使用的节点
    public void removeLeastRecently(){
        // 头节点为最少使用的节点
        Node node = cache.removeFirst();
        // 获取头节点的key
        int key = node.key;
        // 从map中删除该节点的缓存
        map.remove(key);
    }
}

class Node {
    int key,val;
    Node next,prev;
    public Node(int k,int v){
        key=k;
        val=v;
    }
}

class DoubleList{
    private Node  head,tail;
    int size;

    public DoubleList(){
        head=new Node(0,0);
        tail=new Node(0,0);
        head.next=tail;
        tail.prev=head;
        size=0;
    }

    // 添加为头节点
    public void addLast(Node x){
        x.prev=tail.prev;
        x.next=tail;
        tail.prev.next=x;
        tail.prev=x;
        size++;
    }

    // 删除指定节点
    public void remove(Node x){
        x.prev.next=x.next;
        x.next.prev=x.prev;
        size--;
    }

    // 删除并返回头节点
    public Node removeFirst(){
        if(head.next==tail){
            return null;
        }
        Node fist = head.next;
        remove(fist);
        return fist;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130

当然我们可以使用 Java 的内置类型 LinkedHashMap 来实现 LRU 算法，逻辑和之前完全一致

import java.util.LinkedHashMap;

//leetcode submit region begin(Prohibit modification and deletion)
class LRUCache {

    int capacity;
    LinkedHashMap<Integer,Integer> cache = new LinkedHashMap<>();

    public LRUCache(int capacity) {
        this.capacity=capacity;
    }
    
    public int get(int key) {
        // 获取前先判断是否存在缓存中
        if(!cache.containsKey(key)){
            return -1;
        }
        // 存在则将该节点提升为最近使用的节点 即将该节点移到链尾
        makeRecently(key);
        // 返回节点的值
        return cache.get(key);
    }
    
    public void put(int key, int value) {
        // 该key已经存在缓存中
        if(cache.containsKey(key)){
            // 修改该节点的值
            cache.put(key,value);
            // 将该节点提升到最近使用的
            makeRecently(key);
            return;
        }
        // 如果插入操作导致关键字数量超过 capacity ，则应该 逐出 最久未使用的关键字。
        if (cache.size()>=capacity){
            // 获取链头，链头为最久未使用的节点
            int oldesKey = cache.keySet().iterator().next();
            // 从缓存冲移除最久未使用的节点
            cache.remove(oldesKey);
        }
        // 再进行 put 操作
        cache.put(key,value);
    }

    public void makeRecently(int key){
        // 从缓存中获取节点
        int val = cache.get(key);
        // 从链表中移除该节点
        cache.remove(key);
        // 再重新进入到链尾中提升为最近使用的节点
        cache.put(key,val);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

# 206. 反转链表 (opens new window)

tag：

count：8

as：

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode reverseList(ListNode head) {
        ListNode next = null;
        ListNode pre = null;
        while(head != null){
            next = head.next;
            head.next = pre;
            pre = head;
            head = next;
        }
        return pre;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

# 92. 反转链表 II (opens new window)

tag：

count：1

as：

# 25. K 个一组翻转链表 (opens new window)

class Solution {
		public ListNode reverseKGroup(ListNode head, int k) {
			ListNode start = head; // 缓存当前链表头
			ListNode end = getKEnd(start, k); // 获取第一组链表尾
			if (end == null) { // 如果k个元素内没有链尾 说明第一组链表＜=k个元素 无法进行反转 直接返回当前链表即可
				return head;
			}
			// 第一组满足k个元素进行反转
			head = end; // 将当前链表头指向链表尾的元素
			reverse(start, end); // 进行反转
			ListNode lastEnd = start; // 上一组节点尾
			while (lastEnd.next != null) {
				start = lastEnd.next; // 缓存当前组的链表头
				end = getKEnd(start, k); // 获得当前组的链表尾
				if (end == null) {
					return head;
				}
				reverse(start, end); // 满足k个 反转当前组
				lastEnd.next = end; // 将上组的链尾 指向 当前组反转后的链表
				lastEnd = start; // 更新lastEnd为当前组的链尾
			}
			return head;

		}

		public ListNode getKEnd(ListNode pre, int k) {
			while (--k != 0 && pre != null) { // 返回当前组的最后一个元素(即新的链头)
				pre = pre.next;
			}
			return pre;
		}

		public void reverse(ListNode start, ListNode end) {
			end = end.next; // 将当前end向后移一位(即下一组的链头,下一组未反转)
			ListNode cur = start; // 当前元素
			ListNode pre = null; // 缓存上次的修改过元素
			ListNode next = null; // 下一跳元素
			while (cur != end) {
				next = cur.next; // 缓存下一跳
				cur.next = pre; // 指向上次修改后的元素
				pre = cur; // 更新修改后的元素
				cur = next; // 更新当前元素
			}
			start.next = end; // 将当前组链尾 指向下一组的链头
		}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

# 手写反转链表、返回链表倒数第 n 个数

tag： 携程

count：1

# 21. 合并两个有序链表 (opens new window)

tag： 知乎

count：1

# 82. 删除排序链表中的重复元素 II (opens new window)

tag： 途虎养车

count：1

# 滑动窗口

# 3. 无重复字符的最长子串 (opens new window)

class Solution {
    public int lengthOfLongestSubstring(String s) {
        if(s.length()==0){
            return 0;
        }
        HashMap<Character,Integer> map = new HashMap<>();
        int max=0,left=0;
        for(int i=0;i<s.length();i++){
            // 查看当前字符是否在map中
            if(map.containsKey(s.charAt(i))){
                // 存在则获取并更新为最大下标值  此下标+1为最长子串的开始 因为它之前的子串存在于map中
                left=Math.max(left,map.get(s.charAt(i))+1);
            }
            // 将当前字符和下标添加到map中
            map.put(s.charAt(i),i);
            // i为右指针，右指针减去left最长子串的开始下标+1 则为最长子串的长度
            max = Math.max(max,i-left+1);
        }
        return max;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

# 排序

# 215. 数组中的第 K 个最大元素 (opens new window)

# 分桶

class Solution {
    public int findKthLargest(int[] nums, int k) {
        int[] bucket = new int[20005];

        for(int n : nums) {
            bucket[n+10000]++;
        }

        for (int i=20004, sum = 0; i>=0; i--) {
            if ((sum += bucket[i]) >= k) {
                return i-10000;
            }
        }
        return 0;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

# 快排

根据快排改造的搜索，从子数组 a[l⋯r] 中选择任意一个元素 x 作为主元，调整子数组的元素使得左边的元素都小于等于它，右边的元素都大于等于它， x 的最终位置就是 q。 由此可以发现每次经过「划分」操作后，我们一定可以确定一个元素的最终位置，即 x 的最终位置为 q，并且保证 a[l⋯q−1] 中的每个元素小于等于 a[q]，且 $ a [q] $ 小于等于 a[q+1⋯r] 中的每个元素。所以只要某次划分的 q 为倒数第 k 个下标的时候，我们就已经找到了答案。 我们只关心这一点，至于 a[l⋯q−1] 和 $ a [q+1⋯r]$ 是否是有序的，我们不关心。

因此我们可以改进快速排序算法来解决这个问题：在分解的过程当中，我们会对子数组进行划分，如果划分得到的 q 正好就是我们需要的下标，就直接返回 $ a [q]$；否则，如果 q 比目标下标小，就递归右子区间，否则递归左子区间。这样就可以把原来递归两个区间变成只递归一个区间，提高了时间效率。这就是「快速选择」算法。

class Solution {
    int quickselect(int[] nums, int l, int r, int k) {
        if (l == r) return nums[k];
        int x = nums[l], i = l - 1, j = r + 1;
        while (i < j) {
            do i++; while (nums[i] < x);
            do j--; while (nums[j] > x);
            if (i < j){
                int tmp = nums[i];
                nums[i] = nums[j];
                nums[j] = tmp;
            }
        }
        if (k <= j) return quickselect(nums, l, j, k);
        else return quickselect(nums, j + 1, r, k);
    }
    public int findKthLargest(int[] _nums, int k) {
        int n = _nums.length;
        return quickselect(_nums, 0, n - 1, n - k);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

方式二：

「三路划分」，即每轮将数组划分为三个部分：小于、等于和大于基准数的所有元素。这样当发现第 k 大数字处在 “等于基准数” 的子数组中时，便可以直接返回该元素。

public class Solution {
    private int quickSelect(List<Integer> nums, int k) {
        // 随机选择基准数
        Random rand = new Random();
        int pivot = nums.get(rand.nextInt(nums.size()));
        // 将大于、小于、等于 pivot 的元素划分至 big, small, equal 中
        List<Integer> big = new ArrayList<>();
        List<Integer> equal = new ArrayList<>();
        List<Integer> small = new ArrayList<>();
        for (int num : nums) {
            if (num > pivot)
                big.add(num);
            else if (num < pivot)
                small.add(num);
            else
                equal.add(num);
        }
        // 第 k 大元素在 big 中，递归划分
        if (k <= big.size())
            return quickSelect(big, k);
        // 第 k 大元素在 small 中，递归划分
        if (nums.size() - small.size() < k)
            return quickSelect(small, k - nums.size() + small.size());
        // 第 k 大元素在 equal 中，直接返回 pivot
        return pivot;
    }
    
    public int findKthLargest(int[] nums, int k) {
        List<Integer> numList = new ArrayList<>();
        for (int num : nums) {
            numList.add(num);
        }
        return quickSelect(numList, k);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

# 堆

建立一个小根堆，根据当前队列元素个数或当前元素与栈顶元素的大小关系进行分情况讨论：

  • 当优先队列元素不足 k 个，可将当前元素直接放入队列中；
  • 当优先队列元素达到 k 个，并且当前元素大于栈顶元素（栈顶元素必然不是答案），可将当前元素放入队列中。
class Solution {
    public int findKthLargest(int[] nums, int k) {
        // 默认为小根堆
        PriorityQueue<Integer> q = new PriorityQueue<>((a,b)->a-b);
        for (int x : nums) {
            if (q.size() < k || q.peek() < x) q.add(x);
            // 维护一个 k 个大小的小根堆
            if (q.size() > k) q.poll();
        }
        // k个大小的小根堆 当前堆顶为第k个最大的数
        return q.peek();
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13

# 归并排序

tag：

count：1

as：给 10000 条数据，计算机一次只能处理 200 条，该如何排序

# 你了解那些排序算法，那些排序算法比较稳定

tag：

count：1

as：

# 快排

tag：

count：1

as：

# 56. 合并区间 (opens new window)

tag： 美团

count：1

as：

# 双指针

# 11. 盛最多水的容器 (opens new window)

class Solution {
    public int maxArea(int[] height) {
            int l = 0;
            int r  = height.length-1;
            int max=0;
            while(l<r){
                max = Math.max(max,(r-l)*Math.min(height[r],height[l]));
                if(height[l] < height[r]) l++;
                else r--;
                
            }
            return max;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

# 42. 接雨水 (opens new window)

class Solution {
    public int trap(int[] height) {
        if (height.length <= 2) return 0;
        int n = height.length;
        int[] maxLeft = new int[n];
        int[] maxRight = new int[n];
        
        // 记录每个柱子左边柱子最大高度
        maxLeft[0] = height[0];
        for (int i = 1; i < n; i++) {
            maxLeft[i] = Math.max(height[i], maxLeft[i - 1]);
        }
        // 记录每个柱子右边柱子最大高度
        maxRight[n - 1] = height[n - 1];
        for (int i = n - 2; i >= 0; i--) {
            maxRight[i] = Math.max(height[i], maxRight[i + 1]);
        }
        // 求和
        int sum = 0;
        for (int i = 0; i < n; i++) {
            int count = Math.min(maxLeft[i], maxRight[i]) - height[i];
            if (count > 0) sum += count;
        }
        return sum;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

# 二叉树

# 二叉树深度优先和广度优先

tag： 携程

count：2

# 109. 有序链表转换二叉搜索树 (opens new window)

tag： 字节

count：1

as：

# 打印二叉树从根节点到指定节点的路径

tag： Meta App

count：1

as：

# 图

# 动态规划

# 斐波那契

tag： 腾讯 、 小米 、 携程

count：3

as：

# 递归版本

# 动态规划

# 分析递归时间复杂度，空间复杂度

# 两个版本优缺点

# 栈

# 20. 有效的括号 (opens new window)

编辑 (opens new window)
上次更新: 2025/01/01, 10:09:39
操作系统
Hadoop

← Hadoop→

最近更新
01
k8s
06-06
02
进程与线程
03-04
03
计算机操作系统概述
02-26
更多文章>
Theme by Vdoing | Copyright © 2022-2025 Iekr | Blog