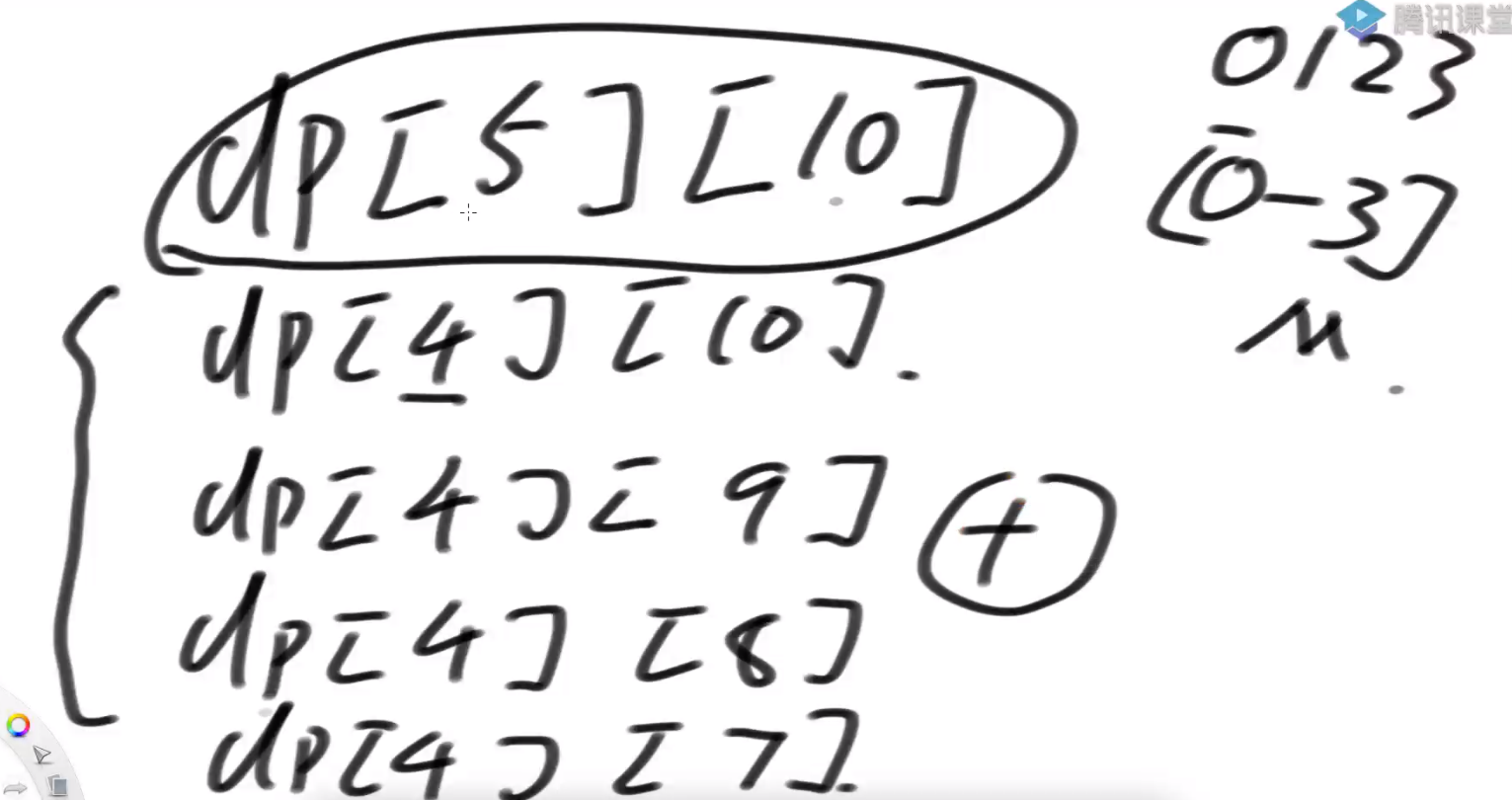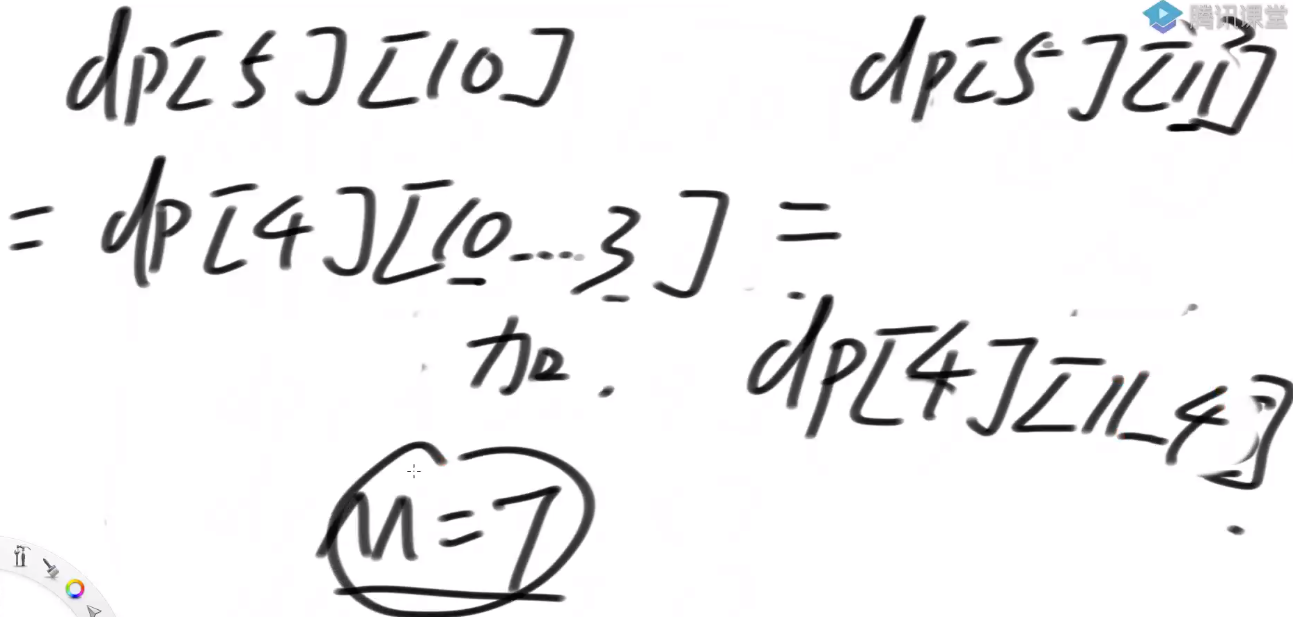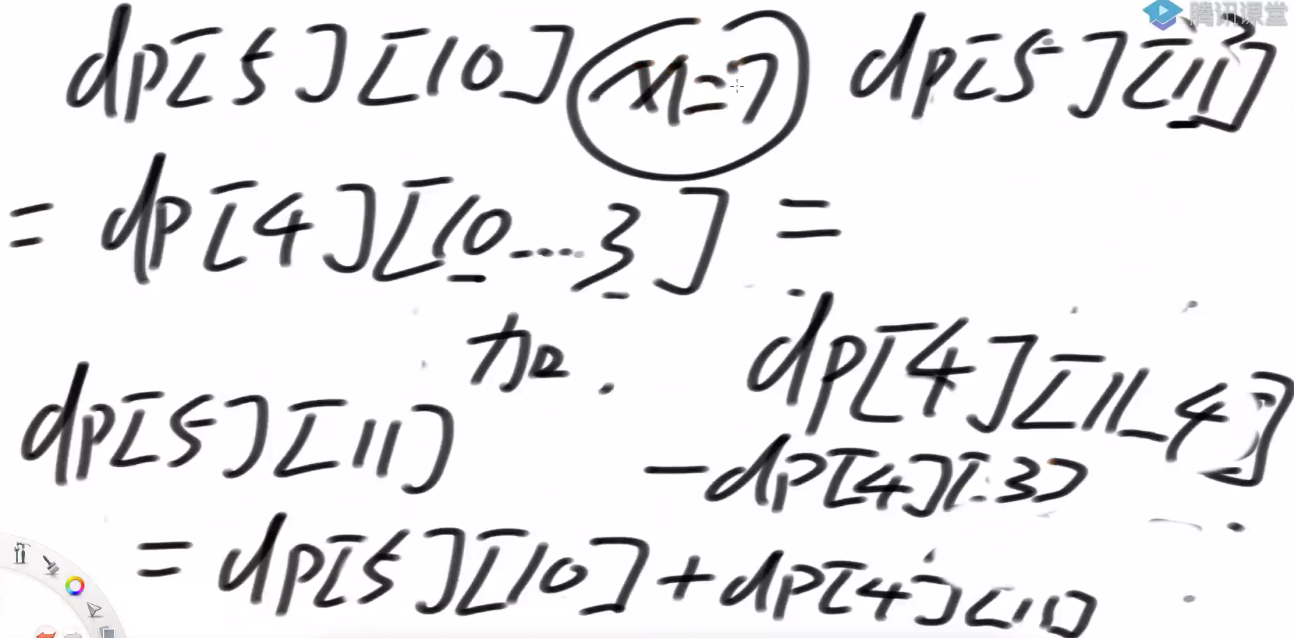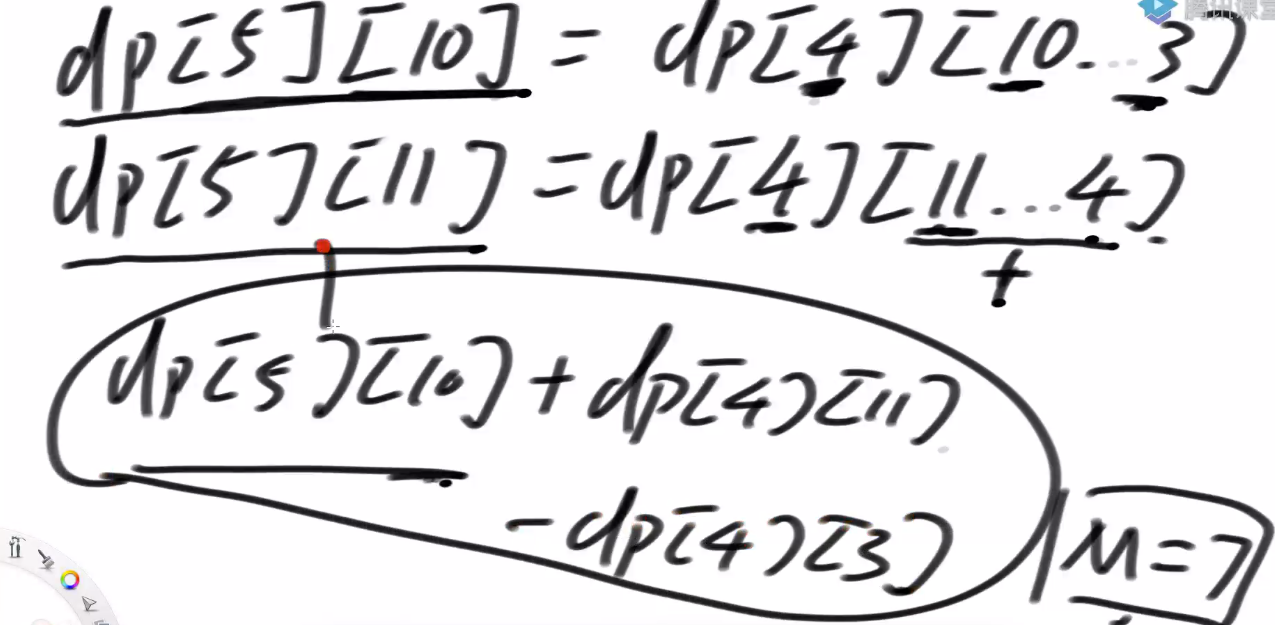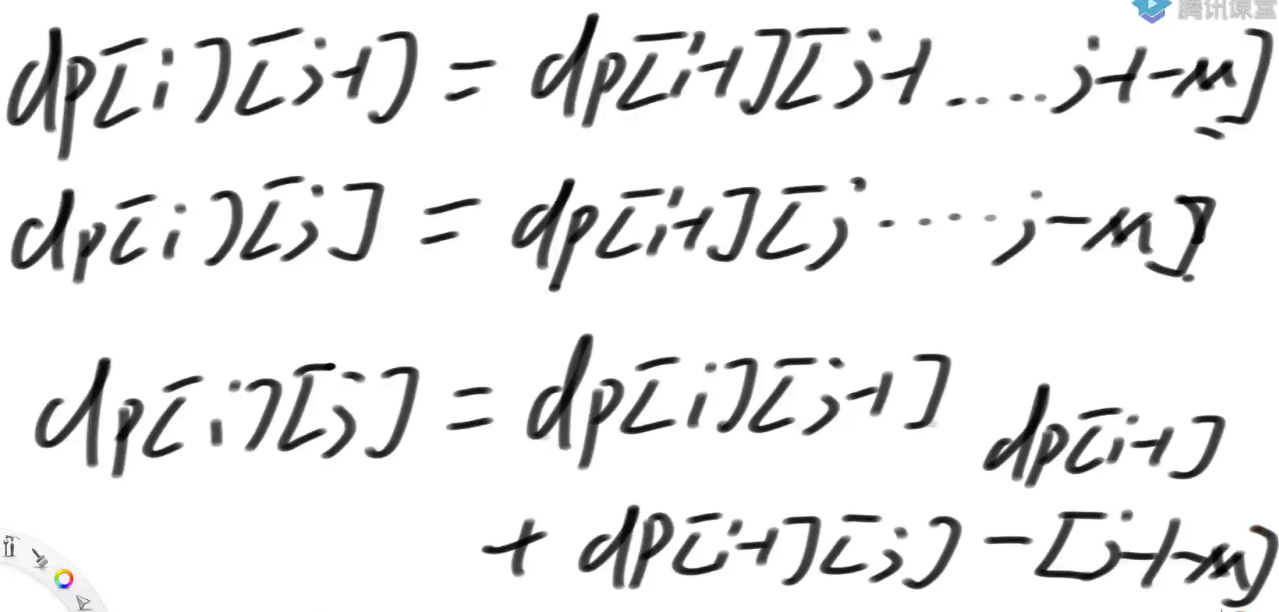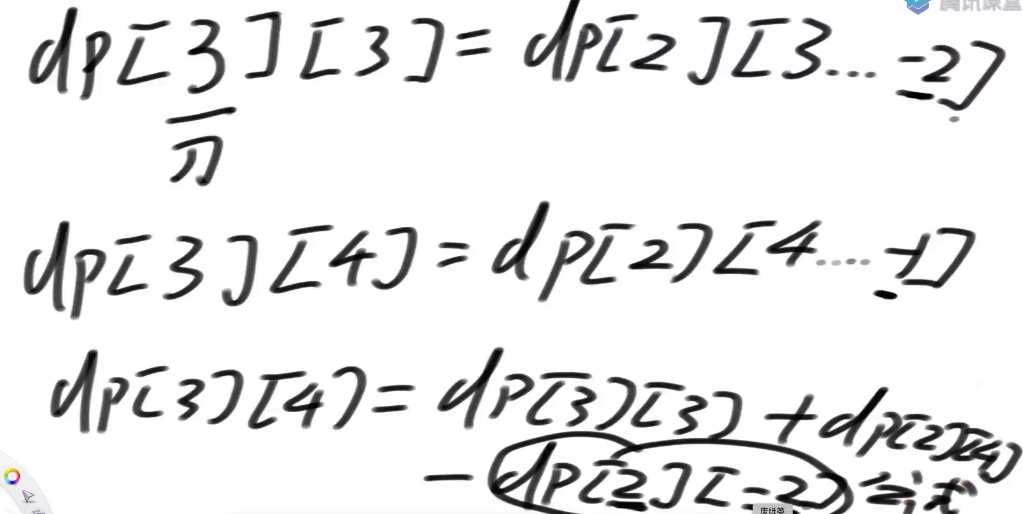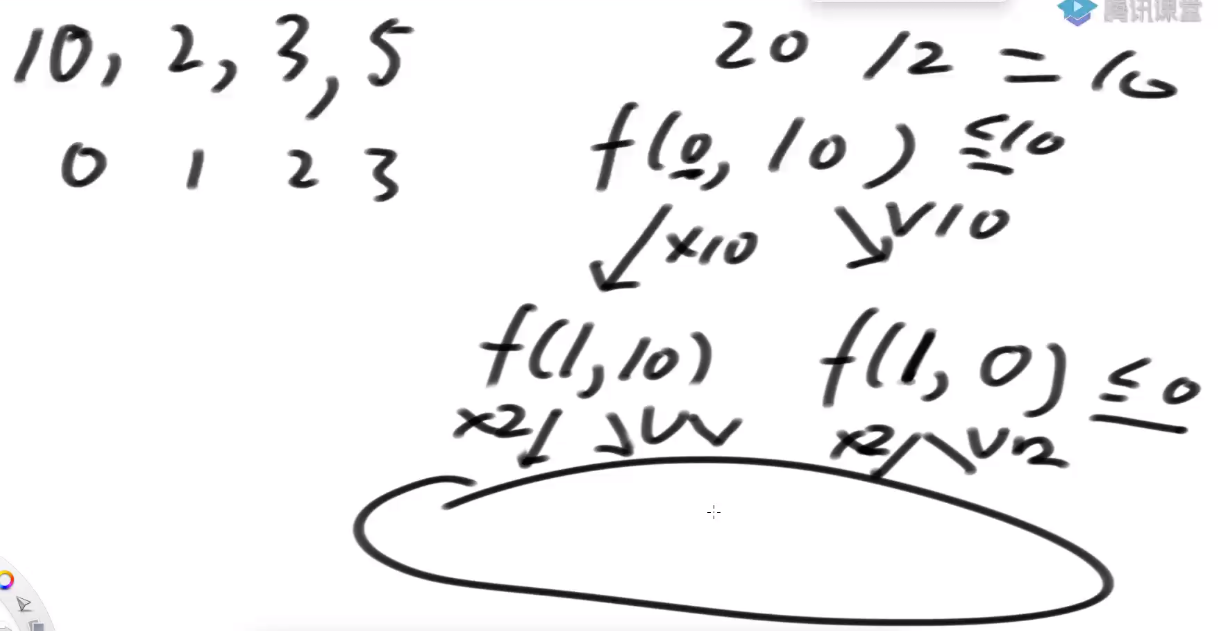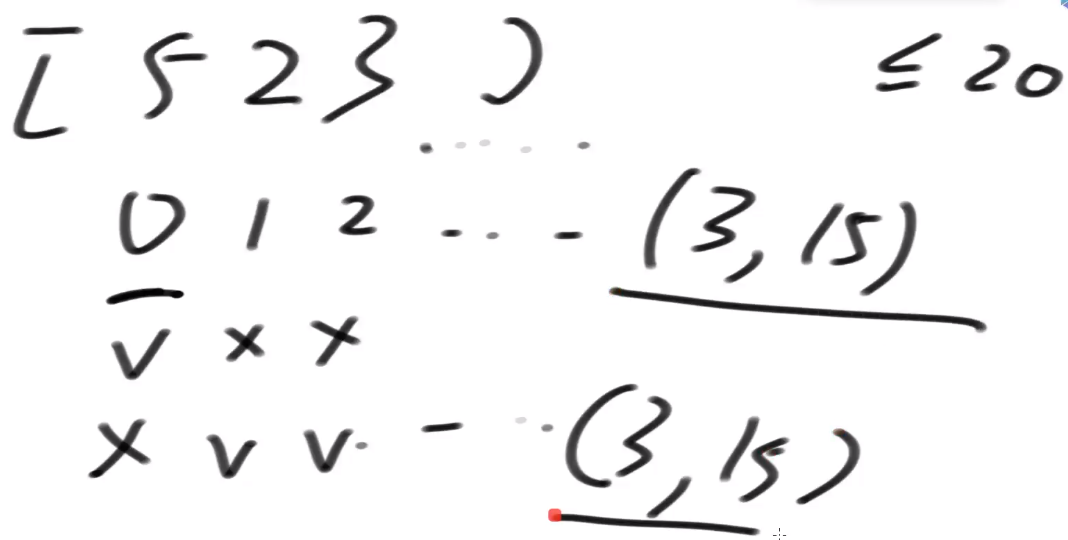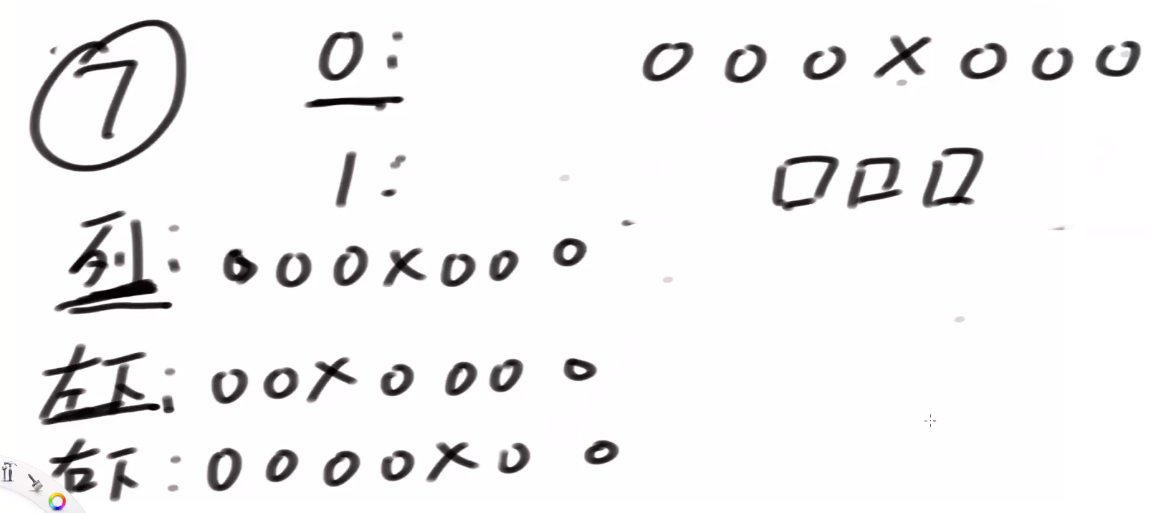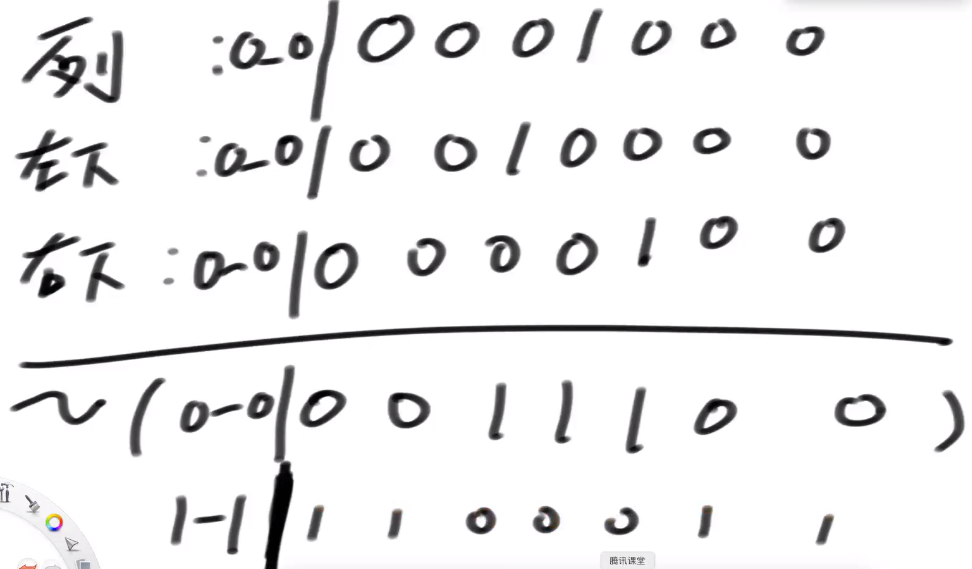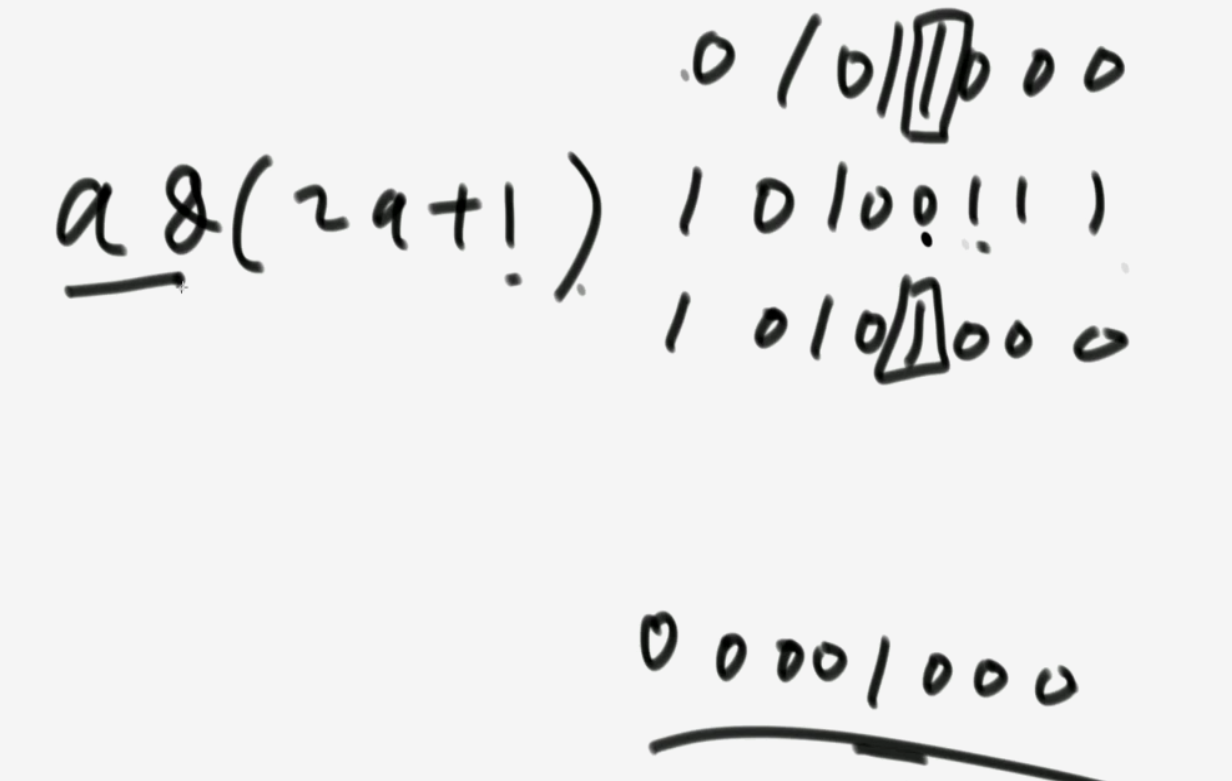从暴力递归到动态规划

暴力递归

1. 把问题转化为规模缩小了的同类问题的子问题
2. 有明确的不需要继续进行递归的条件（base case）
3. 有当得到了子问题的结果之后的决策过程
4. 不记录每一个子问题的解

汉诺塔问题

打印 n 层汉诺塔从最左边移动到最右边的全部过程

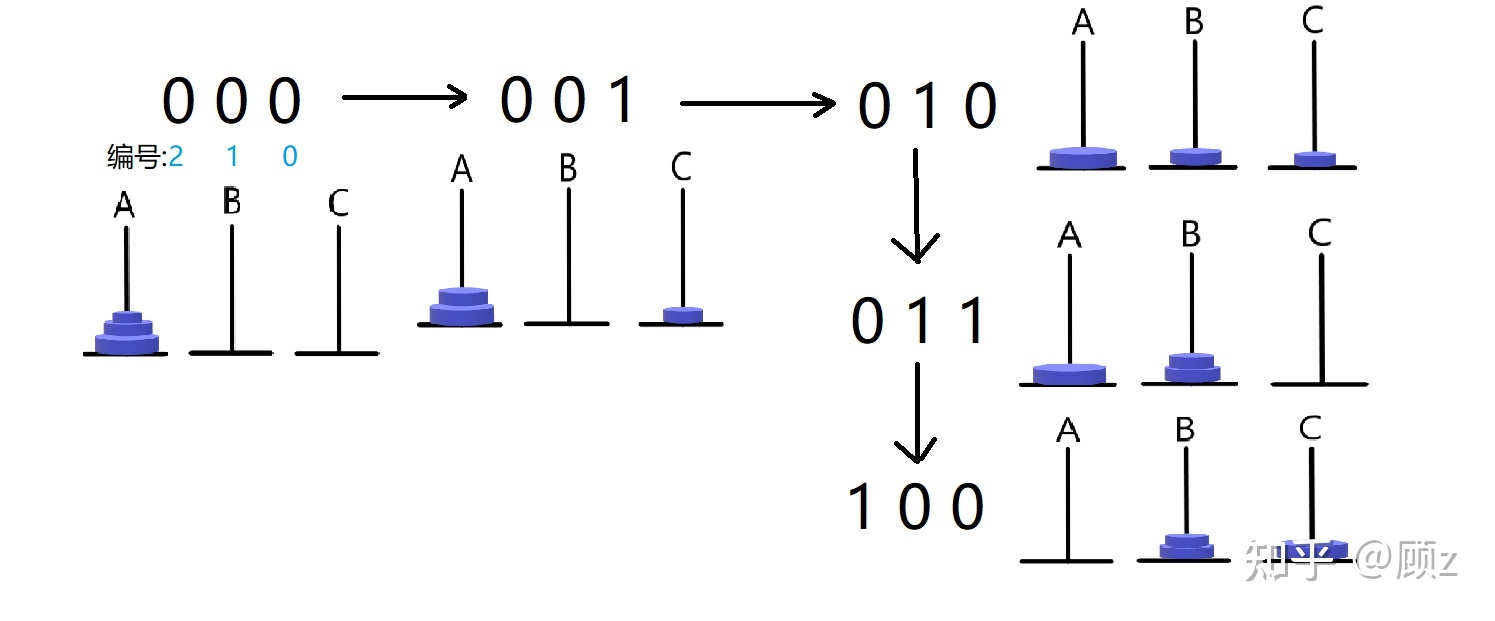
假设有 3 跟柱子，左、中、右，我们细分为如下三个步骤：

1. 将 1~N-1 层圆盘从左 -> 中（大问题，需要继续划分为小问题）

2. 将第 N 层圆盘从左 -> 右（base case）

3. 将 1~N-1 层圆盘从中 -> 右（大问题，需要继续划分为小问题）

完整流程

// 将left圆盘挪到right
	public static void leftToRight(int n) {
		// 只剩一个直接打印
		if (n == 1) {
			System.out.println("move 1 from left to right");
			return;
		}
		// 不止一个 先把上层的移动
		leftToMid(n - 1); // 从右移动到中间
		System.out.println("move " + n + " from left to right");
		midToRight(n - 1); // 从中间移动到右边
	}

	//左到中
	public static void leftToMid(int n) {
		if (n == 1) {
			System.out.println("move 1 from left to mid");
			return;
		}
		leftToRight(n - 1);
		System.out.println("move " + n + " from left to mid");
		rightToMid(n - 1);

	}

	//中到右
	public static void midToRight(int n) {
		if (n == 1) {
			System.out.println("move 1 mid to right");
			return;
		}
		midToLeft(n - 1);
		System.out.println("move " + n + " from mid to right");
		leftToRight(n - 1);

	}
	
	//中到左
	public static void midToLeft(int n) {
		if (n == 1) {
			System.out.println("move 1 from mid to left");
			return;
		}
		midToRight(n - 1);
		System.out.println("move " + n + " from mid to left");
		rightToLeft(n - 1);

	}
	
	
	//右到中
	public static void rightToMid(int n) {
		if (n == 1) {
			System.out.println("move 1 from right to mid");
			return;
		}
		rightToLeft(n - 1);
		System.out.println("move " + n + " from right to mid");
		leftToMid(n - 1);

	}
	
	
	//右到左
	public static void rightToLeft(int n) {
		if (n == 1) {
			System.out.println("move 1 from right to left");
			return;
		}
		rightToMid(n - 1);
		System.out.println("move " + n + " from right to left");
		midToRight(n - 1);

	}
	
	
	public static void hanoi1(int n) {
		leftToRight(n);
	}
	
	
	
	public static void main(String[] args) {
		int n=3;
		hanoi1(n);
		System.out.println("=======================");
	}

优化写法

通过上面完整流程我们可以发现 n 的规模不断减少，并且每次的交换都是从 from 到 to 而 other 传递给下一个使用。

	public static void f(int n, String from, String to, String other) {
		if (n == 1) {
			// 只剩一个直接移动 从 from 到 to
			System.out.println("move 1 from " + from + " to " + to);
		} else {
			// 不止一个 先把n-1从 当前位置移动到其他位置 
			f(n - 1, from, other, to);
			// 剩下n自己一个 直接 从 from 到 to
			System.out.println("move " + n + " from " + from + " to " + to);
			// 再把other的圆盘移动到
			f(n - 1, other, to, from);
		}
	}

	public static void main(String[] args) {
		int n = 3;
		if(n > 0) {
			f(n,"left","right","mid");
		}
		System.out.println("=======================");
		
	}

非递归使用栈实现

	public static class Record {
		public boolean finish1; 
		public int base;
		public String from;
		public String to;
		public String other;

		public Record(boolean f1, int b, String f, String t, String o) {
			finish1 = false;
			base = b;
			from = f;
			to = t;
			other = o;
		}
	}

		public static void hanoi3(int N) {
		if (N < 1) {
			return;
		}
		Stack<Record> stack = new Stack<>();
		stack.add(new Record(false, N, "left", "right", "mid"));
		while (!stack.isEmpty()) {
			Record cur = stack.pop();
			if (cur.base == 1) {
				System.out.println("Move 1 from " + cur.from + " to " + cur.to);
				if (!stack.isEmpty()) {
					stack.peek().finish1 = true;
				}
			} else {
				if (!cur.finish1) {
					stack.push(cur);
					stack.push(new Record(false, cur.base - 1, cur.from, cur.other, cur.to));
				} else {
					System.out.println("Move " + cur.base + " from " + cur.from + " to " + cur.to);
					stack.push(new Record(false, cur.base - 1, cur.other, cur.to, cur.from));
				}
			}
		}
	}

字符排列

字符串的全部子序列

从左往右依次尝试的模型

打印一个字符串的全部子序列，包括空字符串

• 需要保证字符的前后顺序
• “abc” =》a,b,c,ab,ac,bc,abc,null
• 暴力穷举

	/**
	 * 将字符串转为字符数组 调用process1
	 * @param s
	 * @return
	 */
	public static List<String> subs(String s){
		char[] str = s.toCharArray();
		String path ="";
		List<String> ans = new ArrayList<>();
		process1(str,0,ans,path);
		return ans;
		
	}
	/**
	 * 
	 * @param str 字符数组
	 * @param index 当前字符下标
	 * @param ans 结果集合
	 * @param path 当前子序列
	 */
	public static void process1(char[] str, int index, List<String> ans, String path) {
		//当前 index已经超过数组数量 
		if(index ==str.length) {
			ans.add(path);
			return;
		}
		//不要当前字符 path不变 index+1
		process1(str, index+1, ans, path);
		//要当前字符 path拼接当前字符 index+1
		process1(str, index+1, ans, path+String.valueOf(str[index]));
	}

字符串的全部子序列 不出现重复子序列

与全子序列相同 只是结果集合使用了 set 集合去重

	public static List<String> subsNoRepeat(String s) {
		char[] str = s.toCharArray();
		String path = "";
		//使用set集合去重
		HashSet<String> set = new HashSet<>(); 
		process2(str, 0, set, path);
		List<String> ans = new ArrayList<>();
		for (String cur : set) {
			ans.add(cur);
		}
		return ans;
	}
	
	
	public static void process2(char[] str, int index, HashSet<String> set, String path) {
		if (index == str.length) {
			set.add(path);
			return;
		}
		String no = path;
		process2(str, index + 1, set, no);
		String yes = path + String.valueOf(str[index]);
		process2(str, index + 1, set, yes);
	}

字符串的全排列

	public static List<String> permutation1(String s) {
		List<String> ans = new ArrayList<>();
		if (s == null || s.length() == 0) {
			return ans;
		}
		char[] str = s.toCharArray();
		// 可变集合 存放的是字符串的每个字符 方便移除和恢复
		ArrayList<Character> rest = new ArrayList<>();
		for (char c : str) {
			rest.add(c);
		}
		String path = "";
		f(rest, path, ans);
		return ans;

	}

	/**
	 * 
	 * @param rest 还剩哪些字符没有使用
	 * @param path 当前排列字符串
	 * @param ans  结果集合
	 */
	public static void f(ArrayList<Character> rest, String path, List<String> ans) {
		if (rest.isEmpty()) {
			ans.add(path);
			return;
		}
		int n = rest.size();
		for (int i = 0; i < n; i++) {
			char cur = rest.get(i);
			// 移除当前字符
			rest.remove(i);
			// 递归并使用该字符
			f(rest, path + cur, ans);
			// 恢复现场
			rest.add(i, cur);
		}
	}
	
	
	public static List<String> permutation2(String s){
		List<String> ans = new ArrayList<>();
		if (s == null || s.length() == 0) {
			return ans;
		}
		char[] str = s.toCharArray();
		g1(str, 0, ans);
		return ans;

	}

	/**
	 * 
	 * @param str 字符数组
	 * @param index 当前到哪个下标
	 * @param ans 结果集合
	 */
	public static void g1(char[] str, int index, List<String> ans) {
		if(index == str.length) {
			ans.add(String.valueOf(str));
			return;
		}
		for (int i = index; i <str.length; i++) {
			swap(str,index,i);
			g1(str,index+1,ans);
			swap(str,index,i);
		}
		
	}
	

	public static void swap(char[] str, int index, int i) {
			char temp = str[i];
			str[i] = str[index];
			str[index] = temp;
	}
	
		public static void main(String[] args) {
		String s = "acc";
		List<String> ans1 = permutation1(s);
		for (String str : ans1) {
			System.out.println(str);
		}
		System.out.println("=======");
		List<String> ans2 = permutation2(s);
		for (String str : ans2) {
			System.out.println(str);
		}
	}

字符串的全排列 不出现重复排列

即每个字符只能使用一次

	public static List<String> permutation3(String s) {
		List<String> ans = new ArrayList<>();
		if (s == null || s.length() == 0) {
			return ans;
		}
		char[] str = s.toCharArray();
		g2(str, 0, ans);
		return ans;
	}

	
	public static void g2(char[] str, int index, List<String> ans) {
		if(index == str.length) {
			ans.add(String.valueOf(str));
			return;
		}
		//用于标记字符是否被使用过
		boolean[] vis = new boolean[26];
		for (int i = index; i < str.length; i++) {
			int cur = str[i] -'a';
			//当前字符没被使用过
			if(!vis[cur]) {
				vis[cur] = true;
				swap(str, index, i);
				g2(str, index+1, ans);
				swap(str, index, i);
			}
			
		}
	}
	

	public static void swap(char[] str, int index, int i) {
			char temp = str[i];
			str[i] = str[index];
			str[index] = temp;
	}


		public static void main(String[] args) {
		String s = "acc";
		System.out.println("=======");
		List<String> ans3 = permutation3(s);
		for (String str : ans3) {
			System.out.println(str);
		}
	}

逆序一个栈 仅使用递归

给定一个栈，请逆序这个栈，不能申请额外的数据结构，只能使用递归函数

1. 移除并缓存栈顶
2. 判断栈是否为空 即判断是否为栈底
3. 如不为空 递归自身
4. 等递归 base case 触发 回将当前递归方法中的缓存栈顶重新入栈 即把栈底提取出来 并把保持栈的顺序
5. 创建一个新的 g 递归方法 用于调用上面的提取栈底方法 然后调用自身 g 方法 等 g 递归函数 base case 触发 将提取栈底方法返回的值 入栈压栈底 不断重复此时完成栈的反转

	public static void g(Stack<Integer> stack) {
		if(stack.isEmpty()) {
			//g函数的base case
			return; 
		}
		// 获取栈底元素
		int bottom = f(stack);
		// 递归g方法
		g(stack);
		// 等待g函数的base case触发即递归结束 则将提取的栈底元素 重新压栈
		stack.push(bottom);
		
	}
	
	public static int f(Stack<Integer> stack) {
		// 移除并缓存当前栈顶
		int result = stack.pop();
		// 判断栈是否为空
		if(stack.isEmpty()) {
			// 栈为空 当前为栈底 直接返回
			return result;
		 } else {
			 // last为缓存的栈底
			 int last = f(stack);
			 // 不是栈底的 重新入栈 防止一次返回多个栈底
			 stack.push(result);
			 return last;
		 }
		
	}
	
	public static void main(String[] args) {
		Stack<Integer> test = new Stack<Integer>();
		test.push(1);
		test.push(2);
		test.push(3);
		test.push(4);
		test.push(5);
		g(test);
		while (!test.isEmpty()) {
			System.out.println(test.pop());
		}
	}

动态规划

动态规划算法是通过拆分问题，定义问题状态和状态之间的关系，使得问题能够以递推（或者说分治）的方式去解决，是暴力递归的优化版本。

1. 从暴力递归中来
2. 将每一个子问题的解记录下来，避免重复计算
3. 把暴力递归的过程，抽象成了状态表达
4. 并且存在化简状态表达，使其更加简洁的可能

接着我们明确一般的解答流程：暴力递归解法 -> 带记忆数组的递归解法 ->(非递归) 动态规划解法，只要按照这个流程去做基本都能解答出来。

斐波那契数列

斐波那契数列的递推式是 f (n)=f (n-1)+f (n-2)。(1,1,2,3,5,8...)

暴力递归

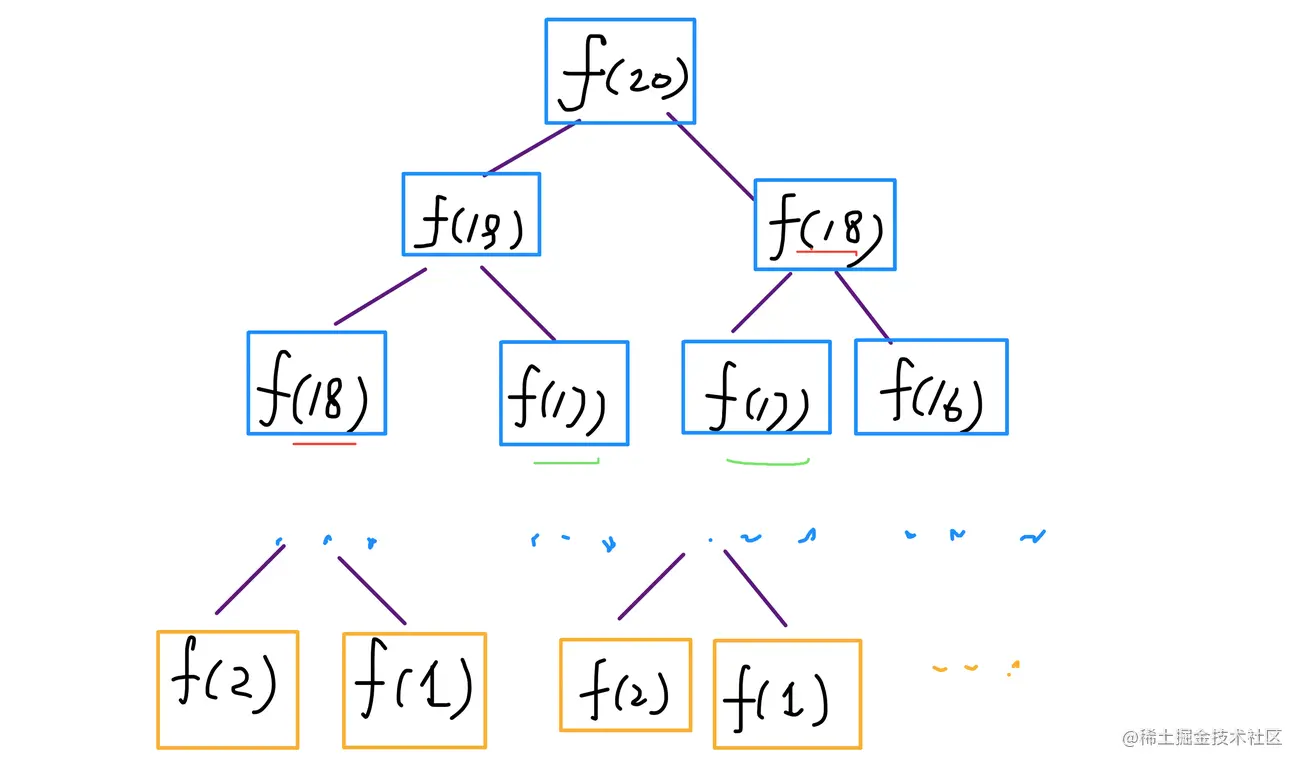
暴力递归之所以低效是因为存在大量的重复计算，借鉴 LeetCode 题解区一位大佬的图 (opens new window)，如图所示，f (20)=f (19)+f (18)，而 f (19)=f (18)+f (17)，这里就产生了重复计算，而且这种重复计算还很多，正是因为这些大量的重复计算，所以暴力递归很低效，这个算法的时间复杂度为 O (2^n)。

	public static int f1(int n) {
		if(n==1 || n==2) {
			return 1;
		}
		 return f1(n-1)+f1(n-2);
	}
	
	
	public static void main(String[] args) {
		System.out.println(f1(8));
	}

记忆搜索

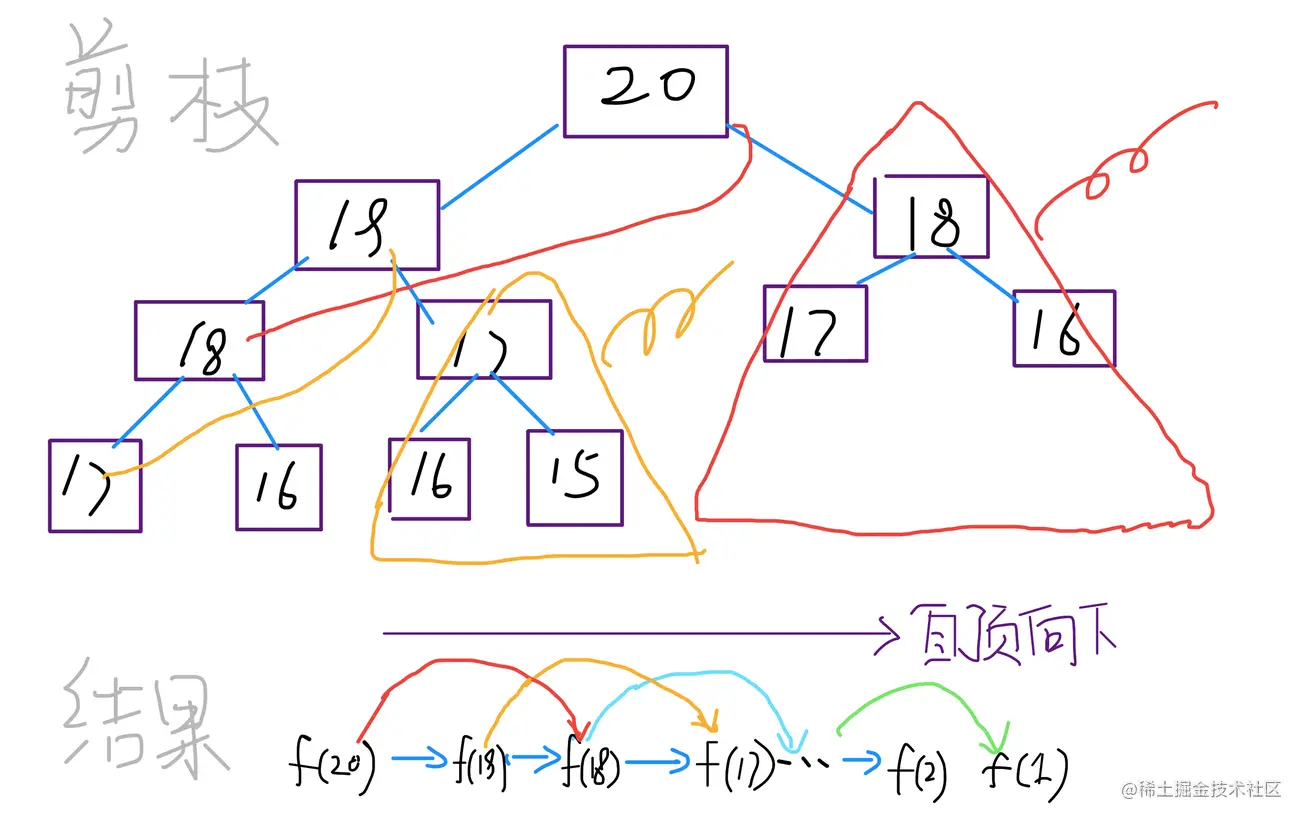
步骤一的计算过程中国充斥着大量的重复计算，解决重复计算的方法很简单，用一个数组或者其他容器装起来，递归的时候判断是否已经计算过的，如果已经计算过，就直接返回。这个是典型的用过空间换时间的做法，反应到上述递归图中就是 “剪枝” 了。

f (20)，可看到每个分支都存在大量重复计算，如果我们能够把这些计算过的值先保存下来，是不是就可以避免了重复计算，这就是带有备忘录的递归解法，这也是动态规划的第一个性质：重叠子问题。

/**
	 * 
	 * @param n 求第几项
	 * @param memo 缓存表
	 * @return
	 */
	public static int helper(int n, int[] memo) {
		if(n==1 || n==2) {
			return 1;
		}
		
		//当缓存第n项不为0 则说明之前算过值 直接返回缓存表的值
		if(memo[n] != 0) {
			return memo[n];
		}
		
		//没有被算过
		memo[n] = helper(n-1, memo) + helper(n-2, memo);
		return memo[n];
	}


	public static void main(String[] args) {
		System.out.println(f2(8));
		
	}

动态规划

写出来了带记忆数组的递归解法，动态规划也就基本成型了，因为这两者区别不是很大，前者是自顶向下的，后者是自底向上的。自顶向下的意思是，比如求 f (5)，递归的做法是先递归到 f (1)，然后再往上走得到 f (5)；而动态规划是直接从 f (1) 开始往上求的。

	public static int f3(int n) {
		int[] dp = new int[n+1];
		dp[1] = dp[2] = 1;
		for (int i = 3; i < dp.length; i++) {
			dp[i] = dp[i-1] + dp[i-2];
		}
		return dp[n];
	}


	public static void main(String[] args) {
		int n = 8;
		System.out.println(f3(n));
		
	}

总结

带记忆数组的递归和动态规划相似，他两的时间复杂度也相差无几，动态规划中很关键的转移方程就是从暴力递归中而来的，所以当遇到没做过或者不能一下子写出转移方程的，从暴力递归做起总是一个正确的选择。

机器人行走

假设有排成一行的N个位置记为1~N，N一定大于或等于2
开始时机器人在其中的M位置上(M一定是1~N中的一个)
如果机器人来到1位置，那么下一步只能往右来到2位置；
如果机器人来到N位置，那么下一步只能往左来到N-1位置；
如果机器人来到中间位置，那么下一步可以往左走或者往右走；
规定机器人必须走K步，最终能来到P位置(P也是1~N中的一个)的方法有多少种
给定四个参数 N、M、K、P，返回方法数

暴力递归

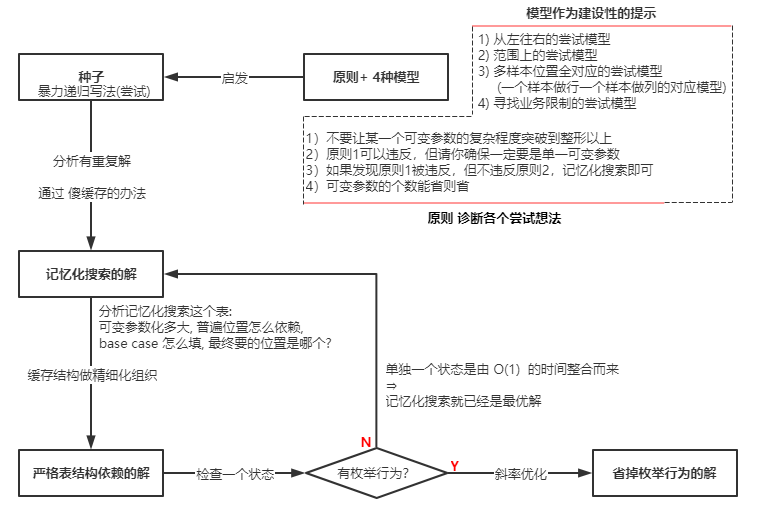
暴力尝试（回溯）优化成动态规划的步骤：

1. 写出暴力尝试版本
2. 转换成记忆化搜索（基础动态规划版本）
3. 根据 base case 和调用过程画表，转换成动态规划。
4. 优化动态规划。如斜率优化。

/**
	 * 
	 * @param n     1~N 个位置
	 * @param start 从哪个位置开始
	 * @param aim   目标位置
	 * @param k     要走多少步
	 * @return
	 */
	public static int ways1(int n, int start, int aim, int k) {
		if (n < 2 || start < 1 || start > n || aim < 1 || aim > n || k < 1) {
			return -1;
		}
		return process1(start, k, aim, n);
	}

	/**
	 * 
	 * @param cur  当前机器人在什么位置
	 * @param rest 还剩下多少步要走
	 * @param aim  目标位置
	 * @param n    有 1~n的位置
	 * @return
	 */
	public static int process1(int cur, int rest, int aim, int n) {
		// 当前步数已走完
		if (rest == 0) {
			// 当前位置是否为目标 是则返回方法数+1 否则返回0
			return cur == aim ? 1 : 0;
		}

		// 当前在1位置 只能往右(前)走
		if (cur == 1) {
			return process1(2, rest - 1, aim, n);
		}

		// 当前在n位置 只能往左(后)走
		if (cur == n) {
			return process1(cur - 1, rest - 1, aim, n);
		}

		// 左右都可以走
		return process1(cur - 1, rest - 1, aim, n) + process1(cur + 1, rest - 1, aim, n);

	}

	public static void main(String[] args) {
		System.out.println(ways1(5, 2, 4, 6));
	}

记忆缓存法

自顶向下动态规划又称记忆化搜索 上述方法求解时 多次反复求剩余 k-x 步数时 n-x 位置的值 我们可以通过一张二维表来存储 剩余 k 部时 n 位置的值

n 和 aim 是固定参数，每次调用都不会变，而 cur 和 k 每次调用过程都会变，因此 ways1 函数的调用结果取决于 start 和 k 的值，我们只要用一个二维表来记录每个调用过程的返回值便能大大提高效率，这种方法叫做记忆缓存法。

public static int ways2(int n, int start, int aim, int k) {
		if (n < 2 || start < 1 || start > n || aim < 1 || aim > n || k < 1) {
			return -1;
		}
		// dp为缓存表 dp[cur][rest] == -1 说明 process1(cur,rest)之前没有算过
		// dp[cur][rest] != -1 说明 process1(cur,rest)之前算过
		int[][] dp = new int[n + 1][k + 1];
		// 初始化为-1
		for (int i = 0; i <= n; i++) {
			for (int j = 0; j <= k; j++) {
				dp[i][j] = -1;
			}
		}

		return process2(start, k, aim, n, dp);
	}

	/**
	 * 
	 * @param cur  当前位置
	 * @param rest 剩余步数
	 * @param aim  目标
	 * @param n    1~n位置
	 * @param dp   缓存表
	 * @return
	 */
	public static int process2(int cur, int rest, int aim, int n, int[][] dp) {
		if (dp[cur][rest] != -1) {
			// 之前有求过 直接返回
			return dp[cur][rest];
		}

		// 之前没有算过的
		int ans = 0;
		if (rest == 0) {
			ans = cur == aim ? 1 : 0;
		} else if (cur == 1) {
			ans = process2(2, rest - 1, aim, n, dp);
		} else if (cur == n) {
			ans = process2(n - 1, rest - 1, aim, n, dp);
		} else {
			ans = process2(cur - 1, rest - 1, aim, n, dp) + process2(cur + 1, rest - 1, aim, n, dp);
		}
		// 将当前算的值记录到缓存表中
		dp[cur][rest] = ans;
		return ans;

	}

	public static void main(String[] args) {
		System.out.println(ways2(5, 2, 4, 6));
	}

动态规划

通过具体情况画表分析发现规律

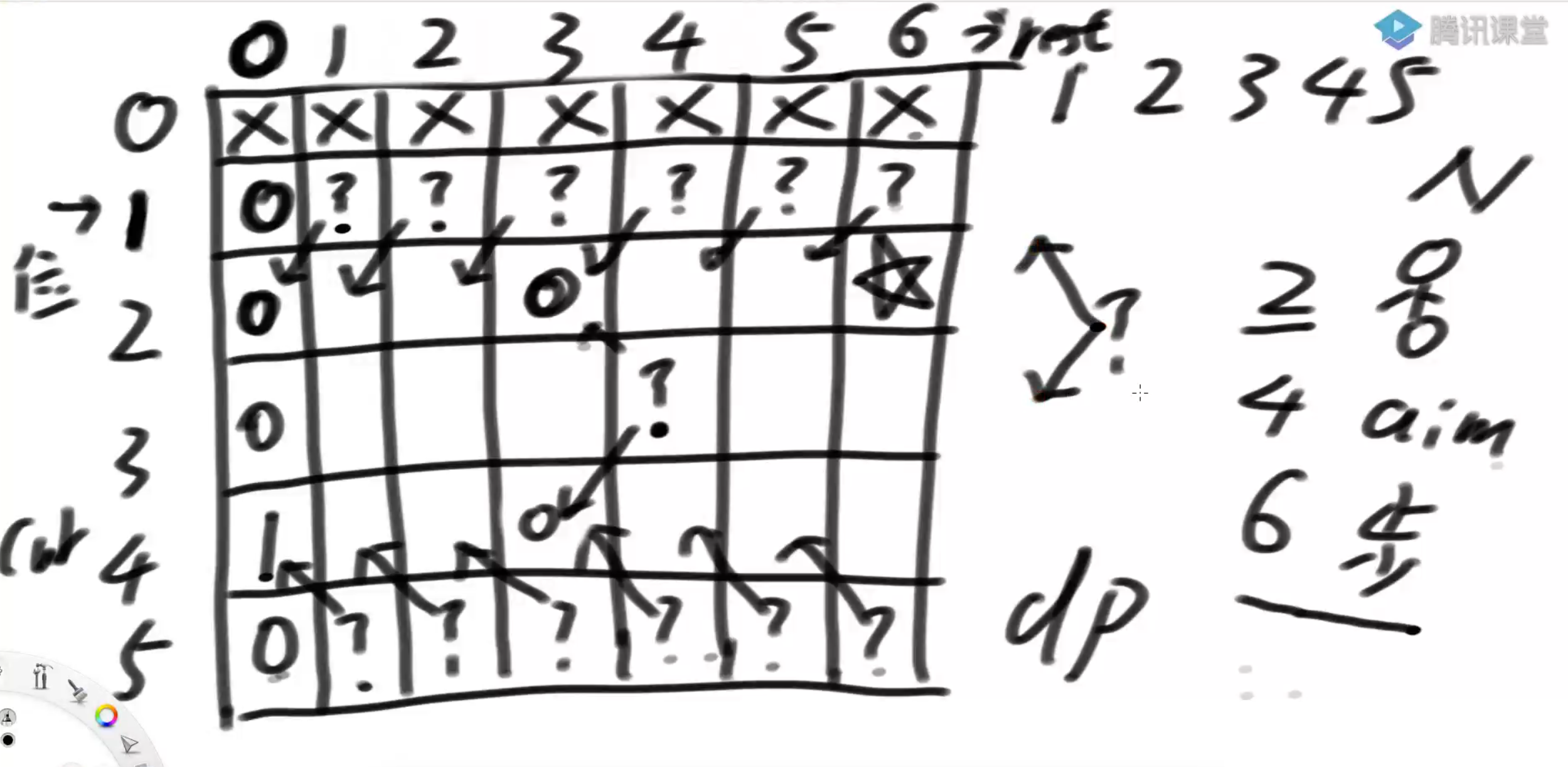
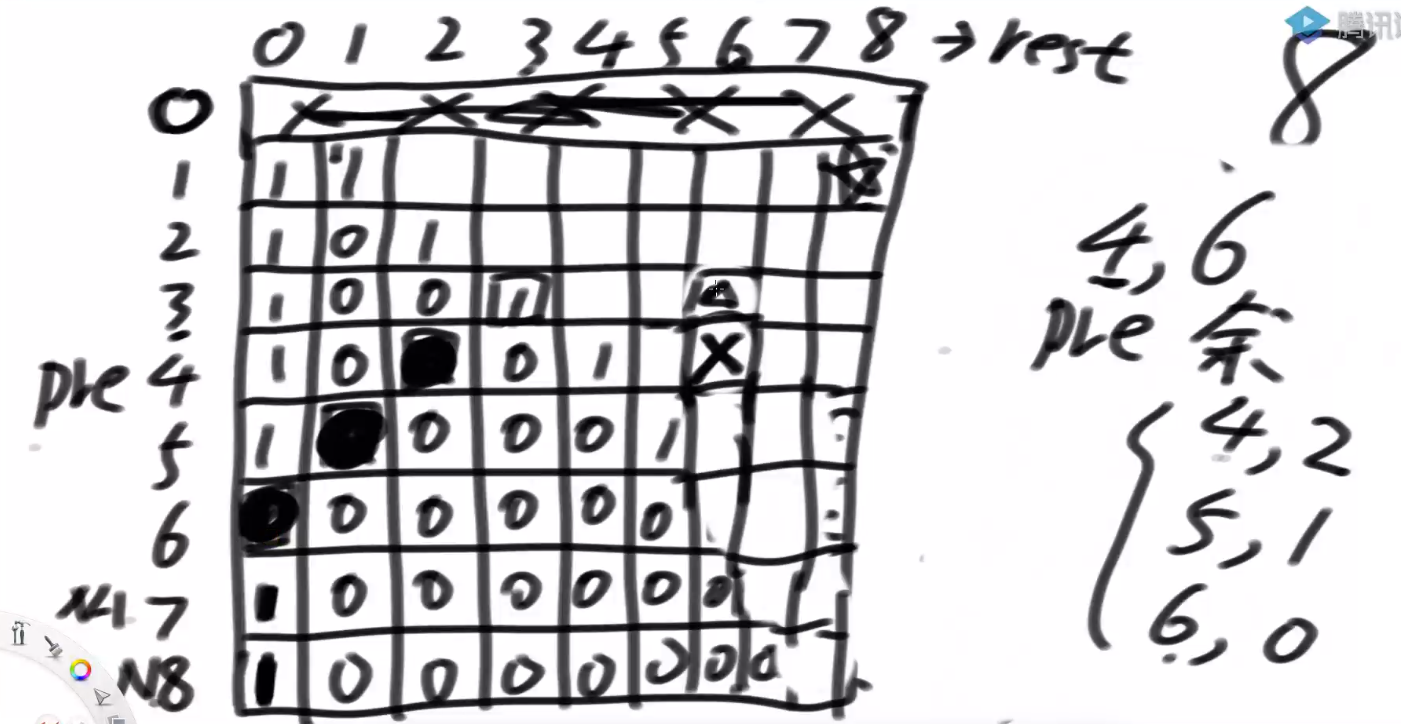
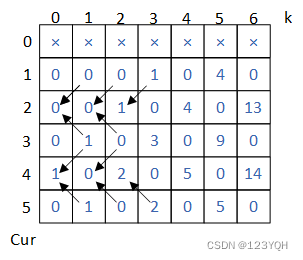
测试用例：n = 5, cur = 4, aim = 6, k = 6。

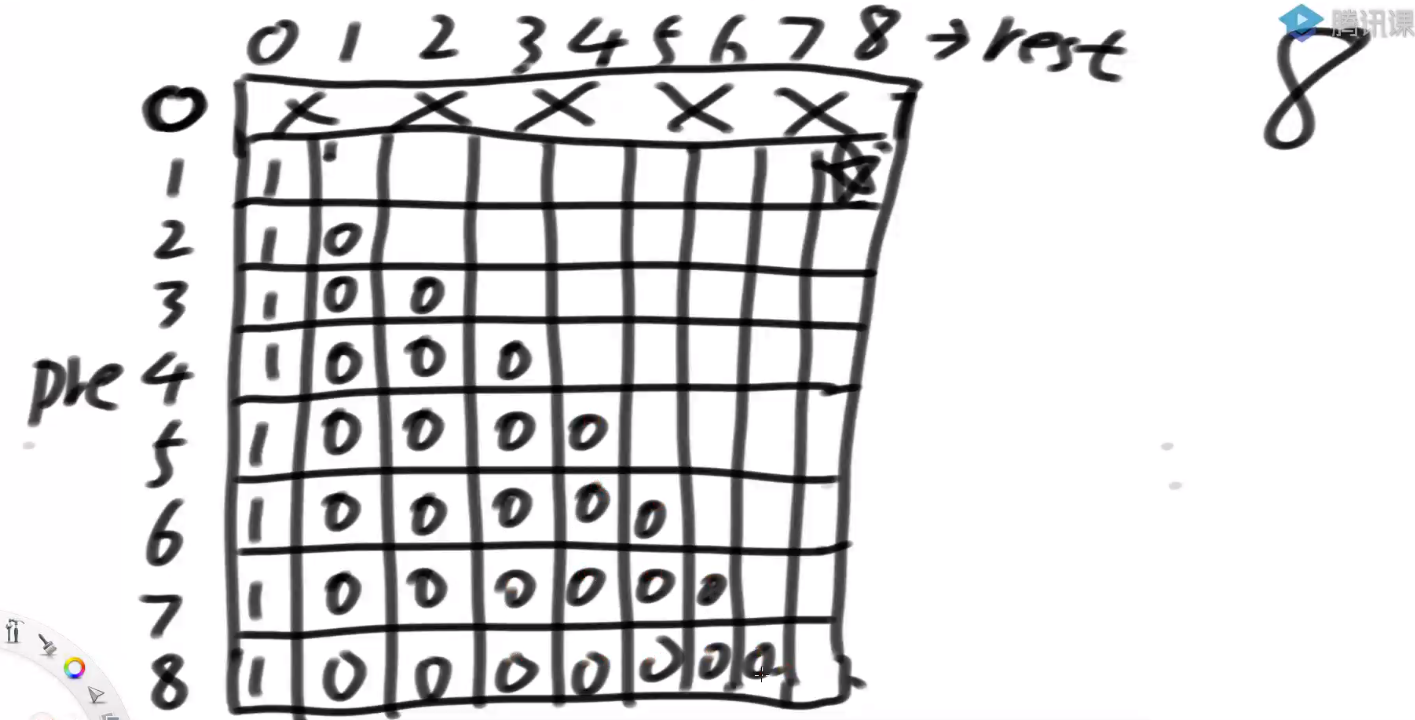
由于 n = 5，cur 的变化范围为 1~5，k = 6，k 的变化范围为 0~6，我们可以画出一个 6×7 的二维表。

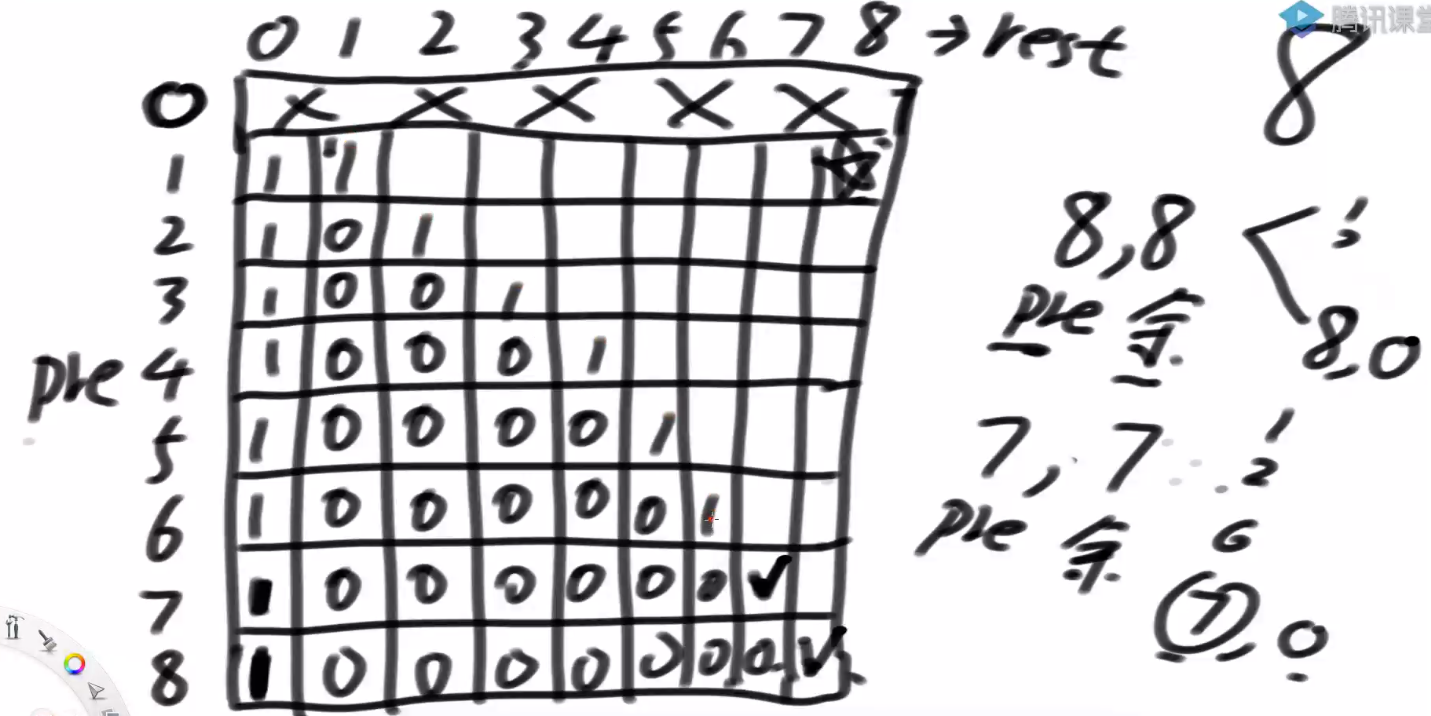
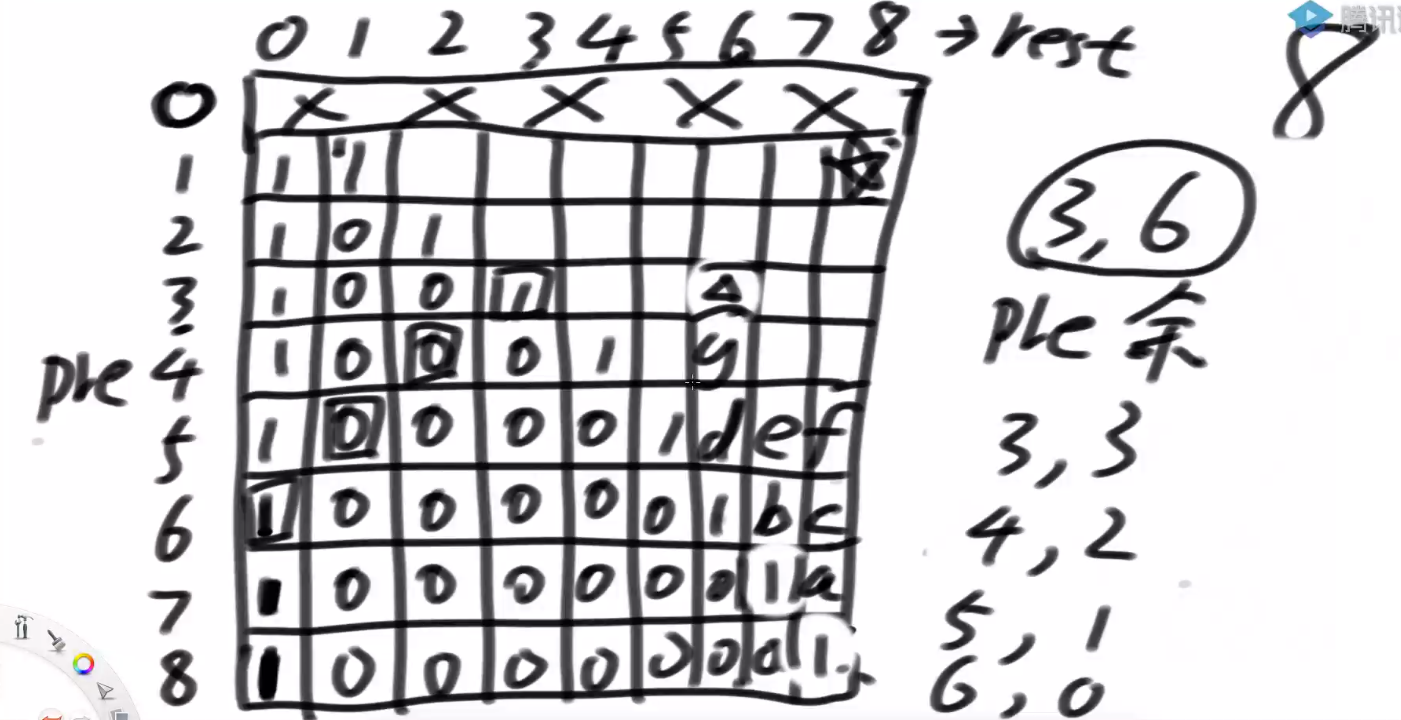
看 base case：由于 cur 的变化范围为 1~5 不能为 0，所以 cur=0 这一行打上 ×。k = 0 时，cur==aim 的时候才为 1，其他时候为 0。

当 cur==1 时，每一行依赖左下这一行；当 cur=5 时，每一行依赖左上一行；当普遍位置时，每一格依赖左上和左下两格相加。

public static int ways3(int n, int start, int aim, int k) {
		if (n < 2 || start < 1 || start > n || aim < 1 || aim > n || k < 1) {
			return -1;
		}
		int[][] dp = new int[n + 1][k + 1];
		// 目标位置 剩余0步 肯定为1次方法
		dp[aim][0] = 1;
		for (int rest = 1; rest <= k; rest++) {
			// 向右走的情况 当前位置 在1位置 剩余步数 = 在2位置 剩余步数-1的值
			dp[1][rest] = dp[2][rest - 1];
			for (int cur = 2; cur < n; cur++) {
				// 左右都可以走的情况 当前位置剩余步数的值 依赖于dp[cur-1][rest-1] 和 dp[cur+1][rest-1]
				dp[cur][rest] = dp[cur - 1][rest - 1] + dp[cur + 1][rest - 1];
			}
			// 向左走的情况 当前位置 在n位置 剩余步数 = 在n-1位置 剩余步数-1的值
			dp[n][rest] = dp[n - 1][rest - 1];
		}
		// 直接返回开始位置 多少步的值
		return dp[start][k];

	}

	public static void main(String[] args) {
		System.out.println(ways3(5, 2, 4, 6));
	}

抽纸牌

给定一个整型数组arr，代表数值不同的纸牌排成一条线
玩家A和玩家B依次拿走每张纸牌
规定玩家A先拿，玩家B后拿
但是每个玩家每次只能拿走最左或最右的纸牌
玩家A和玩家B都绝顶聪明
请返回最后获胜者的分数 即得分最高分数

题目：给定一个整型数组arr，代表数值不同的纸牌排成一条线。玩家A和玩家B依次拿走每张纸牌，规定玩家A先拿，玩家B后拿，但是每个玩家每次只能拿走最左或最右的纸牌，玩家A和玩家B都绝顶聪明。请返回最后获胜者的分数。
【举例】
arr=[1,2,100,4]。
开始时，玩家A只能拿走1或4。如果开始时玩家A拿走1，则排列变为[2,100,4]，接下来玩家B可以拿走2或4，然后继续轮到玩家A...
如果开始时玩家A拿走4，则排列变为[1,2,100]，接下来玩家B可以拿走1或100，然后继续轮到玩家A...
玩家A作为绝顶聪明的人不会先拿4，因为拿4之后，玩家B将拿走100。所以玩家A会先拿1，让排列变为[2,100,4]，接下来玩家B不管怎么选，100都会被玩家A拿走。玩家A会获胜，分数为101。所以返回101。
arr=[1,100,2]。
开始时，玩家A不管拿1还是2，玩家B作为绝顶聪明的人，都会把100拿走。玩家B会获胜，分数为100。所以返回100。

博弈论：双方玩家都不会在对方单独改变策略的情况下让对方获得最大收益

暴力递归

	public static int win1(int[] arr) {
		if (arr == null || arr.length == 0) {
			return 0;
		}
		// 先手获得的总卡牌数值
		int first = f1(arr, 0, arr.length - 1);
		// 后手获得的总卡牌数值
		int second = g1(arr, 0, arr.length - 1);
		// 返回最大数值 为赢家
		return Math.max(first, second);
	}

	/**
	 * 先手从arr[l~r]中获得最好分数返回
	 * 
	 * @param arr 卡牌数值
	 * @param l 左边卡牌开始位置
	 * @param r 右边卡牌开始位置
	 * @return
	 */
	public static int f1(int[] arr, int l, int r) {
		// 只剩一张牌 先手取走
		if (l == r) {
			return arr[l];
		}
		// 如果先手拿的是左边的牌，那么后手只能在[L+1,R]上拿牌
		int p1 = arr[l] + g1(arr, l + 1, r);
		// 如果先手拿的是右边的牌，那么后手只能在[L,R-1]上拿牌
		int p2 = arr[r] + g1(arr, l, r - 1);
		// 这两种情况下，先手肯定会只选择对自己最有利的方式，也就是返回最大值
		return Math.max(p1, p2);

	}
	
	//后手从arr[l-r] 获得最好的分数返回
	public static int g1(int[] arr, int l, int r) {
		// 如果只剩下一张牌了，又是后手，那就没牌拿
		if (l == r) {
			return 0;
		}
		// 先手拿走了l位置的数
		int p1 = f1(arr, l + 1, r);
		// 先手拿走了r位置的数
		int p2 = f1(arr, l, r - 1);
		// 因为是后手，所以没得选，只能选得分最少的方式
		// 得分多的方式被先手给选了
		return Math.min(p1, p2);
	}

	public static void main(String[] args) {
		int[] arr = { 5, 7, 4, 5, 8, 1, 6, 0, 3, 4, 6, 1, 7 };
		System.out.println(win1(arr));
	}

简单缓存

输入为f1(arr,0,7)

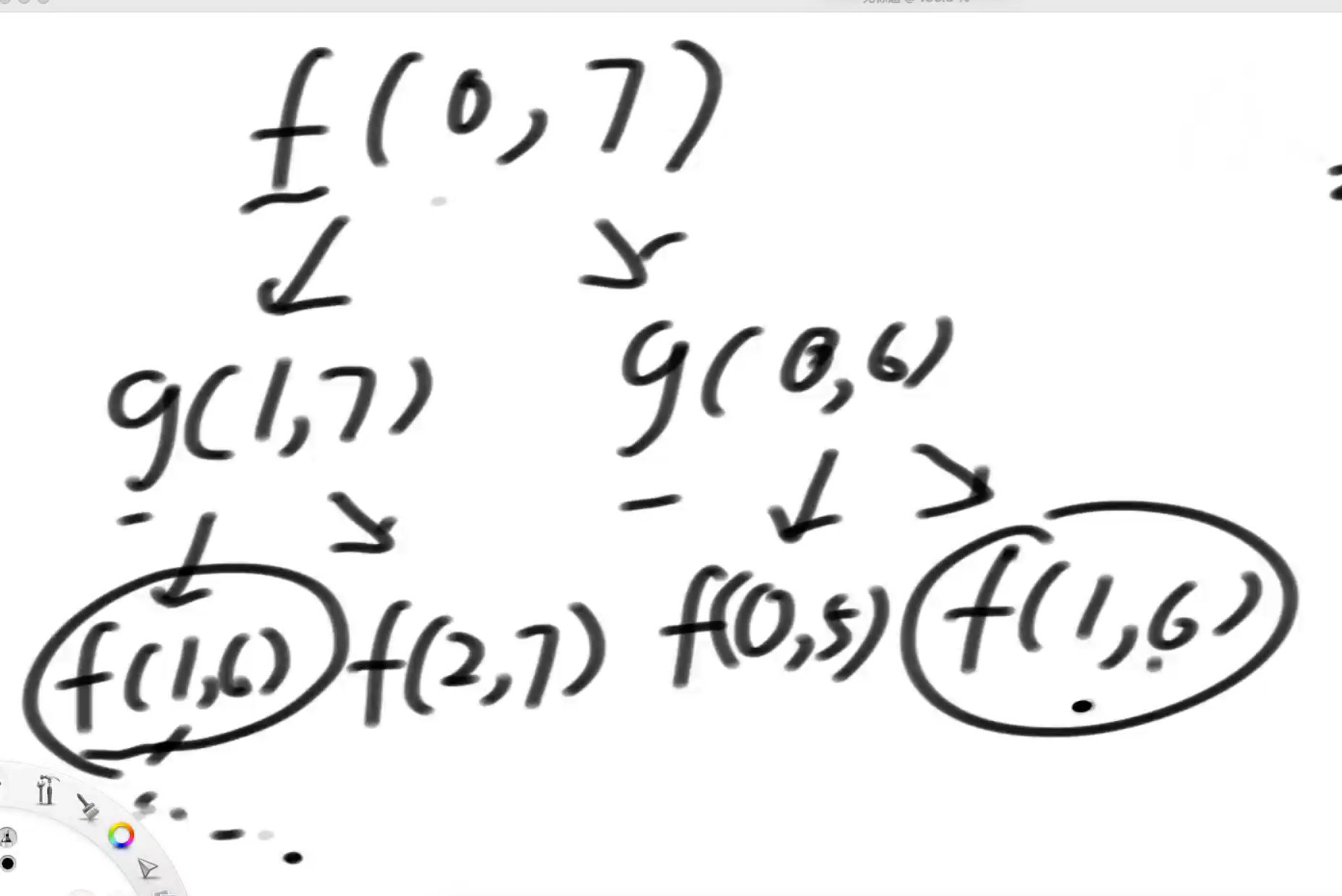
发现 f (1,6) 重复算了 并且可变参数为 l 和 r 可以使用缓存

	public static int win2(int[] arr) {
		if (arr == null || arr.length == 0) {
			return 0;
		}
		int n = arr.length;
		// 先手缓存表
		int[][] fmap = new int[n][n];
		// 后手缓存表
		int[][] gmap = new int[n][n];
		for (int i = 0; i < n; i++) {
			for (int j = 0; j < n; j++) {
				// 初始化为-1
				fmap[i][j] = gmap[i][j] = -1;
			}
		}
		int first = f2(arr, 0, arr.length - 1, fmap, gmap);
		int second = g2(arr, 0, arr.length - 1, fmap, gmap);
		return Math.max(first, second);
	}

	// 先手从arr[l~r]中获得最好分数返回
	public static int f2(int[] arr, int l, int r, int[][] fmap, int[][] gmap) {
		if (fmap[l][r] != -1) {
			return fmap[l][r];
		}
		int ans = 0;
		if (l == r) {
			ans = arr[l];
		} else {
			int p1 = arr[l] + g2(arr, l + 1, r, fmap, gmap);
			int p2 = arr[r] + g2(arr, l, r - 1, fmap, gmap);
			ans = Math.max(p1, p2);
		}
		fmap[l][r] = ans;

		return ans;

	}

	// 后手从arr[l-r] 获得最好的分数返回
	public static int g2(int[] arr, int l, int r, int[][] fmap, int[][] gmap) {
		if (gmap[l][r] != -1) {
			return gmap[l][r];
		}
		int ans = 0;
		if (l != r) {
			int p1 = f2(arr, l + 1, r, fmap, gmap);
			int p2 = f2(arr, l, r - 1, fmap, gmap);
			ans = Math.min(p1, p2);
		}
		gmap[l][r] = ans;

		return ans;
	}

	public static void main(String[] args) {
		int[] arr = { 5, 7, 4, 5, 8, 1, 6, 0, 3, 4, 6, 1, 7 };
		System.out.println(win2(arr));
	}

动态规划

输入样例arr=[7,4,16,15,1]

通过分析 f 函数的 base case 方向 f 表中的对角线为 arr [l]

// 只剩一张牌 先手取走
if (l == r) {
    return arr[l];
}

得出以下 f 表 l 不可能＜ r 所以左下角无值

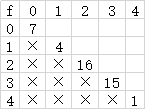
再分析 g 函数的 base case 发现 g 表的对角全为 0

// 如果只剩下一张牌了，又是后手，那就没牌拿
if (l == r) {
    return 0;
}

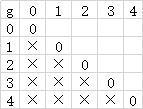
再分析其他格子的情况 通过 f 函数 我们发现 f 表剩下的格子是依赖于 g 表的 g[l+1][r] 和 g[l][r-1] 值 无法直接得出值 我们去分析 g 表

// 如果先手拿的是左边的牌，那么后手只能在[L+1,R]上拿牌
int p1 = arr[l] + g1(arr, l + 1, r);
// 如果先手拿的是右边的牌，那么后手只能在[L,R-1]上拿牌
int p2 = arr[r] + g1(arr, l, r - 1);

通过分析 g 函数 发现 g 表是依赖于 f 表中的 f[l+1][r] 和 f[l][r-1] 的最小值

// 先手拿走了l位置的数
int p1 = f1(arr, l + 1, r);
// 先手拿走了r位置的数
int p2 = f1(arr, l, r - 1);
// 因为是后手，所以没得选，只能选得分最少的方式
// 得分多的方式被先手给选了
return Math.min(p1, p2);

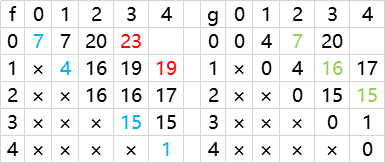
得出 g 表 g[0][1] 通过 f[0][1] 的左上和左下两的最小值得出 即蓝色标注的两数的最小值得出 g 表中红色位置的数

红色为得出的值 蓝色为 f 表依赖项 绿色为 g 表依赖

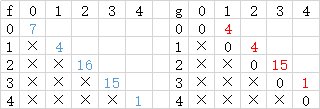
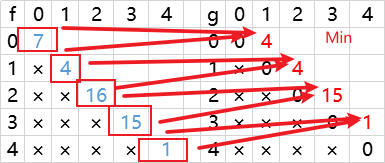
7和4 最小为 4
4和16 最小值 4
16和15 最小值 15
15和1 最小值 1

而 f 表又是依赖于 g 表的 通过 g 表反推 f 表的值

// 如果先手拿的是左边的牌，那么后手只能在[L+1,R]上拿牌
int p1 = arr[l] + g1(arr, l + 1, r);
// 如果先手拿的是右边的牌，那么后手只能在[L,R-1]上拿牌
int p2 = arr[r] + g1(arr, l, r - 1);
return Math.max(p1, p2);

案例如下:

int p1 = arr[0]+g[0+1][1];  //p1 = 7 + 0 
int p2 = arr[1]+g[0][1-1];  //p2 = 4 + 0
return Math.max(p1, p2);
//得出f[0][1] = 7

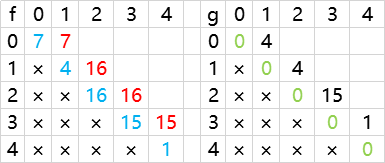
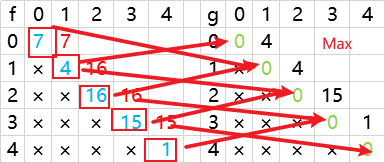
7+0=7
4+0=4
max = 7

4+0=4
16+0=16
max=16

16+0=16
15+0=15
max=16

15+0=15
1+0=1
max=15

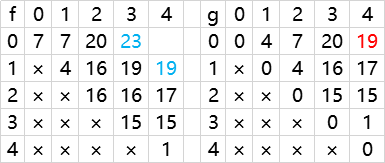
我们得出了 f 表新相对应可以求出镜像的 g 表

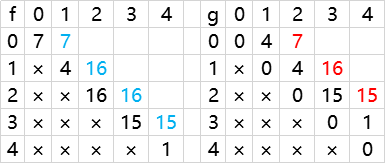
再反过来推导 f 表

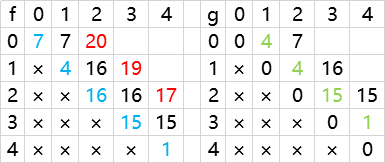
arr[0][2] = max( (7+4) , (16+4) ) =20
arr[1][3] = max( (4+15) , (15+4) ) =19
arr[2][4] = max( (16+1) , (1+15) ) =17

反推 g 表

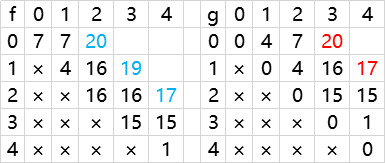
反推 f 表

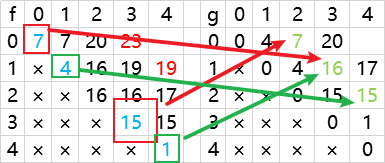
反推 g 表

反推 f 表

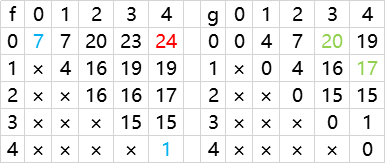
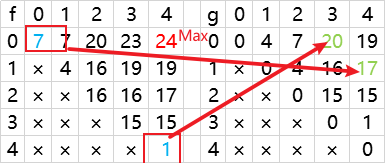
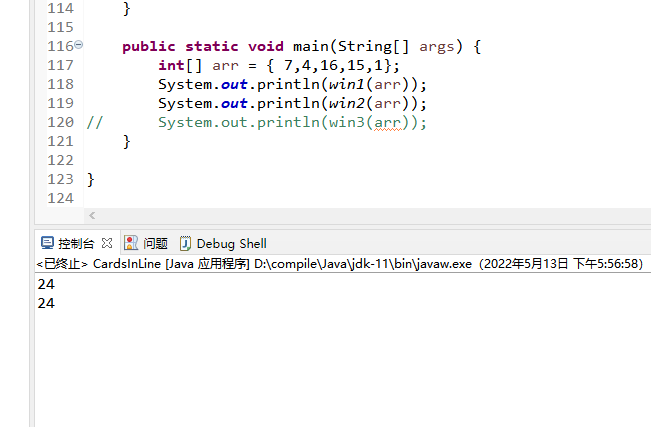
然后取 f[0][n-1] 和 g[0][n-1] 中最大值为答案

	public static int win3(int[] arr) {
		if (arr == null || arr.length == 0) {
			return 0;
		}
		int n = arr.length;
		int[][] f = new int[n][n];
		int[][] g = new int[n][n];
		for (int i = 0; i < n; i++) {
			// f表对角线
			f[i][i] = arr[i];
		}
		// startCol为列 0为对角线已经设置过了
		for (int startCol = 1; startCol < n; startCol++) {
			int row = 0; // 从第一行开始
			int col = startCol; // 从第几列开始 跳过对角线位置的
			while (col < n) {
				f[row][col] = Math.max(arr[row] + g[row + 1][col], arr[col] + g[row][col -1 ]);
				g[row][col] = Math.min(f[row + 1][col], f[row][col - 1]);
				row++;
				col++;

			}

		}
		return Math.max(f[0][n - 1], g[0][n - 1]);
	}

	public static void main(String[] args) {
		int[] arr = { 7, 4, 16, 15, 1 };
		System.out.println(win3(arr));
	}

01 背包

背包问题
给定两个长度都为N的数组weights和values，weights[i]和values[i]分别代表 i号物品的重量和价值
给定一个正数bag，表示一个载重bag的袋子，装的物品不能超过这个重量
返回能装下的最大价值

暴力递归

	public static int maxValue(int[] w, int[] v, int bag) {
		if (w == null || v == null || w.length != v.length || w.length == 0) {
			return 0;
		}
		return process(w, v, 0, bag);
	}

	/**
	 * 
	 * @param w     重量数组
	 * @param v     价值数组
	 * @param index 当前在哪个商品位置
	 * @param rest  当前背包剩余容量
	 * @return
	 */
	public static int process(int[] w, int[] v, int index, int rest) {
		// 背包容量为负数
		if (rest < 0) {
			// 返回-1用于标记为不规范
			return -1;
		}
		// 当前没有物品可以挑 数组越界
		if (index == w.length) {
			return 0;
		}
		// 没有要当前物品
		int p1 = process(w, v, index + 1, rest);
		int p2 = 0;
		// 要了当前物品
		int next = process(w, v, index + 1, rest - w[index]);
		// 返回符合规范 即不为-1
		if (next != -1) {
			p2 = v[index] + next;
		}
		return Math.max(p1, p2);
	}

	public static void main(String[] args) {
		int[] weights = { 3, 2, 4, 7, 3, 1, 7 };
		int[] values = { 5, 6, 3, 19, 12, 4, 2 };
		int bag = 15;
		System.out.println(maxValue(weights, values, bag));
	}

动态规划

通过 base case 发现 index 时 为 0

// 当前没有物品可以挑 数组越界
if (index == w.length) {
    return 0;
}

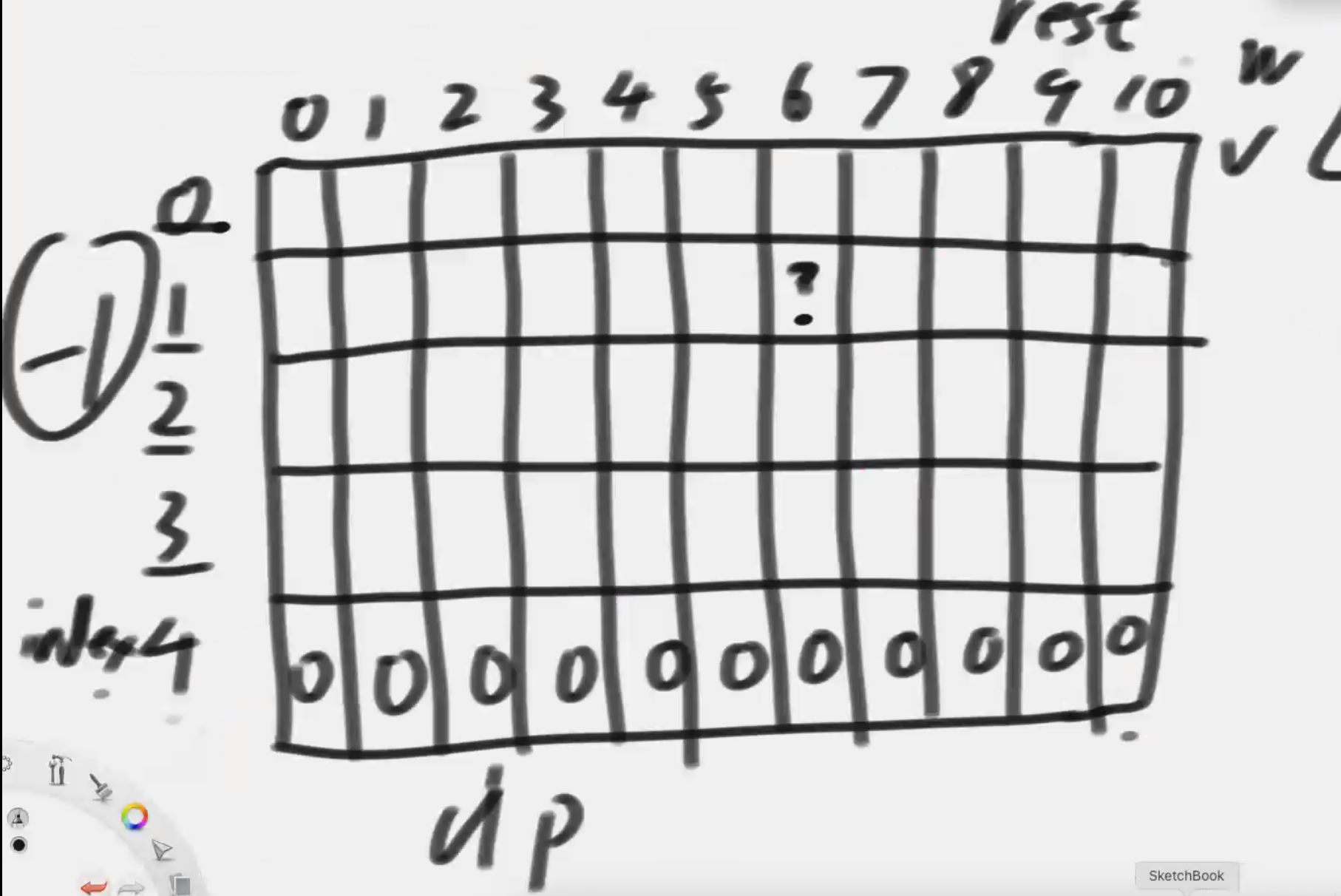
而每一行依赖是它的下一行出结果

1. 没有要当前物品 直接继承下一行的值
2. 要了当前物品 判断背包剩余容量是否规范 如规范则当前物品价格 + 下一行的值
3. 要了和没有要 做最大值

public static int dp(int[] w, int[] v, int bag) {
		if (w == null || v == null || w.length != v.length || w.length == 0) {
			return 0;
		}
		int n = w.length;
		int[][] dp = new int[n + 1][bag + 1];
		for (int index = n - 1; index >= 0; index--) {
			for (int rest = 0; rest <= bag; rest++) {
				int p1 = dp[index + 1][rest];
				int p2 = 0;
				int next = rest - w[index] < 0 ? -1 : dp[index + 1][rest - w[index]];
				if (next != -1) {
					p2 = v[index] + next;
				}
				dp[index][rest] = Math.max(p1, p2);
			}
		}
		return dp[0][bag];
	}

	public static void main(String[] args) {
		int[] weights = { 3, 2, 4, 7, 3, 1, 7 };
		int[] values = { 5, 6, 3, 19, 12, 4, 2 };
		int bag = 15;
		System.out.println(dp(weights, values, bag));
	}

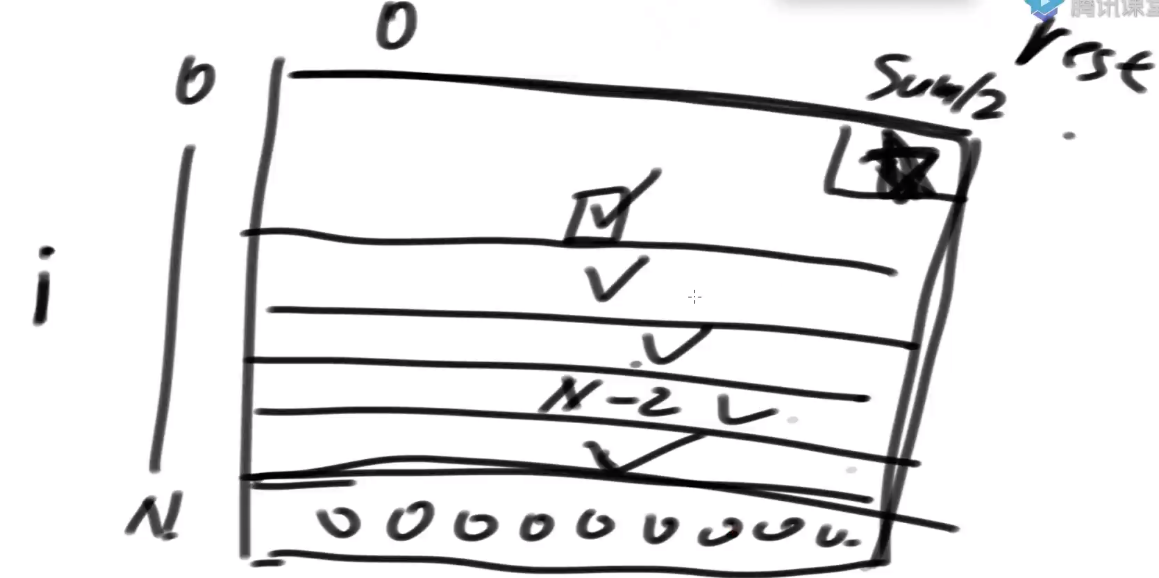
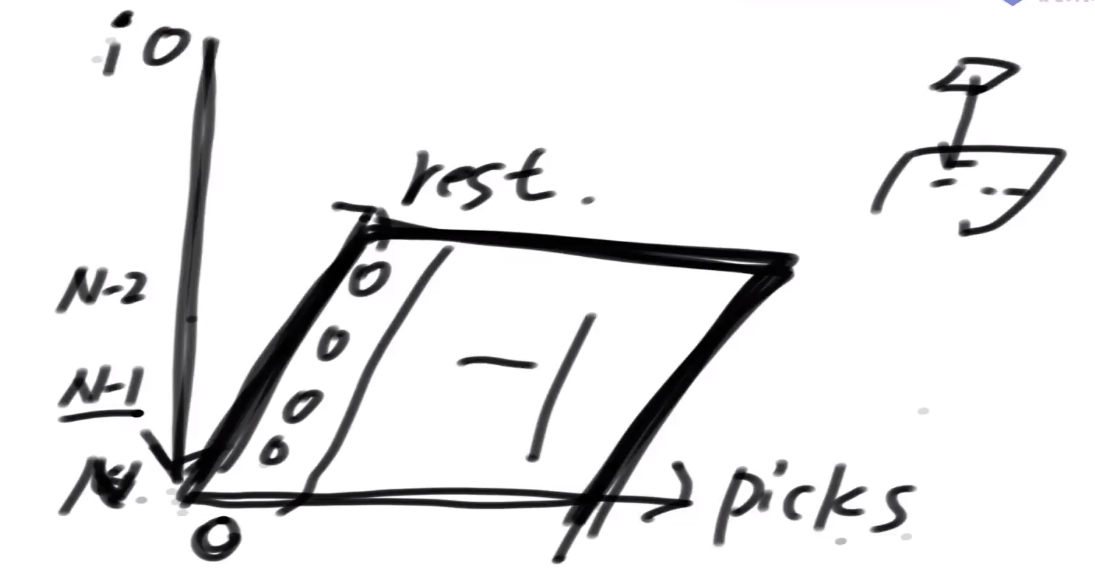
AcWing

这里是将第 0 行作为 base case

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int V = sc.nextInt();
        int[][] dp=new int[1010][1010];
        int[] v=new int[1010];
        int[] w=new int[1010];
        for (int i = 1; i <=n ; i++) {
            v[i]=sc.nextInt();
            w[i]=sc.nextInt();
        }
        for (int i = 1; i <=n ; i++) {
            for (int j = 0; j <= V; j++) {
                dp[i][j]=dp[i-1][j];  //复制为上一个物品的价格
                //当前j为背包容量从0开始到V实际背包容量结束
                if (j >= v[i]){  //关键代码  如当前背包容量大于或者等于当前物品v[i]的体积  则执行以下代码
                    dp[i][j]=Math.max(dp[i][j],dp[i-1][j-v[i]]+w[i]);  //比较价格  比较复制上一个价格  和
                }
            }
        }
        System.out.println(dp[n][V]);


    }
}

结合版

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int V = sc.nextInt();
        int[][] dp=new int[1010][1010];
        int[] v=new int[1010];
        int[] w=new int[1010];
        for (int i = 0; i <n ; i++) {
            v[i]=sc.nextInt();
            w[i]=sc.nextInt();
        }
        for (int i = n-1; i >=0 ; i--) {
            for (int j = 0; j <= V; j++) {
                dp[i][j]=dp[i+1][j];  //复制为上一个物品的价格
                //当前j为背包容量从0开始到V实际背包容量结束
                if (j >= v[i]){  //关键代码  如当前背包容量大于或者等于当前物品v[i]的体积  则执行以下代码
                    dp[i][j]=Math.max(dp[i][j],dp[i+1][j-v[i]]+w[i]);  //比较价格  比较复制上一个价格  和
                }
            }
        }
        System.out.println(dp[0][V]);


    }
}

字符转化

规定1和A对应、2和B对应、3和C对应...26和Z对应
那么一个数字字符串比如"111”就可以转化为:
"AAA"、"KA"和"AK"
给定一个只有数字字符组成的字符串str，返回有多少种转化结果

暴力递归

public static int number(String str) {
		if (str == null || str.length() == 0) {
			return 0;
		}
		return process(str.toCharArray(), 0);
	}

	/**
	 * 
	 * @param str 字符数组
	 * @param i   当前字符下标
	 * @return
	 */
	public static int process(char[] str, int i) {
		// 如果当前i已经到达字符串尾 说明前面的字符都是可以转换 直接返回+1次
		if (i == str.length) {
			return 1;
		}
		// 当前字符为单独的0 说明前面字符没有带上这0 或者 加上0之后超过27
		if (str[i] == '0') {
			// 说明本次转换不符合规范 直接返回0次
			return 0;
		}
		// 当前字符单个转换
		int ways = process(str, i + 1);
		// 如果i+1不越界 并且与后面数字结合不超过27 即可以与后一个字符两个进行转换
		if (i + 1 < str.length && (str[i] - '0') * 10 + (str[i + 1] - '0') < 27) {
			ways += process(str, i + 2);
		}
		return ways;
	}

动态规划

	// 从右到左的动态规划
	public static int dp1(String s) {
		if (s == null || s.length() == 0) {
			return 0;
		}
		char[] str = s.toCharArray();
		int n = str.length;
		int[] dp = new int[n + 1];
		dp[n] = 1;
		for (int i = n - 1; i >= 0; i--) {
			if (str[i] != '0') {
				int ways = dp[i + 1];
				if (i + 1 < str.length && (str[i] - '0') * 10 + (str[i + 1] - '0') < 27) {
					ways += dp[i + 2];
				}
				dp[i] = ways;
			}

		}
		return dp[0];
	}
	

	// 从左到右的动态规划
	public static int dp2(String s) {
		if (s == null || s.length() == 0) {
			return 0;
		}
		char[] str = s.toCharArray();
		if (str[0] == '0') {
			return 0;
		}
		int n = str.length;
		int[] dp = new int[n];
		dp[0] = 1;
		for (int i = 1; i < n; i++) {
			// 当前字符为0
			if (str[i] == '0') {
				/**
				 * str[i-1] == '0' 当前字符的前一个字符为0 00无法转换 str[i-2] > '2' 当前字符的前一个字符大于2 30超过27无法转换
				 * i-2 >= 0防止越界 dp[i-2]==0 如果当前字符合并前字符 并且 dp[i-2]==0 说明之前的字符都没有转换次数 直接返回0
				 */
				if (str[i - 1] == '0' || str[i - 1] > '2' || (i - 2 >= 0 && dp[i - 2] == 0)) {
					return 0;
				} else {

					dp[i] = i - 2 >= 0 ? dp[i - 2] : 1;
				}
			} else {
				//继承上个结果
				dp[i] = dp[i - 1];
				if (str[i - 1] != '0' && (str[i - 1] - '0') * 10 + str[i] - '0' < 27) {
					//
					dp[i] += i - 2 >= 0 ? dp[i - 2] : 1;
				}
			}
		}
		return dp[n - 1];

	}

691. 贴纸拼词 (opens new window)

给定一个字符串str，给定一个字符串类型的数组arr，出现的字符都是小写英文
arr每一个字符串，代表一张贴纸，你可以把单个字符剪开使用，目的是拼出str来
返回需要至少多少张贴纸可以完成这个任务
例子：str= "babac"，arr = {"ba","c","abcd"}
ba + ba + c  3  abcd + abcd 2  abcd+ba 2
所以返回2

暴力递归

暴力递归不要尝试提交 会超时

朴素法

public static int minStickers1(String[] stickers, String target) {
		int ans = process1(stickers, target);
		return ans == Integer.MAX_VALUE ? -1 : ans;
	}

	/**
	 * 
	 * @param stickers 剪纸数组
	 * @param target   目标字符
	 * @return
	 */
	public static int process1(String[] stickers, String target) {
		if (target.length() == 0) {
			return 0;
		}
		int min = Integer.MAX_VALUE;
		for (String first : stickers) {
			String rest = minus(target, first);
			// 经minus处理后 字符串变少了 说明当前first有使用到当前剪纸
			if (rest.length() != target.length()) {
				// 递归尝试是否能将rest全部剪完
				min = Math.min(min, process1(stickers, rest));
			}
		}
		// 如果min == Integer.MAX_VALUE说明没有命中if分支 即当前递归不能再剪了 不能+1否则int溢出所以+0
		// 如果min != Integer.MAX_VALUE说明命中了if分支 说明有剪到某些字符 加上first+1
		return min + (min == Integer.MAX_VALUE ? 0 : 1);
	}

	public static String minus(String s1, String s2) {
		char[] str1 = s1.toCharArray();// 目标字符数组
		char[] str2 = s2.toCharArray();// 剪纸字符数组
		int[] count = new int[26];
		for (char c : str1) {
			count[c - 'a']++;
		}
		for (char d : str2) {
			count[d - 'a']--;
		}
		StringBuffer sb = new StringBuffer();
		// 根据相减后的字符数组 做字符拼接 返回rest剩余字符串
		for (int i = 0; i < count.length; i++) {
			if (count[i] > 0) {
				for (int j = 0; j < count[i]; j++) {
					sb.append((char) (i + 'a'));
				}
			}
		}
		return sb.toString();
	}

优化剪纸写法

public static int minStickers2(String[] stickers, String target) {
		int n = stickers.length;
		// 创建一张二维表 用于存放每个剪纸的字符数组统计
		int[][] counts = new int[n][26];
		for (int i = 0; i < counts.length; i++) {
			char[] str = stickers[i].toCharArray();
			for (char c : str) {
				counts[i][c - 'a']++;
			}
		}
		int ans = process2(counts, target);
		return ans == Integer.MAX_VALUE ? -1 : ans;

	}

	/**
	 * 
	 * @param counts 剪纸的字符统计
	 * @param target 目标字符串
	 * @return
	 */
	public static int process2(int[][] counts, String target) {
		if (target.length() == 0) {
			return 0;
		}
		// 对目标字符串做词频
		char[] charArray = target.toCharArray();
		int[] tcounts = new int[26];
		for (char c : charArray) {
			tcounts[c - 'a']++;
		}

		int n = counts.length;
		int min = Integer.MAX_VALUE;
		for (int i = 0; i < n; i++) {
			// 尝试哪个剪纸
			int[] sticker = counts[i];
			// 剪枝策略 因为所有字符都做了字符统计
			// 如果target第一个字符 在剪纸中没出现过 说明当前尝试可以舍弃(总有可能会尝试到 但不是在此次递归中尝试)
			if (sticker[charArray[0] - 'a'] > 0) {
				StringBuffer sb = new StringBuffer();
				for (int j = 0; j < 26; j++) {
					// 当前字符在剪纸大于0
					if (tcounts[j] > 0) {
						// 作减法
						int nums = tcounts[j] - sticker[j];
						for (int k = 0; k < nums; k++) {
							// 剩下的字符 拼接为rest
							sb.append((char) (j + 'a'));
						}
					}
				}
				String rest = sb.toString();
				min = Math.min(min, process2(counts, rest));
			}
		}
		return min + (min == Integer.MAX_VALUE ? 0 : 1);
	}

记忆化搜索

public static int minStickers3(String[] stickers, String target) {
		int n = stickers.length;
		int[][] counts = new int[n][26];
		for (int i = 0; i < counts.length; i++) {
			char[] str = stickers[i].toCharArray();
			for (char c : str) {
				counts[i][c - 'a']++;
			}
		}

		HashMap<String, Integer> dp = new HashMap<>();
		// base case
		dp.put("", 0);
		// 带着缓存表递归
		int ans = process3(counts, target, dp);
		return ans == Integer.MAX_VALUE ? -1 : ans;

	}

	public static int process3(int[][] counts, String target, HashMap<String, Integer> dp) {
		// 缓存表中有直接返回
		if (dp.containsKey(target)) {
			return dp.get(target);
		}
		// 对目标字符串做词频
		char[] charArray = target.toCharArray();
		int[] tcounts = new int[26];
		for (char c : charArray) {
			tcounts[c - 'a']++;
		}

		int n = counts.length;
		int min = Integer.MAX_VALUE;
		for (int i = 0; i < n; i++) {
			// 尝试哪个剪纸
			int[] sticker = counts[i];
			// 剪枝策略 因为所有字符都做了字符统计
			// 如果target第一个字符 在剪纸中没出现过 说明当前尝试可以舍弃(总有可能会尝试到 但不是在此次递归中尝试)
			if (sticker[charArray[0] - 'a'] > 0) {
				StringBuffer sb = new StringBuffer();
				for (int j = 0; j < 26; j++) {
					// 当前字符在剪纸大于0
					if (tcounts[j] > 0) {
						// 作减法
						int nums = tcounts[j] - sticker[j];
						for (int k = 0; k < nums; k++) {
							// 剩下的字符 拼接为rest
							sb.append((char) (j + 'a'));
						}
					}
				}
				String rest = sb.toString();
				min = Math.min(min, process3(counts, rest));
			}
		}
		int ans = min + (min == Integer.MAX_VALUE ? 0 : 1);
		// 算完放入缓存
		dp.put(target, ans);
		return ans;

	}

1143. 最长公共子序列 (opens new window)

暴力递归

public int longestCommonSubsequence1(String s1, String s2) {
		if (s1 == null || s2 == null || s1.length() == 0 || s2.length() == 0) {
			return 0;
		}
		char[] str1 = s1.toCharArray();
		char[] str2 = s2.toCharArray();
		return process1(str1, str2, str1.length - 1, str2.length - 1);
	}

	/**
	 * 可能性分类: 1. 一定不以str1[i]字符结尾 也一定不以str2[j]字符结尾 
	 * 2. 可能以str1[i]字符结尾 但一定不以str2[j]字符结尾
	 * 3. 一定不以str1[i]字符结尾 但可能以str2[j]子符结尾 
	 * 4. 必须以str1[i]字符结尾 也必须以str2[j]字符结尾
	 * 
	 * @param str1 字符串1
	 * @param str2 字符串2
	 * @param i    str1[0...i]和str2[0...j]，这个范围上最长公共子序列长度是多少?
	 * @param j
	 * @return 最长公共子序列长度
	 */
	public int process1(char[] str1, char[] str2, int i, int j) {
		if (i == 0 && j == 0) {
			// str1和str2只剩下一个字符 下标为0的字符 两字符相同返回+1长度 否则返回0
			return str1[i] == str2[j] ? 1 : 0;
		} else if (i == 0) {
			// str1只剩一个字符 但str2不只一个字符
			if (str1[i] == str2[j]) {
				return 1;
			} else {
				// 不相同 str2继续减少
				return process1(str1, str2, i, j - 1);
			}
		} else if (j == 0) {
			// str2只剩一个字符 但str1不只一个字符
			if (str1[i] == str2[j]) {
				return 1;
			} else {
				// str2不变 str1继续减少
				return process1(str1, str2, i - 1, j);
			}
		} else {
			// str1和str2都不单只一个字符
			// str1减少情况
			int p1 = process1(str1, str2, i - 1, j);
			// str2减少情况
			int p2 = process1(str1, str2, i, j - 1);
			// 首先判断当前str1[i]和str2[j]是否相同 如果相同则代表当前字符也是长度1的子序列并同时减少str1和str2
			int p3 = str1[i] == str2[j] ? (1 + process1(str1, str2, i - 1, j - 1)) : 0;
			return Math.max(p1, Math.max(p2, p3));
		}

	}

动态规划

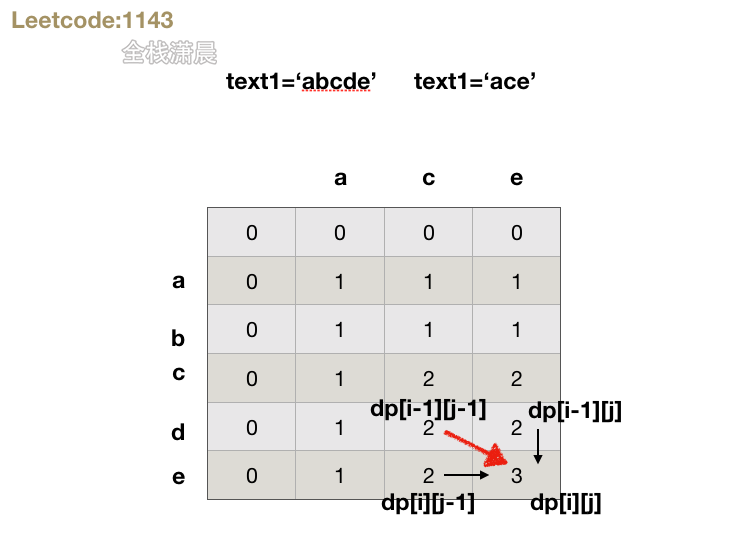
public int longestCommonSubsequence(String s1, String s2) {
		if (s1 == null || s2 == null || s1.length() == 0 || s2.length() == 0) {
			return 0;
		}
		char[] str1 = s1.toCharArray();
		char[] str2 = s2.toCharArray();
		int n = str1.length;
		int m = str2.length;
		int[][] dp = new int[n][m];
		// base case1
		dp[0][0] = str1[0] == str2[0] ? 1 : 0;
		// base case2
		for (int j = 1; j < m; j++) {
			dp[0][j] = str1[0] == str2[j] ? 1 : dp[0][j - 1];
		}
		// base case3
		for (int i = 1; i < n; i++) {
			dp[i][0] = str1[i] == str2[0] ? 1 : dp[i - 1][0];
		}
		// other
		for (int i = 1; i < n; i++) {
			for (int j = 1; j < m; j++) {
				int p1 = dp[i - 1][j];
				int p2 = dp[i][j - 1];
				int p3 = str1[i] == str2[j] ? (1 + dp[i - 1][j - 1]) : 0;
				dp[i][j] = Math.max(p1, Math.max(p2, p3));
			}
		}
		return dp[n - 1][m - 1];
	}

516. 最长回文子序列 (opens new window)

解法 1. 可以在最长公共子序列解法中 将原始字符串反转求两字符串最长公共子序列即是答案

暴力递归

	public static int lpsl1(String s) {
		if (s == null || s.length() == 0) {
			return 0;
		}

		char[] str = s.toCharArray();
		return process1(str, 0, str.length - 1);
	}

	public static int process1(char[] str, int l, int r) {
		// 只剩一个字符 肯定是回文
		if (l == r) {
			return 1;
		}
		// 只剩两个字符 分情况
		if (l == r - 1) {
			return str[l] == str[r] ? 2 : 1;
		}
		// 字符串头和尾同时收缩 即不以l开头 也不以r结尾
		int p1 = process1(str, l + 1, r - 1);
		// 字符串头收缩 不以l开头 以r结尾
		int p2 = process1(str, l + 1, r);
		// 字符串尾收缩 以l开头 不以r结尾
		int p3 = process1(str, l, r - 1);
		// 如果当前字符串的头和尾 相等则需要将此时2个字符统计上去 否则不作处理 即以l开头 也以r结尾
		int p4 = str[l] == str[r] ? 2 + process1(str, l + 1, r - 1) : 0;

		return Math.max(Math.max(p1, p2), Math.max(p3, p4));
	}

动态规划

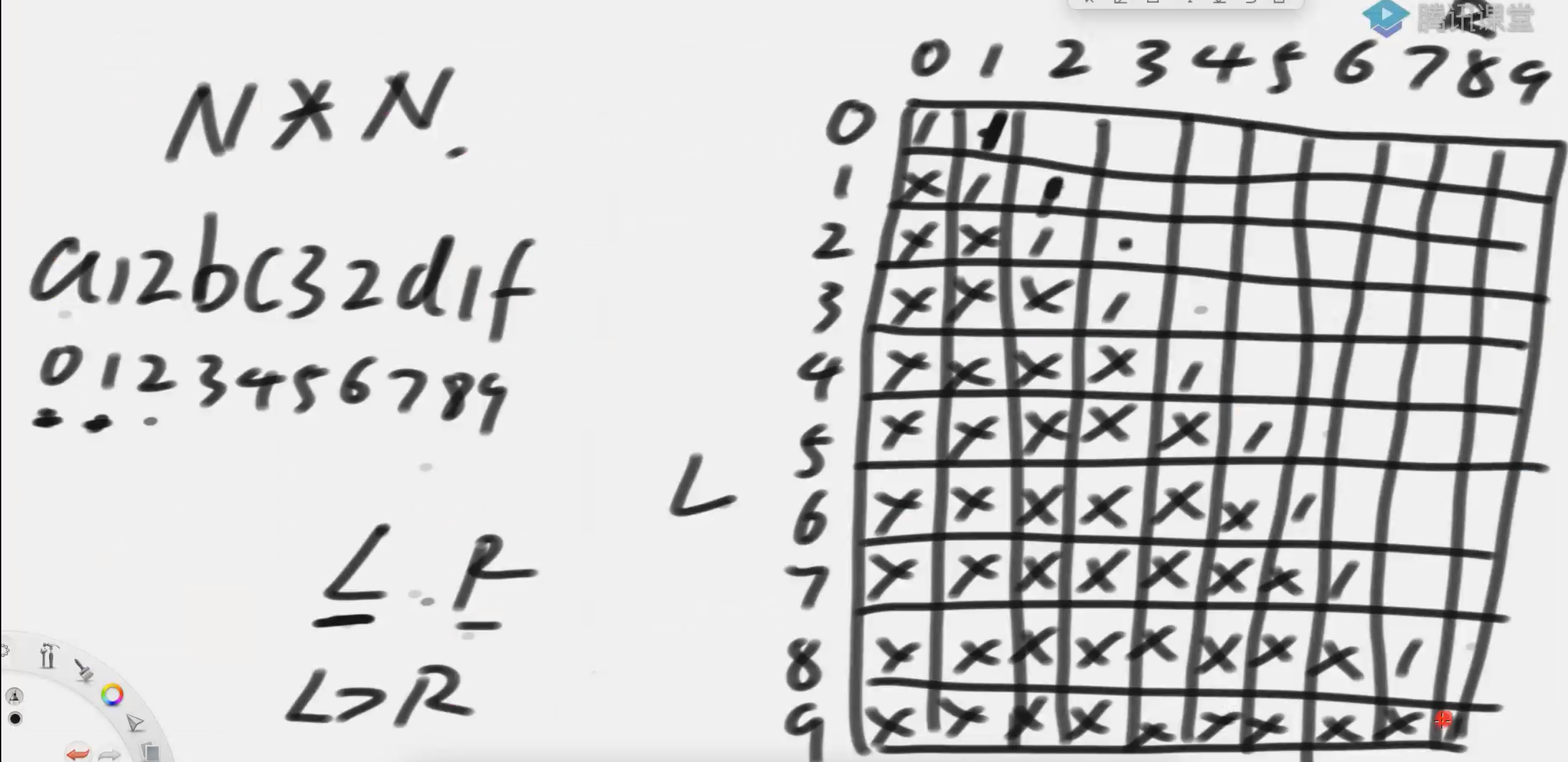
		//先填上右下角的 方便对角线和对角线+1填值
		dp[n-1][n-1] = 1;
		for (int i = 0; i < n-1; i++) {
			//base case1
			dp[i][i] = 1;
			//base case2
			dp[i][i+1] = str[i] ==str[i+1] ? 2:1;
		}

填完对角线和对角线 + 1 位置后 分析依赖发现求一个未知值它依赖是它的左边、左下角和下边的值

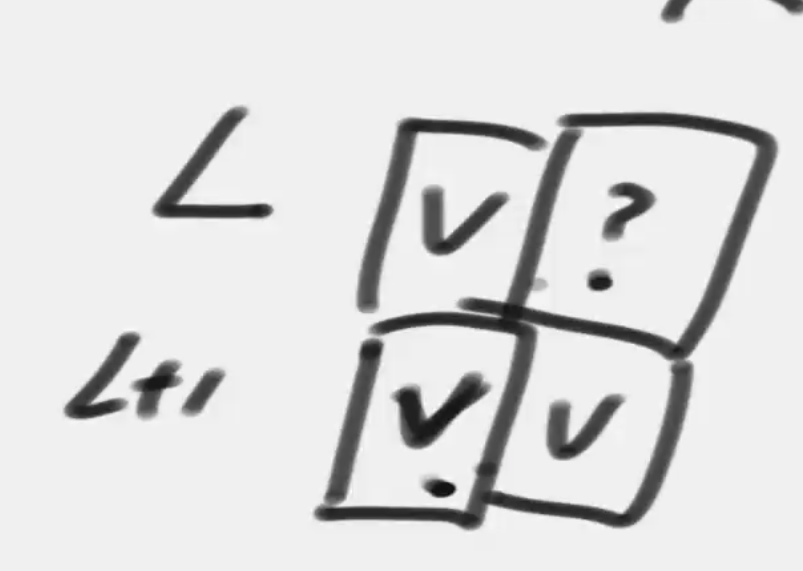
	public static int lpsl2(String s) {
		if (s == null || s.length() == 0) {
			return 0;
		}
		char[] str = s.toCharArray();
		int n = str.length;
		int[][] dp = new int[n][n];
		// 先填上右下角的 方便对角线和对角线+1填值
		dp[n - 1][n - 1] = 1;
		for (int i = 0; i < n - 1; i++) {
			// base case1
			dp[i][i] = 1;
			// base case2
			dp[i][i + 1] = str[i] == str[i + 1] ? 2 : 1;
		}

		for (int l = n - 3; l >= 0; l--) {
			for (int r = l + 2; r < n; r++) {
				// 字符串头和尾同时收缩 即不以l开头 也不以r结尾
				int p1 = dp[l + 1][r - 1];
				// 字符串头收缩 不以l开头 以r结尾
				int p2 = dp[l + 1][r];
				// 字符串尾收缩 以l开头 不以r结尾
				int p3 = dp[l][r - 1];
				// 如果当前字符串的头和尾 相等则需要将此时2个字符统计上去 否则不作处理 即以l开头 也以r结尾
				int p4 = str[l] == str[r] ? 2 + dp[l + 1][r - 1] : 0;
				dp[l][r] = Math.max(Math.max(p1, p2), Math.max(p3, p4));
			}
		}

		return dp[0][n - 1];
	}

优化

通过上面 dp 解法我们发现 一个未知位置的值它依赖的是它的 左下、左、下、2 + 左中最大值 而它的左和下，也依赖过左下又是求的是最大值，所以左和下不可能比左下小，我们可以把左下的依赖去掉，只有当 str [l] 和 str [r] 相等时才求出 2 + 左下

	public static int lpsl3(String s) {
		if (s == null || s.length() == 0) {
			return 0;
		}
		char[] str = s.toCharArray();
		int n = str.length;
		int[][] dp = new int[n][n];
		// 先填上右下角的 方便对角线和对角线+1填值
		dp[n - 1][n - 1] = 1;
		for (int i = 0; i < n - 1; i++) {
			// base case1
			dp[i][i] = 1;
			// base case2
			dp[i][i + 1] = str[i] == str[i + 1] ? 2 : 1;
		}

		for (int l = n - 3; l >= 0; l--) {
			for (int r = l + 2; r < n; r++) {
				// 字符串头收缩 不以l开头 以r结尾
				int p2 = dp[l + 1][r];
				// 字符串尾收缩 以l开头 不以r结尾
				int p3 = dp[l][r - 1];
				dp[l][r] = Math.max(p2, p3);
				if (str[l] == str[r]) {
					dp[l][r] = Math.max(dp[l][r], 2 + dp[l + 1][r - 1]);
				}
			}
		}

		return dp[0][n - 1];
	}

马的遍历

请同学们自行搜索或者想象一个象棋的棋盘，
然后把整个棋盘放入第一象限，棋盘的最左下角是(0,0)位置
那么整个棋盘就是横坐标上9条线、纵坐标上10条线的区域
给你三个 参数 x，y，k
返回“马”从(0,0)位置出发，必须走k步
最后落在(x,y)上的方法数有多少种? 

马走日 8 种跳的方法

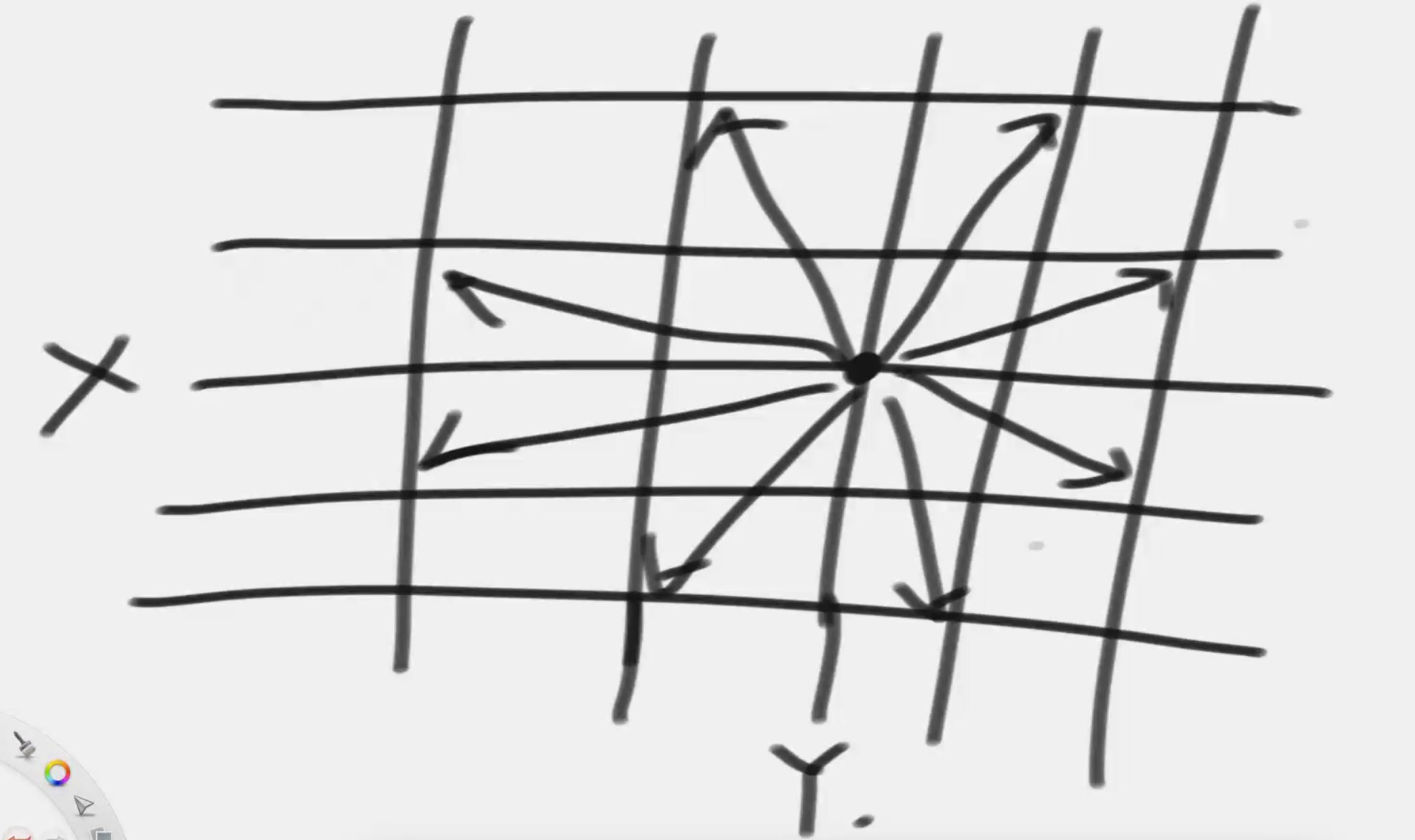
暴力递归

/**
 * 
 * @param a 目标x坐标
 * @param b 目标y坐标
 * @param k 要走多少不
 * @return
 */
public static int jump(int a, int b, int k) {
	return process(0, 0, k, a, b);
}

public static int process(int x, int y, int rest, int a, int b) {
	// 越界base case
	if (x < 0 || x > 9 || y < 0 || y > 8) {
		return 0;
	}
	if (rest == 0) {
		// 当前步数为0 并且当前位置在目标位置 次数+1
		return (x == a && y == b) ? 1 : 0;
	}

	int ways = process(x + 2, y + 1, rest - 1, a, b);
	ways += process(x + 1, y + 2, rest - 1, a, b);
	ways += process(x - 1, y + 2, rest - 1, a, b);
	ways += process(x - 2, y + 1, rest - 1, a, b);
	ways += process(x - 2, y - 1, rest - 1, a, b);
	ways += process(x - 1, y - 2, rest - 1, a, b);
	ways += process(x + 1, y - 2, rest - 1, a, b);
	ways += process(x + 2, y - 1, rest - 1, a, b);
	return ways;
}

动态规划

	public static int dp(int a, int b, int k) {
		int[][][] dp = new int[10][9][k + 1];
		// 当前剩余步数为0 并且在目标位置 为0 base case2
		dp[a][b][0] = 1;
		for (int rest = 1; rest <= k; rest++) {
			for (int x = 0; x < 10; x++) {
				for (int y = 0; y < 9; y++) {
					int ways = pick(dp, x + 2, y + 1, rest - 1);
					ways += pick(dp, x + 1, y + 2, rest - 1);
					ways += pick(dp, x - 1, y + 2, rest - 1);
					ways += pick(dp, x - 2, y + 1, rest - 1);
					ways += pick(dp, x - 2, y - 1, rest - 1);
					ways += pick(dp, x - 1, y - 2, rest - 1);
					ways += pick(dp, x + 1, y - 2, rest - 1);
					ways += pick(dp, x + 2, y - 1, rest - 1);
					dp[x][y][rest] = ways;

				}
			}
		}
		return dp[0][0][k];
	}

	// 防止越界方法
	public static int pick(int[][][] dp, int x, int y, int rest) {
		if (x < 0 || x > 9 || y < 0 || y > 8) {
			return 0;
		}
		return dp[x][y][rest];
	}

泡咖啡

给定一个数组arr，arr[i]代表第i号咖啡机泡一杯咖啡的时间
给定一个正数N，表示N个人等着咖啡机泡咖啡，每台咖啡机只能轮流泡咖啡
只有一台咖啡机，一次只能洗一个杯子，时间耗费a，洗完才能洗下一杯
每个咖啡杯也可以自己挥发干净，时间耗费b，咖啡杯可以并行挥发
假设所有人拿到咖啡之后立刻喝干净，
返回从开始等到所有咖啡机变干净的最短时间
三个参数：int[] arr、int N，int a、int b

暴力递归 + 贪心

	public static class Machine {
		public int timePoint; // 咖啡机什么时候空闲(即当前时间可以泡一杯咖啡)
		public int workTime; // 泡一杯咖啡要耗时多久

		public Machine(int timePoint, int workTime) {
			this.timePoint = timePoint;
			this.workTime = workTime;
		}

	}

	/**
	 * 计算每个人泡完咖啡的最短时间
	 * 
	 * @param arr arr[i]代表第i号咖啡机泡一杯咖啡的时间
	 * @param n   有多少个人泡咖啡
	 * @param a   洗杯子耗费的时间
	 * @param b   挥发耗费时间
	 * @return
	 */
	public static int minTime1(int[] arr, int n, int a, int b) {
		PriorityQueue<Machine> heap = new PriorityQueue<>((o1, o2) -> {
			// 泡完咖啡时长小在前面
			return (o1.timePoint + o1.workTime) - (o2.timePoint + o2.workTime);
		});
		for (int i = 0; i < arr.length; i++) {
			// 初始化所有咖啡机 在0号时间点空闲 需要arr[i]的时间才泡完
			heap.add(new Machine(0, arr[i]));
		}
		// 存储每个人最短时间泡完咖啡的时间
		int[] drinks = new int[n];
		for (int i = 0; i < n; i++) {
			// 从小根堆中弹出 当前时间点空闲咖啡机花费最少时间泡的咖啡
			Machine cur = heap.poll();
			// 空闲时间加上 泡完的工作时间
			cur.timePoint += cur.workTime;
			// 最短时间为 泡完的工作时间
			drinks[i] = cur.timePoint;
			heap.add(cur);
		}
		// 从第0个开始洗咖啡杯 0号时间点洗咖啡机空闲
		return bestTime(drinks, a, b, 0, 0);

	}

	/**
	 * 
	 * @param drinks 每个人泡完咖啡的最短时间
	 * @param wash   洗杯子机器要耗时多久洗完一个杯子
	 * @param air    咖啡挥发的时长
	 * @param index  从第几个人开始洗/挥发
	 * @param free   洗杯子的机器在什么时间点空闲(即什么时间可用)
	 * @return
	 */
	public static int bestTime(int[] drinks, int wash, int air, int index, int free) {
		// 当前越界返回0
		if (index == drinks.length) {
			return 0;
		}
		// 当前杯子决定洗
		// 咖啡泡完时间和洗杯子机器空闲时间 取最大值
		int selfClean1 = Math.max(drinks[index], free) + wash;
		// 剩下的杯子 递归 因为当前决策是洗杯子 所以洗杯子的空闲时间要进行传递
		int restClean1 = bestTime(drinks, wash, air, index + 1, selfClean1);
		// 取第一名和剩下人 洗完杯子的最大值
		int p1 = Math.max(selfClean1, restClean1);

		// 当前杯子决定挥发
		int selfClean2 = drinks[index] + air;
		// 因为当前决策是挥发没有占用洗杯子机器 所以洗杯子机器空闲时间没有变化
		int restClean2 = bestTime(drinks, wash, air, index + 1, free);
		// 还是第一和剩下取最大值
		int p2 = Math.max(selfClean2, restClean2);

		// 返回这两个决策中最小的一个
		return Math.min(p1, p2);
	}

动态规划

	public static class Machine {
		public int timePoint; // 咖啡机什么时候空闲(即当前时间可以泡一杯咖啡)
		public int workTime; // 泡一杯咖啡要耗时多久

		public Machine(int timePoint, int workTime) {
			this.timePoint = timePoint;
			this.workTime = workTime;
		}

	}

	/**
	 * 计算每个人泡完咖啡的最短时间
	 * 
	 * @param arr arr[i]代表第i号咖啡机泡一杯咖啡的时间
	 * @param n   有多少个人泡咖啡
	 * @param a   洗杯子耗费的时间
	 * @param b   挥发耗费时间
	 * @return
	 */
	public static int minTime2(int[] arr, int n, int a, int b) {
		PriorityQueue<Machine> heap = new PriorityQueue<>((o1, o2) -> {
			// 泡完咖啡时长小在前面
			return (o1.timePoint + o1.workTime) - (o2.timePoint + o2.workTime);
		});
		for (int i = 0; i < arr.length; i++) {
			// 初始化所有咖啡机 在0号时间点空闲 需要arr[i]的时间才泡完
			heap.add(new Machine(0, arr[i]));
		}
		// 存储每个人最短时间泡完咖啡的时间
		int[] drinks = new int[n];
		for (int i = 0; i < n; i++) {
			// 从小根堆中弹出 当前时间点空闲咖啡机花费最少时间泡的咖啡
			Machine cur = heap.poll();
			// 空闲时间加上 泡完的工作时间
			cur.timePoint += cur.workTime;
			// 最短时间为 泡完的工作时间
			drinks[i] = cur.timePoint;
			heap.add(cur);
		}
		return bestTimeDp(drinks, a, b);

	}

	/**
	 * 动态规划
	 * 
	 * @param drinks 每个人泡完咖啡的最短时间
	 * @param wash   洗杯子耗时
	 * @param air    挥发耗时
	 * @return
	 */
	public static int bestTimeDp(int[] drinks, int wash, int air) {
		int n = drinks.length;
		// 业务范围模型 假设最差的情况作范围
		int maxFree = 0;
		for (int i = 0; i < n; i++) {
			// 即假设每个杯子都要进行洗杯子 在洗杯子机器空闲时间和当前人泡完咖啡的时间 作最大值选择
			maxFree = Math.max(maxFree, drinks[i]) + wash;
		}
		int[][] dp = new int[n + 1][maxFree + 1];
		for (int index = n - 1; index >= 0; index--) {
			for (int free = 0; free <= maxFree; free++) {
				// 当前杯子决定洗 从过了最差情况的范围 直接跳过
				int selfClean1 = Math.max(drinks[index], free) + wash;
				if (selfClean1 > maxFree) {
					continue;
				}
				// 当前杯子决定洗
				// 咖啡泡完时间和洗杯子机器空闲时间 取最大值
				// int selfClean1 = Math.max(drinks[index], free) + wash;
				// 剩下的杯子 递归 因为当前决策是洗杯子 所以洗杯子的空闲时间要进行传递
				int restClean1 = dp[index + 1][selfClean1];
				// 取第一名和剩下人 洗完杯子的最大值
				int p1 = Math.max(selfClean1, restClean1);

				// 当前杯子决定挥发
				int selfClean2 = drinks[index] + air;
				// 因为当前决策是挥发没有占用洗杯子机器 所以洗杯子机器空闲时间没有变化
				int restClean2 = dp[index + 1][free];
				// 还是第一和剩下取最大值
				int p2 = Math.max(selfClean2, restClean2);

				// 返回这两个决策中最小的一个
				dp[index][free] = Math.min(p1, p2);

			}
		}
		return dp[0][0];
	}

空间压缩

给定一个二维数组matrix，一个人必须从左上角出发，最后到达右下角
沿途只可以向下或者向右走，沿途的数字都累加就是距离累加和
返回最小距离累加和

无压缩

	// 无空间压缩dp
	public static int minPathSum1(int[][] arr) {
		if (arr == null || arr.length == 0) {
			return 0;
		}
		int row = arr.length;
		int col = arr[0].length;
		int[][] dp = new int[row][col];
		dp[0][0] = arr[0][0];
		// 第一行从开头出发到当前数的最小累计和 只依赖于左
		for (int i = 1; i < row; i++) {
			dp[i][0] = dp[i - 1][0] + arr[i][0];
		}
		// 第一列开头出发到当前数的最小累计和 只依赖于上
		for (int i = 1; i < col; i++) {
			dp[0][i] = dp[0][i - 1] + arr[0][i];
		}
		// 其他位置 依赖左和上
		for (int i = 1; i < row; i++) {
			for (int j = 1; j < col; j++) {
				dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + arr[i][j];
			}
		}
		return dp[row - 1][col - 1];

	}

将二维数组压缩至一维

	/*
	 * 通过上面的dp我们发现每个数只依赖当前行左边数和上一行的上边数 而第一行和第一列只依赖一个方向 我们可以进行空间压缩 只使用一个一维数组来存储
	 * 不断更新这个一维数组直到终点
	 */
	public static int minPathSum2(int[][] arr) {
		if (arr == null || arr.length == 0) {
			return 0;
		}
		int row = arr.length;
		int col = arr[0].length;
		int[] dp = new int[col];
		dp[0] = arr[0][0];
		// 第一行 只依赖左方
		for (int i = 1; i < col; i++) {
			dp[i] = dp[i - 1] + arr[0][i];
		}
		// 其他行
		for (int i = 1; i < row; i++) {
			// 当前行第一个(即当前行第一列的数) 只依赖于上方 直接相加 因为没有其他更好的方案
			dp[0] += arr[i][0];
			for (int j = 1; j < col; j++) {
				//左边和当前位置(即上一行的上边的数)作最小选择
				dp[j] = Math.min(dp[j - 1], dp[j]) + arr[i][j];
			}
		}
		
		return dp[col-1];
	}

空间压缩技巧

通常我们进行分析动态规划每个数之间的依赖才能进行空间压缩 有以下几点技巧

1. 选择较小的一方进行压缩 如行比较小 就使用行数作 dp 的长度 竖向扩展 如列比较小 就使用列数作 dp 的长度 横向扩展

2. 左和上依赖

   从左到右逐个依赖压缩

3. 左上和上依赖

   从右到左逐个依赖压缩

4. 左、左上和上依赖

   使用 temp 变量缓存记录当前即将被更新的数值 (即作为下一个位置的左上依赖)

   然后从左到右逐个依赖

状态转移

DP 问题的核心即确定动态转移方程。

1. 寻找递归变量，确定子问题。DP 表一般为二维，故需要两个变量。
2. 寻找总问题与子问题迭代关系，确定中间值、迭代值

货币问题 1 (01 背包问题)

arr是货币数组，其中的值都是正数。再给定一个正数aim。
每个值都认为是一张货币，
即便是值相同的货币也认为每一张都是不同的，
返回组成aim的方法数
例如：arr = {1,1,1}，aim = 2
第0个和第1个能组成2，第1个和第2个能组成2，第0个和第2个能组成2
一共就3种方法，所以返回3

暴力递归

	/**
	 * 
	 * @param arr 货币数组
	 * @param aim 目标金额
	 * @return
	 */
	public static int coinWays(int[] arr, int aim) {
		return process(arr, 0, aim);
	}

	/**
	 * 
	 * @param arr   货币数组
	 * @param index 当前货币数值
	 * @param rest  剩余金额
	 * @return
	 */
	public static int process(int[] arr, int index, int rest) {
		// 当前剩余金额小于0 凑多了直接返回0次结果结束
		if (rest < 0) {
			return 0;
		}
		// 当前没有货币了
		if (index == arr.length) {
			// 没有货币并且剩余金额为0 则说明刚好凑够目标金额 返回1次
			return rest == 0 ? 1 : 0;
		}
		// 没有选取当前货币 + 选取了当前货币
		return process(arr, index + 1, rest) + process(arr, index + 1, rest - arr[index]);
	}

动态规划

	public static int dp(int[] arr, int aim) {
		if (aim == 0) {
			return 1;
		}
		int n = arr.length;
		int[][] dp = new int[n + 1][aim + 1];
		// 货币用完 并且剩余0元 记录为1次
		dp[n][0] = 1;
		for (int index = n - 1; index >= 0; index--) {
			for (int rest = 0; rest <= aim; rest++) {
				//没有选取当前货币情况
				dp[index][rest] = dp[index + 1][rest];
				//保证选取当前货币 剩余金额不小于0
				if (rest - arr[index] >= 0) {
					//选取当前货币的情况
					dp[index][rest] += dp[index + 1][rest - arr[index]];
				}
			}
		}
		return dp[0][aim];
	}

货币问题 2 (完全背包问题)

arr是面值数组，其中的值都是正数且没有重复。再给定一个正数aim。
每个值都认为是一种面值，且认为张数是无限的。
返回组成aim的方法数
例如：arr = {1,2}，aim = 4
方法如下：1+1+1+1、1+1+2、2+2
一共就3种方法，所以返回3

暴力递归

	public static int coinsWay(int[] arr, int aim) {
		if (arr == null || arr.length == 0 || aim < 0) {
			return 0;
		}
		return process(arr, 0, aim);
	}

	/**
	 * 
	 * @param arr   面值数组
	 * @param index 当前位置
	 * @param rest  凑到目标的剩余金额
	 * @return
	 */
	public static int process(int[] arr, int index, int rest) {
		// 没有面值了
		if (index == arr.length) {
			// 剩余金额为0则返回1次 否则返回0次
			return rest == 0 ? 1 : 0;
		}
		int ways = 0;
		// 选取当前位置面值 从0张开始凑直到大于rest
		for (int zhang = 0; zhang * arr[index] <= rest; zhang++) {
			ways += process(arr, index + 1, rest - (zhang * arr[index]));
		}
		return ways;
	}

动态规划

public static int dp1(int[] arr, int aim) {
		if (arr == null || arr.length == 0 || aim < 0) {
			return 0;
		}
		int n = arr.length;
		int[][] dp = new int[n + 1][aim + 1];
		dp[n][0] = 1;
		for (int index = n - 1; index >= 0; index--) {
			for (int rest = 0; rest <= aim; rest++) {
				int ways = 0;
				// 选取当前位置面值 从0张开始凑直到大于rest
				for (int zhang = 0; zhang * arr[index] <= rest; zhang++) {
					ways += dp[index + 1][rest - (zhang * arr[index])];
				}
				dp[index][rest] = ways;
			}
		}
		
		return dp[0][aim];
	}

状态转移

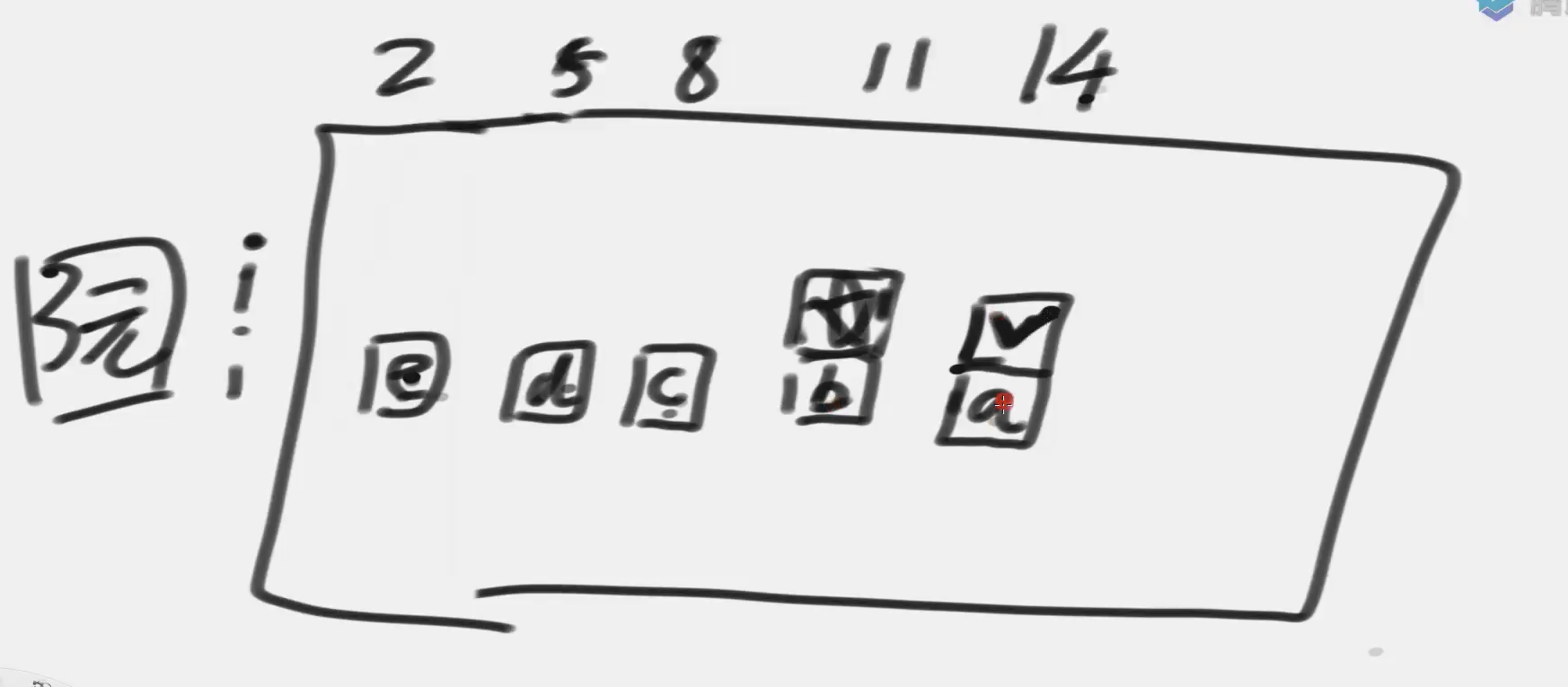
通过表的依赖关系发现 dp[index][rest]=dp[index][rest-arr[index]] + dp[index+1][rest]

即星号的位置的值为 e+d+c+b

而我们要求的位置的值为 e+d+c+b+ a

我们发现前面我们求过 e+d+c+b 这个值 可以优化掉这个第三层的 for 循环

for (int zhang = 0; zhang * arr[index] <= rest; zhang++) {
    ways += dp[index + 1][rest - (zhang * arr[index])];
}

变成

dp[index][rest] = dp[index+1][rest];
if(rest-arr[index] >= 0) {
    dp[index][rest] +=dp[index][rest-arr[index]];
}

这个就是所谓的状态转移 我们可以通过严格的表依赖来进行分析优化 转移已经做过的步骤

完整代码

public static int dp2(int[] arr,int aim) {
		if (arr == null || arr.length == 0 || aim < 0) {
			return 0;
		}
		int n = arr.length;
		int[][] dp = new int[n + 1][aim + 1];
		dp[n][0] = 1;
		for (int index = n - 1; index >= 0; index--) {
			for (int rest = 0; rest <= aim; rest++) {
				dp[index][rest] = dp[index+1][rest];
				if(rest-arr[index] >= 0) {
					dp[index][rest] +=dp[index][rest-arr[index]];
				}
				
			}
		}
		
		return dp[0][aim];
	}

货币问题 3 (多重背包问题)

arr是货币数组，其中的值都是正数。再给定一个正数aim。
每个值都认为是一张货币，
认为值相同的货币没有任何不同，
返回组成aim的方法数
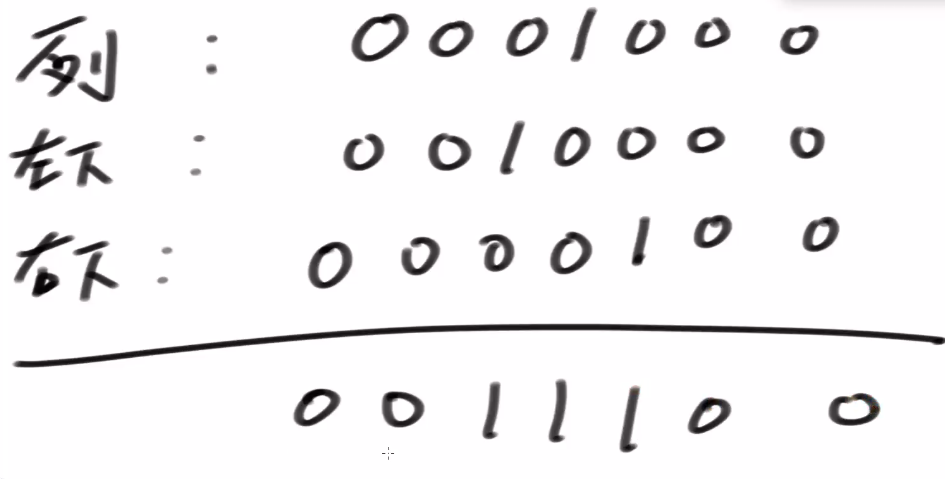
例如：arr = {1,2,1,1,2,1,2}，aim = 4
方法：1+1+1+1、1+1+2、2+2
一共就3种方法，所以返回3

暴力递归

	public static class info {
		public int[] coins; // 去重后的货币类型
		public int[] zhangs; // 每个货币对应的数量

		public info(int[] coins, int[] zhangs) {
			this.coins = coins;
			this.zhangs = zhangs;
		}

	}

	// 给定一个货币数组 返回去重后的货币类型 和 每个货币对应的数量两数组
	public static info getInfo(int[] arr) {
		HashMap<Integer, Integer> map = new HashMap<>();
		for (int value : arr) {
			if (!map.containsKey(value)) {
				map.put(value, 1);
			} else {
				map.put(value, map.get(value) + 1);
			}
		}
		int n = map.size();
		int[] coins = new int[n];
		int[] zhangs = new int[n];
		int index = 0;
		for (Entry<Integer, Integer> entry : map.entrySet()) {
			coins[index] = entry.getKey();
			zhangs[index++] = entry.getValue();
		}
		return new info(coins, zhangs);
	}

	public static int coinsWay(int[] arr, int aim) {
		if (arr == null || arr.length == 0 || aim < 0) {
			return 0;
		}
		info in = getInfo(arr);
		return process(in.coins, in.zhangs, 0, aim);
	}

	/**
	 * 
	 * @param coins  货币类型
	 * @param zhangs 货币对应的张数
	 * @param index  当前位置
	 * @param rest   剩余金额
	 * @return
	 */
	public static int process(int[] coins, int[] zhangs, int index, int rest) {
		if (index == coins.length) {
			return rest == 0 ? 1 : 0;
		}
		int ways = 0;
		// 当前面值从0张开始尝试,直到大于对应的面值张数 或者 大于当前剩余金额
		for (int zhang = 0; zhang * coins[index] <= rest && zhang <= zhangs[index]; zhang++) {
			ways += process(coins, zhangs, index + 1, rest - (zhang * coins[index]));
		}

		return ways;
	}

动态规划

	public static int dp1(int[] arr, int aim) {
		if (arr == null || arr.length == 0 || aim < 0) {
			return 0;
		}
		info in = getInfo(arr);
		int[] coins = in.coins;
		int[] zhangs = in.zhangs;
		int n = coins.length;
		int[][] dp = new int[n + 1][aim + 1];
		dp[n][0] = 1;
		for (int index = n - 1; index >= 0; index--) {
			for (int rest = 0; rest <= aim; rest++) {
				int ways = 0;
				// 当前面值从0张开始尝试,直到大于对应的面值张数 或者 大于当前剩余金额
				for (int zhang = 0; zhang * coins[index] <= rest && zhang <= zhangs[index]; zhang++) {
					ways += dp[index + 1][ rest - (zhang * coins[index])];
				}
				dp[index][rest] = ways;
			}
		}
		return dp[0][aim];

	}

状态转移

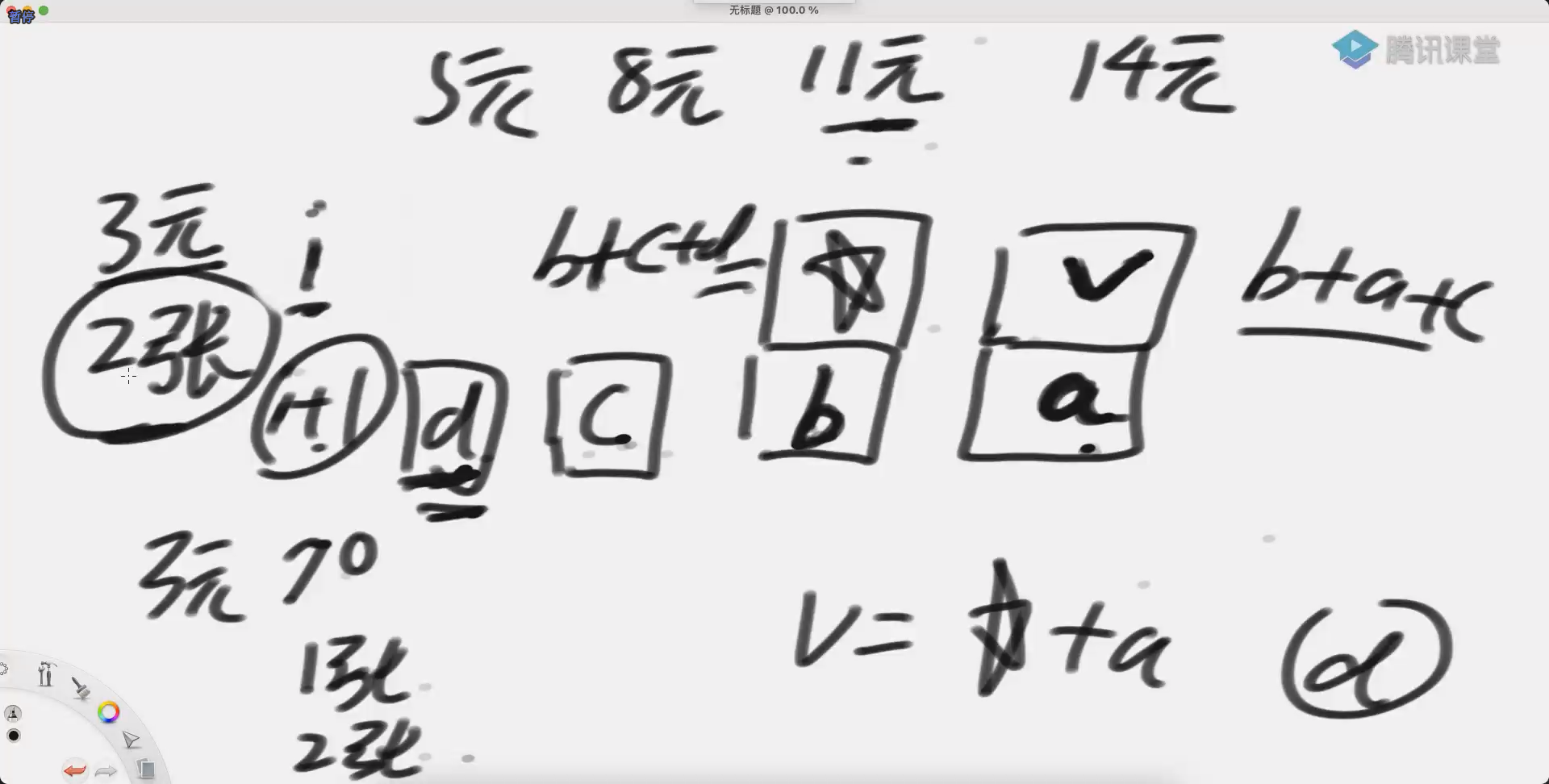
以 3 元面值货币 只有两张为例子

星号位置 (即 dp[index][rest - coins[index]] 位置) = dp[index+1][rest-0*coins[index]]+dp[index+1][rest-1*coins[index]]+dp[index+1][rest-2*coins[index]] = d+c+b

我们要当前位置结果为 dp[index][rest] = c+b+a

由于每个货币限制了张数 无法像完全背包问题那种完全依赖星号位置 即 dp[index][rest-arr[index]]+dp[index+1][rest] 得出当前结果

还是通过表依赖关系发现规律

星号位置只是多求了个 d 我们只需将 d 减去就可以得出结果 即 dp[index][rest-arr[index]]+dp[index+1][rest]-dp[index+1][rest-coins[index]*(zhang[index]+1)] 得出当前结果

	public static int dp2(int[] arr, int aim) {
		if (arr == null || arr.length == 0 || aim < 0) {
			return 0;
		}
		info info = getInfo(arr);
		int[] coins = info.coins;
		int[] zhangs = info.zhangs;
		int n = coins.length;
		int[][] dp = new int[n + 1][aim + 1];
		dp[n][0] = 1;
		for (int index = n - 1; index >= 0; index--) {
			for (int rest = 0; rest <= aim; rest++) {
				// 0张时
				dp[index][rest] = dp[index + 1][rest];
				// 继承它前面的状态 即星号位置
				if (rest - coins[index] >= 0) {
					dp[index][rest] += dp[index][rest - coins[index]];
				}
				// 减去d位置
				if (rest - coins[index] * (zhangs[index] + 1) >= 0) {
					dp[index][rest] -= dp[index + 1][rest - coins[index] * (zhangs[index] + 1)];
				}
			}
		}
		return dp[0][aim];
	}

醉汉存活率

给定5个参数，N，M，row，col，k
表示在N*M的区域上，醉汉Bob初始在(row,col)位置
Bob一共要迈出k步，且每步都会等概率向上下左右四个方向走一个单位
任何时候Bob只要离开N*M的区域，就直接死亡
返回k步之后，Bob还在N*M的区域的概率

暴力递归

	// 求存活率 存活次数/4^k
	public static double livePosibility1(int row, int col, int k, int N, int M) {
		return (double) process(row, col, k, N, M) / Math.pow(4, k);
	}

	/**
	 * 
	 * @param row  当前醉汉在(row,col)位置
	 * @param col
	 * @param rest 剩余步数
	 * @param n    n*m的区域
	 * @param m
	 * @return
	 */
	public static long process(int row, int col, int rest, int n, int m) {
		// 越界直接死亡 返回次数0
		if (row < 0 || row == n || col < 0 || col == m) {
			return 0;
		}
		// 剩余步数为0 并且还在区域中 直接返回1次
		if (rest == 0) {
			return 1;
		}
		// 4个方向尝试
		long left = process(row, col - 1, rest - 1, n, m);
		long right = process(row, col + 1, rest - 1, n, m);
		long down = process(row - 1, col, rest - 1, n, m);
		long up = process(row + 1, col, rest - 1, n, m);
		return left + right + down + up;
	}

动态规划

	public static double livePosibility2(int row, int col, int k, int n, int m) {
		long[][][] dp = new long[n][m][k + 1];

        //base case2
		for (int i = 0; i < n; i++) {
			for (int j = 0; j < m; j++) {
				dp[i][j][0] = 1;
			}
		}

		for (int rest = 1; rest <= k; rest++) {
			for (int r = 0; r < n; r++) {
				for (int c = 0; c < m; c++) {
					// 4个方向
					dp[r][c][rest] = pick(dp, n, m, r - 1, c, rest-1);
					dp[r][c][rest] += pick(dp, n, m, r + 1, c, rest-1);
					dp[r][c][rest] += pick(dp, n, m, r, c - 1, rest-1);
					dp[r][c][rest] += pick(dp, n, m, r, c + 1, rest-1);
				}
			}
		}

		return (double) dp[row][col][k] / Math.pow(4, k);
	}

	// 防止越界
	public static long pick(long[][][] dp, int n, int m, int r, int c, int rest) {
		if (r < 0 || r == n || c < 0 || c == m) {
			return 0;
		}
		return dp[r][c][rest];
	}

砍怪兽

给定3个参数，N，M，K
怪兽有N滴血，等着英雄来砍自己
英雄每一次打击，都会让怪兽流失[0~M]的血量
到底流失多少？每一次在[0~M]上等概率的获得一个值
求K次打击之后，英雄把怪兽砍死的概率

暴力递归

	//求概率
	public static double  right(int n ,int m ,int k) {
		if(n<1 || m <1 || k <1) {
			return 0;
		}
		//所有次数 (m+1)^k
		long all = (long)Math.pow(m+1, k);
		//杀死怪兽的总次数
		long kill = process(k,m,n);
		return (double) ((double) kill / (double) all);
	}

	/**
	 * 求杀死怪兽的总次数
	 * @param times 剩余打击次数
	 * @param m 0~m等概率的伤害
	 * @param hp 怪兽剩余血量
	 * @return
	 */
	public static long process(int times, int m, int hp ) {
		//打击次数剩余0
		if(times == 0) {
			//hp小于等于0返回击杀1次 否则返回0
			return hp <= 0 ? 1: 0;
		}
		//当前怪兽血量为小于0 为负数 直接用公式求出剩下的击杀次数 因为下面开始击杀怪兽已经死了  (m+1)^times
		if(hp < 0) {
			return (long)Math.pow(m+1, times);
		}
		long ways =0;
		for (int i = 0; i <=m; i++) {
			ways +=process(times-1, m, hp-i);
		}
		return ways;
	}

动态规划

	/**
	 * 
	 * @param n 怪兽多少滴血
	 * @param m 0~m等概率的伤害
	 * @param k 打击次数
	 * @return
	 */
	public static double dp1(int n, int m, int k) {
		if (n < 1 || m < 1 || k < 1) {
			return 0;
		}
		// 所有次数 (m+1)^k
		long all = (long) Math.pow(m + 1, k);
		long[][] dp = new long[k + 1][n + 1];
		// 剩打击次数0 并且怪兽0滴血 没有负数注意越界问题 base case1 return hp <= 0 ? 1 : 0;
		dp[0][0] = 1;
		//打击次数
		for (int times = 1; times <= k; times++) {
			// base case2 当怪兽血量小于等于0时 直接用公式求出次数
			dp[times][0] = (long) Math.pow(m + 1, times);
			//血量
			for (int hp = 1; hp <= n; hp++) {
				long ways = 0;
				//伤害 0~m范围
				for (int i = 0; i <= m; i++) {
					//如果当前血量-i后大于等于0 则继承它依赖的位置
					if (hp - i >= 0) {
						ways += dp[times - 1][hp - i];
					} else {
						//小于0 即当前血量被砍后为负数 用公式算 (m+1)^times-1
						ways += (long) Math.pow(m + 1, times - 1);
					}
				}
				dp[times][hp]=ways;
			}
		}

		long kill = dp[k][n];
		return (double) ((double) kill / (double) all);

	}

斜率优化

假设 m=3 我们求 dp[5][10]=dp[4][10]+dp[4][9]+...+dp[4][10-m]

如果 m=7

得出 dp[5][10]=dp[4][10]+...+dp[4][10-m]

所以我们无需重新再算了一次 dp[4][11]+...+dp[4][11-7] 直接状态转移 dp[5][10]

得出 dp[5][11] =dp[5][10]+dp[4][11]-dp[4][3]

根据以上依赖规律得出代数方程

dp[times][hp] = dp[times][hp - 1] + dp[times - 1][hp];
if (hp - 1 - m >= 0) {
    dp[times][hp] -= dp[times - 1][hp - 1 - m];
}

但是上面没有分析血量较少 不够减的情况 因为 if (hp - 1 - m >= 0) 只判断当前是否越界 (即血量在正数范围) 而会出现负数血量的情况 没有作处理

如当 m=5 dp[3][4] = dp[3][3] + dp[2][4] - dp[2][-2]

即 if (hp - 1 - m >= 0) 不成立没有减去 dp[times][hp] -= dp[times - 1][hp - 1 - m] ，由于我们开的是 k+1 行 n+1 列的表 无法取得负数 (即超过表的范围) 的情况

但我们可以使用公式来进行取得

$$(m+1{)}^{t}imes$$

for (int hp = 1; hp <= n; hp++) {
    dp[times][hp] = dp[times][hp - 1] + dp[times - 1][hp];
    if (hp - 1 - m >= 0) {
        dp[times][hp] -= dp[times - 1][hp - 1 - m];
    } else {
        dp[times][hp] -= (long) Math.pow(m + 1, times - 1);
    }
}

完整代码

	/**
	 * 
	 * @param n 怪兽多少滴血
	 * @param m 0~m等概率的伤害
	 * @param k 打击次数
	 * @return
	 */
	public static double dp2(int n, int m, int k) {
		if (n < 1 || m < 1 || k < 1) {
			return 0;
		}
		// 所有次数 (m+1)^k
		long all = (long) Math.pow(m + 1, k);
		long[][] dp = new long[k + 1][n + 1];
		// 剩打击次数0 并且怪兽0滴血 没有负数注意越界问题 base case1 return hp <= 0 ? 1 : 0;
		dp[0][0] = 1;
		// 打击次数
		for (int times = 1; times <= k; times++) {
			// base case2 当怪兽血量小于等于0时 直接用公式求出次数
			dp[times][0] = (long) Math.pow(m + 1, times);
			// 血量
			for (int hp = 1; hp <= n; hp++) {
				dp[times][hp] = dp[times][hp - 1] + dp[times - 1][hp];
				if (hp - 1 - m >= 0) {
					dp[times][hp] -= dp[times - 1][hp - 1 - m];
				} else {
					dp[times][hp] -= (long) Math.pow(m + 1, times - 1);
				}
			}
		}

		long kill = dp[k][n];
		return (double) ((double) kill / (double) all);

	}

最少货币

322. 零钱兑换 (opens new window)

arr是面值数组，其中的值都是正数且没有重复。再给定一个正数aim。
每个值都认为是一种面值，且认为张数是无限的。
返回组成aim的最少货币数

暴力递归

	public static int minCoins(int[] arr, int aim) {
		return process(arr, 0, aim);
	}

	/**
	 * 
	 * @param arr   货币面值数组
	 * @param index 当前面值位置
	 * @param rest  组成aim还剩多少
	 * @return 返回组成aim的最少货币数
	 */
	public static int process(int[] arr, int index, int rest) {
		// 没有货币
		if (index == arr.length) {
			// rest剩下的钱为0元时 返回0表示能凑够aim 否则返回int最大值表示无法凑够aim
			return rest == 0 ? 0 : Integer.MAX_VALUE;
		}
		int ans = Integer.MAX_VALUE;
		for (int zhang = 0; zhang * arr[index] <= rest; zhang++) {
			// 从0~zhang* arr[index] <=rest范围内选取zhang个货币arr[index]面值
			int next = process(arr, index + 1, rest - (zhang * arr[index]));
			// 如果返回的是integer.MAX_VALUE则说明当前zhang数张货币面值无法凑到aim
			if (next != Integer.MAX_VALUE) {
				// 更新最小值
				ans = Math.min(ans, zhang + next);
			}
		}
		return ans;

	}

动态规划

	public static int dp1(int[] arr, int aim) {
		if (aim == 0) {
			return 0;
		}
		int n = arr.length;
		int[][] dp = new int[n + 1][aim + 1];
		// base case 1
		dp[n][0] = 0;
		for (int i = 1; i <= aim; i++) {
			// base case1
			dp[n][i] = Integer.MAX_VALUE;
		}
		for (int index = n - 1; index >= 0; index--) {
			for (int rest = 0; rest <= aim; rest++) {
				int ans = Integer.MAX_VALUE;
				for (int zhang = 0; zhang * arr[index] <= rest; zhang++) {
					// 从0~zhang* arr[index] <=rest范围内选取zhang个货币arr[index]面值
					int next = dp[index + 1][rest - (zhang * arr[index])];
					// 如果返回的是integer.MAX_VALUE则说明当前zhang数张货币面值无法凑到aim
					if (next != Integer.MAX_VALUE) {
						// 更新最小值
						ans = Math.min(ans, zhang + next);
					}
				}
				dp[index][rest] = ans;
			}
		}
		return dp[0][aim];
	}

斜率优化

假设当前面值为 3 元货币 需要求当前位置 v = min( a+0 , b+1 , c+1 , d+3 , e+4 ...[直到 rest 小于 0 时停 因为是无限张])

而 v 前一个 x =min( b+0 , c+1 , d+2 , e+3 ...)

∴ v =min( x+1 , a+0 )

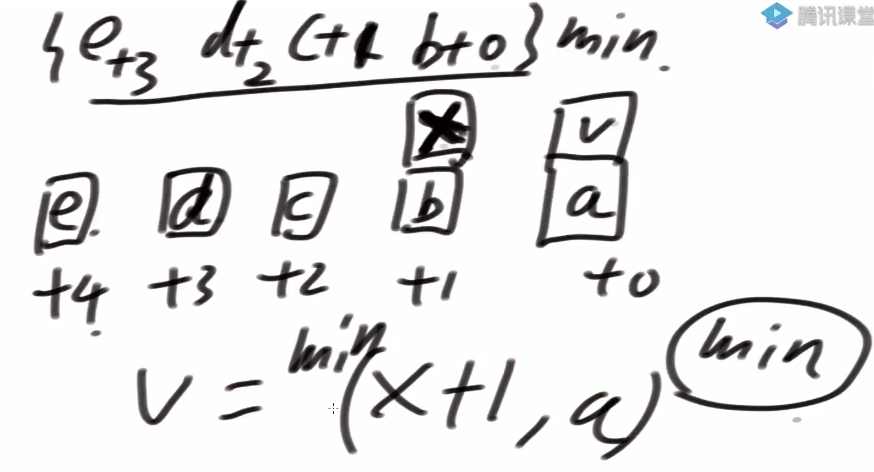
	public static int dp2(int[] arr, int aim) {
		if (aim == 0) {
			return 0;
		}
		int n = arr.length;
		int[][] dp = new int[n + 1][aim + 1];
		// base case 1
		dp[n][0] = 0;
		for (int i = 1; i <= aim; i++) {
			// base case1
			dp[n][i] = Integer.MAX_VALUE;
		}
		for (int index = n - 1; index >= 0; index--) {
			for (int rest = 0; rest <= aim; rest++) {
				// a+0
				dp[index][rest] = dp[index + 1][rest];
				//rest - arr[index] >= 0不越界(即在表的范围内)  
				//dp[index][rest - arr[index]] != Integer.MAX_VALUE 没有被标记为无法凑够的
				if (rest - arr[index] >= 0 && dp[index][rest - arr[index]] != Integer.MAX_VALUE) {
					dp[index][rest] = Math.min(dp[index][rest], dp[index][rest - arr[index]] + 1);
				}

			}
		}
		return dp[0][aim];
	}

何为斜率优化

如下图 两个格子有包含部分 我们可以看到两条线斜率相等 即可以使用斜率优化来优化一部分重复计算的过程如果 dp 中枚举行为

如果两格子斜率不相同 只有少部分包含关系 无法优化太多 如下图所示

如下图所示 可以尝试区间优化

空间压缩

完全背包（一维优化） 显然朴素版的完全背包进行求解复杂度有点高。

我们从最朴素背包转移方程出发，从数学的角度去推导一维优化是如何来的。

这十分科学，而绝对严谨。

但每次都这样推导是十分耗时的。

因此，我们这次站在一个「更高」的角度去看「完全背包」问题。

我们知道传统的「完全背包」二维状态转移方程是：

$$f[i][j]=max(f[i-1][j],f[i-1][j-k\ast w[i]]+k\ast v[i])$$

经过一维空间优化后的状态转移方程是（同时容量维度遍历顺序为「从小到大」）：

$$f[j]=max(f[j],f[j-w[i]]+v[i])$$

这是我们在 学习完全背包 时推导的，是经过严格证明的，具有一般性的。

然后我们只需要对「成本」&「价值」进行抽象，并结合「换元法」即可得到任意背包问题的一维优化状态转移方程。

拿我们本题的状态转移方程来分析，本题的朴素状态转移方程为：

$$f[i][j]=min(f[i-1][j],f[i-1][j-k\ast coin]+k)$$

我们将硬币的面值抽象为「成本」，硬币的数量抽象「价值」，再对物品维度进行消除，即可得：

$$f[j]=min(f[j],f[j-coin]+1)$$

如果还不理解，可以将上述四个状态转移方程「两两成对」结合来看。

使用 0x3f3f3f3f 作为最大值，这样我们使用 INF 做状态转移的时候，就不需要先判断再使用了

而 0xbfbfbfbf 则是一个很小的负数（其实是太大了，超出了 int 的范围就变成了负数）。

    public int coinChange(int[] arr, int aim) {
		if (aim == 0) {
			return 0;
		}
		int n = arr.length;
        int INF = 0x3f3f3f3f; //魔法数 无限大的数 
		int[] dp = new int[aim + 1];
		// base case 1
		dp[0] = 0;
		for (int i = 1; i <= aim; i++) {
			// base case1
			dp[i] = INF;
		}
		for (int index = 1; index <= n; index++) {
			for (int rest = arr[index-1]; rest <= aim; rest++) {
				// a+0
				// dp[index][rest] = dp[index + 1][rest];
				//rest - arr[index] >= 0不越界(即在表的范围内)  
				//dp[index][rest - arr[index]] != Integer.MAX_VALUE 没有被标记为无法凑够的
				// if (rest - arr[index] >= 0 && dp[index][rest - arr[index]] != Integer.MAX_VALUE) {
				// 	dp[index][rest] = Math.min(dp[index][rest], dp[index][rest - arr[index]] + 1);
				// }
                dp[rest] =  Math.min(dp[rest], dp[rest - arr[index-1]] + 1);

			}
		}
		return dp[aim] == INF ? -1 : dp[aim];
    }

数字拆分

给定一个正数n，求n的裂开方法数，
规定：后面的数不能比前面的数小
比如4的裂开方法有：
1+1+1+1、1+1+2、1+3、2+2、4
5种，所以返回5

暴力递归

public static int ways(int n) {
		if (n < 0) {
			return 0;
		}
		if (n == 1) {
			return 1;
		}
		return process(1, n);
	}

	/**
	 * 
	 * @param pre  上一个拆出来的数为pre
	 * @param rest 还剩rest数值要拆
	 * @return
	 */
	public static int process(int pre, int rest) {
		// rest 为0 已经无法再拆
		if (rest == 0) {
			return 1;
		}
		// 上个拆出来的数 大于 rest 无法再拆出比pre大于等于的数 直接返回0次
		if (pre > rest) {
			return 0;
		}
        //pre < rest的情况
		int ways = 0;
		for (int first = pre; first <= rest; first++) {
			// 从pre~rest范围的数进行尝试
			ways += process(first, rest - first);
		}
		return ways;
	}

动态规划

通过 base case1 和 base case2 得出

		// rest 为0 已经无法再拆
		if (rest == 0) {
			return 1;
		}
		// 上个拆出来的数 大于 rest 无法再拆出比pre大于等于的数 直接返回0次
		if (pre > rest) {
			return 0;
		}

每个对角线的格子都是依赖本行的 0 列的值 即为 1

	public static int dp1(int n) {
		if (n < 0) {
			return 0;
		}
		if (n == 1) {
			return 1;
		}
		int[][] dp = new int[n + 1][n + 1];
		for (int pre = 1; pre <= n; pre++) {
			// 当rest 0时全为1次
			dp[pre][0] = 1;
			// 对角线
			dp[pre][pre] = 1;
		}
		// 0行不需要
		for (int pre = n - 1; pre >= 1; pre--) {
			for (int rest = pre + 1; rest <= n; rest++) {
				int ways = 0;
				for (int first = pre; first <= rest; first++) {
					// 从pre~rest范围的数进行尝试
					ways += dp[first][rest - first];
				}
				dp[pre][rest] = ways;
			}
		}
		return dp[1][n];

	}

斜率优化

通过上方 dp1 发现有枚举行为 尝试分析是否能够进行优化

通过具体例子分析 如: process(3,6)

△依赖着表中的 4 个□

而通过分析它的上下左右 发现它下方是有状态转移有利可图 继续通过具体例子分析 process(4,6)

得出 dp[4][6] = dp[6][0]+dp[5][1]+dp[4][2] 包含我们求 dp[3][6] 之中可以进行斜率优化

dp[pre][rest] = dp[pre+1][rest]+dp[pre][rest-pre]

	public static int dp2(int n) {
		if (n < 0) {
			return 0;
		}
		if (n == 1) {
			return 1;
		}
		int[][] dp = new int[n + 1][n + 1];
		for (int pre = 1; pre <= n; pre++) {
			// 当rest 0时全为1次
			dp[pre][0] = 1;
			// 对角线
			dp[pre][pre] = 1;
		}
		// 0行不需要
		for (int pre = n - 1; pre >= 1; pre--) {
			for (int rest = pre + 1; rest <= n; rest++) {
				// 当前位置底下的依赖
				dp[pre][rest] = dp[pre + 1][rest];
				// 左边格子
				dp[pre][rest] += dp[pre][rest - pre];

			}
		}
		return dp[1][n];

	}

拆分集合

给定一个正数数组arr，
请把arr中所有的数分成两个集合，尽量让两个集合的累加和接近
返回最接近的情况下，较小集合的累加和

暴力递归

	public static int right(int[] arr) {
		if (arr == null || arr.length < 2) {
			return 0;
		}
		int sum = 0;
		for (int num : arr) {
			sum += num;
		}
		return process(arr, 0, sum / 2);
	}

	/**
	 * 
	 * @param arr   数值集合
	 * @param index 当前集合元素位置
	 * @param rest  距离sum/2还有差多少
	 * @return 返回累加和尽量接近rest，但不能超过rest的情况下，最接近的累加和是多少
	 */
	public static int process(int[] arr, int index, int rest) {
		if (index == arr.length) {
			// 没有数可以选择了 直接返回0
			return 0;
		}
		// 还有数可以选择 index位置的数

		// 决策1 不使用当前位置的数
		int p1 = process(arr, index + 1, rest);
		// 决策2 使用当前的数
		int p2 = 0;
		// 判断当前位置的数 是否超过rest剩余数值
		if (arr[index] <= rest) {
			p2 = arr[index] + process(arr, index + 1, rest - arr[index]);
		}
		return Math.max(p1, p2);
	}

动态规划

通过具体例子查看是否有重复解出现 有重复解 改 dp 有利可图

通过 base case 得知 index== arr.length 时返回 0 即 n 行全为 0

并且每个位置依赖它的下一行

需要求的答案为 dp[0][sum/2]

	public static int dp(int[] arr) {
		if (arr == null || arr.length < 2) {
			return 0;
		}
		int sum = 0;
		for (int num : arr) {
			sum += num;
		}
		sum /= 2;
		int n = arr.length;
		int[][] dp = new int[n + 1][sum + 1];
//		if(index== arr.length) {
//			//没有数可以选择了 直接返回0
//			return 0;
//		}
		for (int index = n - 1; index >= 0; index--) {
			for (int rest = 0; rest <= sum; rest++) {
				// 决策1 不使用当前位置的数
				int p1 = dp[index + 1][rest];
				// 决策2 使用当前的数
				int p2 = 0;
				// 判断当前位置的数 是否超过rest剩余数值
				if (arr[index] <= rest) {
					p2 = arr[index] + dp[index + 1][rest - arr[index]];
				}
				dp[index][rest] = Math.max(p1, p2);
			}

		}
		return dp[0][sum];
	}

拆分集合 2

给定一个正数数组arr，请把arr中所有的数分成两个集合
如果arr长度为偶数，两个集合包含数的个数要一样多
如果arr长度为奇数，两个集合包含数的个数必须只差一个
请尽量让两个集合的累加和接近
返回最接近的情况下，较小集合的累加和

暴力递归

	public static int right(int[] arr) {
		if (arr == null || arr.length < 2) {
			return 0;
		}
		int sum = 0;
		for (int num : arr) {
			sum += num;
		}
		if ((arr.length & 1) == 0) {
			return process(arr, 0, arr.length / 2, sum / 2);
		} else {
			return Math.max(process(arr, 0, arr.length / 2, sum / 2), process(arr, 0, (arr.length + 1) / 2, sum / 2));
		}
	}

	/**
	 * 
	 * @param arr   数值数值
	 * @param index 当前数值位置
	 * @param picks 还需要选picks个
	 * @param rest  离rest即(sum/2)还剩下多少
	 * @return
	 */
	public static int process(int[] arr, int index, int picks, int rest) {
		// 没有数可以挑了
		if (index == arr.length) {
			// 判断是否选够picks个数 是返回0 否则返回-1用于标记无法凑够
			return picks == 0 ? 0 : -1;
		}
		// 决策1 不选取当前位置的数
		int p1 = process(arr, index + 1, picks, rest);
		// 决策2 选择当前位置的数
		int p2 = -1;
		int next = -1;
		// 当前选择的数 必须小于等于 剩下的值 否则会凑到rest变负数
		if (arr[index] <= rest) {
			next = process(arr, index + 1, picks - 1, rest - arr[index]);
		}
		// 如果选择当前的数 是可以凑够的则进行p2赋值
		if (next != -1) {
			p2 = arr[index] + next;
		}

		return Math.max(p1, p2);
	}

动态规划

根据 base case1 得知 当 index==n 并且 picks ==0 时返回 0 其他情况返回 - 1

而每一层依赖是它的下一层 我们把第 N 层填好即可进行求解

	public static int dp1(int[] arr) {
		if (arr == null || arr.length < 2) {
			return 0;
		}
		int sum = 0;
		for (int num : arr) {
			sum += num;
		}
		sum /= 2;
		int n = arr.length;
		int m = (n + 1) / 2;
		int[][][] dp = new int[n + 1][m + 1][sum + 1];
		// 初始化全为-1
		for (int i = 0; i <= n; i++) {
			for (int j = 0; j <= m; j++) {
				Arrays.fill(dp[i][j], -1);
//				for (int k = 0; k <=sum; k++) {
//					dp[i][j][k] = -1;
//				}
			}
		}

		// 根据base case 只有当index==n 并且picks为0时才返回0
		for (int rest = 0; rest <= sum; rest++) {
			dp[n][0][rest] = 0;
		}

		for (int index = n - 1; index >= 0; index--) {
			for (int picks = 0; picks <= m; picks++) {
				for (int rest = 0; rest <= sum; rest++) {
					// 决策1 不选取当前位置的数
					int p1 = dp[index + 1][picks][rest];
					// 决策2 选择当前位置的数
					int p2 = -1;
					int next = -1;
					// 当前选择的数 必须小于等于 剩下的值 否则会凑到rest变负数
					// 这里注意 picks-1会越界 需要提前判断一下
					if (arr[index] <= rest && picks - 1 >= 0) {
						next = dp[index + 1][picks - 1][rest - arr[index]];
					}
					// 如果选择当前的数 是可以凑够的则进行p2赋值
					if (next != -1) {
						p2 = arr[index] + next;
					}

					dp[index][picks][rest] = Math.max(p1, p2);
				}
			}
		}

动态规划总结

什么样的暴力递归可以优化？

有重复调用同一个子问题的解，这种递归可以优化

如果每一个子问题都是不同的解，无法优化也不用优化

暴力递归跟动态规划的关系

某一个暴力递归，有解的重复调用，就可以把这个暴力递归优化成动态规划

任何动态规划问题，都一定对应着某一个有解的重复调用的暴力递归

但不是所有的暴力递归，都一定对应着动态规划

面试题和动态规划的关系

解决一个问题，可能有很多尝试方法

可能在很多尝试方法中，又有若干个尝试方法有动态规划的方式

一个问题 可能有 若干种动态规划的解法

如何找到某个问题的动态规划方式？

1. 设计暴力递归：重要原则 + 4 种常见尝试模型！重点！
2. 分析有没有重复解：套路解决
3. 用记忆化搜索 -> 用严格表结构实现动态规划：套路解决
4. 看看能否继续优化：套路解决

面试中设计暴力递归过程的原则

1. 每一个可变参数的类型，一定不要比 int 类型更加复杂某个尝试，你的可变参数居然突破整形了，马上放弃这种猜法，换一个去猜
2. 原则 1 可以违反，让类型突破到一维线性结构，那必须是单一可变参数 => 对应的是贴纸问题，直接用单个可以，傻缓存解决
3. 如果发现原则 1 被违反，但不违反原则 2，只需要做到记忆化搜索即可
4. 可变参数的个数，能少则少 一个可变参数：一维表 两个可变参数：二维表 三个可变参数：三维表

常见的 4 种尝试模型

1. 从左往右的尝试模型
2. 范围上的尝试模型
3. 样本对应的尝试模型
4. 寻找业务限制的尝试模型

暴力递归到动态规划的套路

1. 你已经有了一个不违反原则的暴力递归，而且的确存在解的重复调用 有重复解，可优化

2. 找到哪些参数的变化会影响返回值，对每一个列出变化范围

   寻找可变参数的变化范围

3. 参数间的所有的组合数量，意味着表大小

   根据变化范围 创建表的大小

4. 记忆化搜索的方法就是傻缓存，非常容易得到

   简单记忆化搜索

5. 规定好严格表的大小，分析位置的依赖顺序，然后从基础填写到最终解

   根据具体案例 分析表依赖

6. 对于有枚举行为的决策过程，进一步优化

   有枚举行为 尝试是否能够斜率优化

动态规划的进一步优化

1. 空间压缩
2. 状态化简
3. 动态规划中的四边形不等式优化

其他优化技巧略

N 皇后问题

N皇后问题是指在N*N的棋盘上要摆N个皇后，
要求任何两个皇后不同行、不同列， 也不在同一条斜线上
给定一个整数n，返回n皇后的摆法有多少种。n=1，返回1
n=2或3，2皇后和3皇后问题无论怎么摆都不行，返回0
n=8，返回92

暴力递归

	public static int num1(int n) {
		if (n < 1) {
			return 0;
		}
		int[] record = new int[n];
		return process1(0, record, n);
	}

	/**
	 * 
	 * @param i      当前来到i行
	 * @param record 记录每行的皇后存放在哪一列 如下标0为2 说明第一行的皇后放在第三列 即record[x] = y 说明第x行的皇后放在第y列
	 * @param n      一共有多少行
	 * @return
	 */
	public static int process1(int i, int[] record, int n) {
		// 已经放过n行了 即n个皇后都放置了
		if (i == n) {
			return 1;
		}
		int res = 0;
		// i行的皇后 可以放在当前i行的哪一列
		for (int j = 0; j < n; j++) {
			if (isValid(record, i, j)) {
				// 当前位置合法 记录位置
				// record 数组不需要回溯 判断时只会遍历它本行的前面位置 并且每次会覆盖
				record[i] = j;
				res += process1(i + 1, record, n);
			}
		}
		return res;
	}

	/**
	 * 判断当前皇后可以放置在哪一列合法
	 * 
	 * @param record 记录的皇后位置列的数组
	 * @param i      当前行
	 * @param j      当前列
	 * @return
	 */
	public static boolean isValid(int[] record, int i, int j) {
		// 只遍历它前面行的 皇后存储的位置
		for (int k = 0; k < i; k++) {
			// 同列 不可以存储当前位置
			if (j == record[k]) {
				return false;
			}
			// 在同一斜线上 不能放置
			if (Math.abs(record[k] - j) == Math.abs(i - k)) {
				return false;
			}
		}
		return true;
	}

使用 int 存储位运算的暴力解法

n 皇后的时间复杂程度

该方法是使用 int 的 32 位来存储每个皇后的状态

所以只能求 1~32 的皇后问题 无法求出 33 及以上皇后的问题

使用 3 个 int 存储 列 左下对角线和右下对角线的状态 当前行根据前个皇后传递的状态 3 个 int 状态 快速筛选能够进行尝试的位置

将 3 个 int 进行或运算 然后做相反数操作 与 原数作与运算 得出最右侧的 1

提取最右的 1

红色方框中的 1 为当前行皇后可以进行尝试的列位置

	public static int num2(int n ) {
		//无法求出33及以上的皇后问题
		if(n < 1 || n> 32) {
			return 0;
		}
		//如是8皇后问题则 最右的8个位都是1 用1存储皇后
		int limit  = n == 32 ? -1 : (1<< n )-1 ;
		return process2(limit,0,0,0);
	}
	
	/**
	 * 
	 * @param limit  多少位皇后问题
	 * @param colLim  列皇后存储状态
	 * @param leftDiaLim  左下对角线存储状态
	 * @param rightDiaLim  右下对角线存储状态
	 * @return
	 */
	public static int process2(int limit, int colLim, int leftDiaLim, int rightDiaLim) {
		//全部列都放满了 返回1次
		if(colLim == limit) {
			return 1;
		}
		//pos中所有1的位置 是可以去尝试的问题
		//colLim | leftDiaLim | rightDiaLim 代表左下对角线、右下角对角线和列 合法的位置 1为存在之前会造成违规的皇后  0为可以尝试的位置
		//再取反~(colLim | leftDiaLim | rightDiaLim) 说明为1的位置是可以尝试放置的位置 0为会违法
		//与limit作与运算 变成 0为合法 1为违法
		int pos = limit & (~(colLim | leftDiaLim | rightDiaLim));
		int mostRightOne = 0;
		int res = 0;
		while(pos != 0) {
			//提前最右侧的1 (~pos +1) 为负数数
			//再与pos作与运算 得出最右侧的1
			mostRightOne =  pos & (~pos +1);
			//System.out.println(~-3+1); //3
			//System.out.println(~3+1); //-3
			//System.out.println(3 & (~3+1)); //1
			pos = pos -mostRightOne; //去掉已经尝试过的皇后
			res += process2(limit, 
					colLim | mostRightOne, //记录当前被使用的列
					(leftDiaLim | mostRightOne) << 1, //左下对角线 因为记录的是当前行 而下一行需要左移一位 
					(rightDiaLim | mostRightOne) >>> 1); //右下对角线 右移一位
		}
		return res;
	}